Introduction
N-ary trees are tree data structures that allow us to have up to n children nodes for each of the nodes, differing from the standard binary trees which allow only up to 2 children nodes for each node.
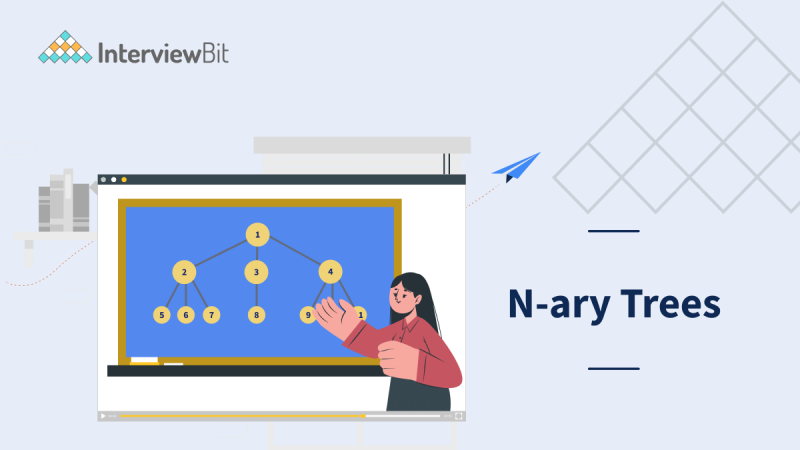
The above picture shows an example of an n-ary tree. Observe that in the example, the tree has a total of n = 11 nodes, where some nodes have 3 children, some have only 1 child, and some don’t have any children at all. This tree is an N-ary tree where N >= 3 because the number of children of the tree ranges from 0 to 3.
1. Naive Approach
We basically need to store 2 pieces of information to completely represent an N-ary tree.
- The value of the node
- The addresses of all its children nodes.
We can build a class or struct to store this information effectively. For storing the latter information, we can use an Array or LinkedList. Both these data structures will however have some shortcomings which we will discuss below:
- Since the number of children of a node is not known beforehand, we can store only a fixed number of children’s addresses in an array.
- LinkedList won’t allow us to randomly access any child’s address, so it will be expensive in terms of complexity.
2. Improved Approach
To improve the shortcomings of the naive approach, we can use Dynamic Arrays to store the addresses of the children of the nodes. Using this approach, we can randomly access any child’s address in O(1) as well as don’t have to know the number of children of each node beforehand.
Sample Implementation
class TreeNode {
int value;
vector<TreeNode*> children;
};
3. Optimal Approach
The optimal way to implement a Node for an N-ary Tree will be to use the First Child/Next Sibling representation. The steps to implement this are as follows:
- For each node, we link the children of the common parent(siblings) from left to right order.
- Then we will remove the links from the parent to all the children, except for the first child node.
The focus of this representation is that since we have a link between children, we do not need extra links from parents to all the children.
Advantages
- Since no extra links are required, we can consider this to be a memory-efficient implementation.
- All the nodes are of constant size, and no dynamic arrays or linked lists are required.
- With the above representation, we can convert all n-ary trees into a binary tree representation, which is a topic we are more familiar with.
- Many algorithms can be expressed and implemented more easily because we can consider the N-ary tree to be a binary tree.
Sample Implementation
struct TreeNode {
int value;
TreeNode* firstChild;
TreeNode* nextSibling;
};