Pattern Search – KMP Algorithm

Problem Statement

The Pattern Searching algorithms are also called String Matching Algorithms. These algorithms are very helpful in the case of searching a string within another string.

Given a text str[0..n-1] and a pattern pat[0..m-1], write a program with a function PatternSearch(char pat[], char str[]) that prints all occurrences of pat[] in str[]. Given that n > m.

Examples:

Input: str[] = “THIS IS A TEXT”
pat[] = “TEXT”

Output: Pattern found at index 10.

Naive Approach

In this approach, we will check each and every substring of the string. Below are the steps to follow.

• Iterate over the string for i from 0 to n – 1 (n is the size of the string).
• For every value of i slide the pattern over the text one by one and check for a match. If there is a match, then slides by 1 again to check for subsequent matches.

Dry Run of Naive Approach For Pattern Search

C Implementation

void Patternsearch(char* pat, char* str) {
    int M = strlen(pat);
    int N = strlen(str);
    for (int i = 0; i <= N - M; i++) {
        int j;
 
        for (j = 0; j < M; j++)
            if (str[i + j] != pat[j])
                break;
 
        if (j == M)
            printf("Pattern found at index %d \n", i);
    }
}

Java Implementation

public static void Patternsearch(String str, String pat) {
  int M = pat.length();
  int N = str.length();

  for (int i = 0; i <= N - M; i++) {

    int j;
    for (j = 0; j < M; j++)
      if (str.charAt(i + j) != pat.charAt(j))
        break;

    if (j == M)
      System.out.println("Pattern found at index " + i);
  }
}

Python Implementation

def Patternsearch(pat, str):
    M = len(pat)
    N = len(str) 
    for i in range(N - M + 1):
        j = 0
        while(j < M):
            if (str[i + j] != pat[j]):
                break
            j += 1
 
        if (j == M):
            print("Pattern found at index ", i)

• Time Complexity: O(n) in the Best case and O(m*(n-m+1)) in the worst case.
• Space Complexity: O(1).

KMP Pattern Searching

The KMP calculation utilizes the deteriorating property (design having the same sub-designs showing up more than once in the example) of the example and further develops the most pessimistic scenario running time complexity to O(n). The thought for the KMP calculation is: at whatever point the string gets mismatched, we definitely know a portion of the characters in the text of the following window. We will exploit this data to try not to coordinate with the characters that we realize will coordinate.

• The KMP algorithm pre-computes pat[] and creates an array lps[] of size m (same as the size of pattern) which is used to jump characters while matching.
• We search for lps in sub-patterns. More commonly we focus on sub-strings of patterns that are either prefixes and suffixes.
• For every sub-pattern pat[0..i] where i range from 0 to m-1, lps[i] stores the size of the maximum matching proper prefix which is also a suffix of the sub-pattern pat[0..i].

How can we utilize lps[] to decide the next positions or to know the number of characters to be jumped?

• We begin contrasting pat[j] with j = 0 with characters of the current window of text.
• We keep checking characters str[i] and pat[j] and keep incrementing i and j while pat[j] and str[i] keep matching.
• When we see there is a mismatch then,
  • It is already known that characters pat[0..j-1] are the same as str[i-j…i-1]
  • From the above points, we can conclude that lps[j-1] is the frequency of characters of pat[0…j-1] that are both proper prefixes and proper suffixes.
  • In conclusion, we don’t need to check these lps[j-1] characters with str[i-j…i-1] because we know that these characters will always match.

Dry Run Of the Above Approach

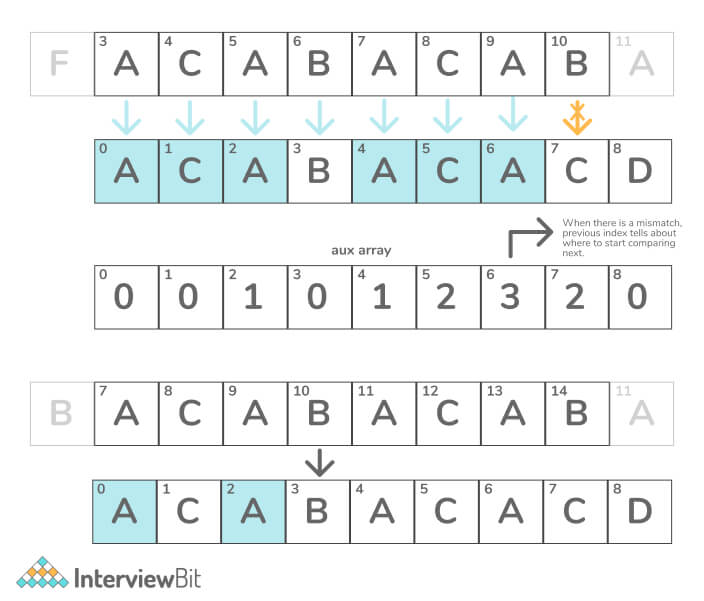
C++ Implementation of KMP

void KMPStringSearch(char* pat, char* str) {
    int M = strlen(pat);
    int N = strlen(str);
  
    int lps[M];
    computeLPSArray(pat, M, lps);
  
    int i = 0; 
    int j = 0;
    while (i < N) {
        if (pat[j] == str[i]) {
            j++;
            i++;
        }
  
        if (j == M) {
            printf("Found pattern at index %d ", i - j);
            j = lps[j - 1];
        }
        else if (i < N && pat[j] != str[i]) {
            if (j != 0)
                j = lps[j - 1];
            else
                i = i + 1;
        }
    }
}
  
void computeLPSArray(char* pat, int M, int* lps) {
        int len = 0;
  
    lps[0] = 0;   
       int i = 1;
    while (i < M) {
        if (pat[i] == pat[len]) {
            len++;
            lps[i] = len;
            i++;
        }
        else{
           if (len != 0) {
                len = lps[len - 1];
           }
            else             {
                lps[i] = 0;
                i++;
            }
        }
    }
}

Java Implementation of KMP

void KMPStringSearch(String pat, String str) {
  int M = pat.length();
  int N = str.length();

  int lps[] = new int[M];
  int j = 0; // index for pat[]

  computeLPSArray(pat, M, lps);

  int i = 0;
  while (i < N) {
    if (pat.charAt(j) == str.charAt(i)) {
      j++;
      i++;
    }
    if (j == M) {
      System.out.println("Found pattern " +
        "at index " + (i - j));
      j = lps[j - 1];
    } else if (i < N && pat.charAt(j) != str.charAt(i)) {

      if (j != 0)
        j = lps[j - 1];
      else
        i = i + 1;
    }
  }
}

void computeLPSArray(String pat, int M, int lps[]) {
  int len = 0;
  int i = 1;
  lps[0] = 0; // lps[0] is always 0

  while (i < M) {
    if (pat.charAt(i) == pat.charAt(len)) {
      len++;
      lps[i] = len;
      i++;
    } else {

      if (len != 0) {
        len = lps[len - 1];

      } else {
        lps[i] = len;
        i++;
      }
    }
  }
}

Python Implementation of KMP

def KMPStringSearch(pat, st):
    M = len(pat)
    N = len(st)
  
   
    lps = [0]*M
    j = 0 
  
    computeLPSArray(pat, M, lps)
  
    i = 0     
    while i < N:
        if pat[j] == st[i]:
            i += 1
            j += 1
  
        if j == M:
            print ("Found pattern at index " + str(i-j))
            j = lps[j-1]
  
        
        elif i < N and pat[j] != st[i]:
            

            if j != 0:
                j = lps[j-1]
            else:
                i += 1
  
def computeLPSArray(pat, M, lps):
    len = 0 
  
    lps[0] 
    i = 1
  
    
    while i < M:
        if pat[i]== pat[len]:
            len += 1
            lps[i] = len
            i += 1
        else:
            
            if len != 0:
                len = lps[len-1]
            else:
                lps[i] = 0
                i += 1

Time Complexity: O(n) in the worst case where n is the length of text.
Space Complexity: O(m) where m is the size of the pattern.

Practice Questions

Regular Expression Match
Regular Expression II

Frequently Asked Questions

Q.1: Which of the above approaches is better with respect to space complexity?

Ans: The brute or simple approach is better if we only consider the space complexity.

Q.2: Are there any other pattern-matching algorithms?

Ans: Yes, Rabin Karp algorithm, Boyer Moore algorithm, etc.