Merge Two Sorted Arrays

Problem Statement

Given two sorted arrays A[] and B[] of size N and M. The task is to merge both the arrays into a single array in non-decreasing order.

Examples:

Input: A[] =[3, 9, 10, 18, 23], B[] = [5, 12, 15, 20, 21, 25]
Output: [3, 5, 9, 10, 12, 15, 18, 20, 21, 23, 25]
Explanation: The merged array contains all the elements from both arrays in sorted order.

Input:  A[] = [1, 5], B[] = [4, 6, 7]
Output: [1, 4, 5, 6, 7]

Insert and Sort Approach

The most naive approach is to simply merge elements of one array into another and sort the resultant array.

C++ Code

  void merge(int nums1[], int m, int nums2[], int n) {
        for (int i = 0; i < n; i++) {
            nums1[i + m] = nums2[i];
        }
        sort(nums1, nums1 + n + m);
    }

Java Code

public void merge(int[] nums1, int m, int[] nums2, int n) {
        for (int i = 0; i < n; i++) {
            nums1[i + m] = nums2[i];
        }
        Arrays.sort(nums1);
    }

Python Code

def merge(nums1, m, nums2, n)
        for i in range(n):
            nums1[i + m] = nums2[i]
        
        nums1.sort()

Time Complexity:O((N + M)log(N+M)), where N and M are the size of array A[] and B[]
Space Complexity:O(N), built-in sort takes space

Merge Sort Method

The key idea to note here is that both the arrays are sorted. Therefore, taking advantage of this fact, we can apply a method similar to the merge sort technique.
Create an auxiliary array of size N + M and insert the merge element in this array.

Let us understand this approach with an example:

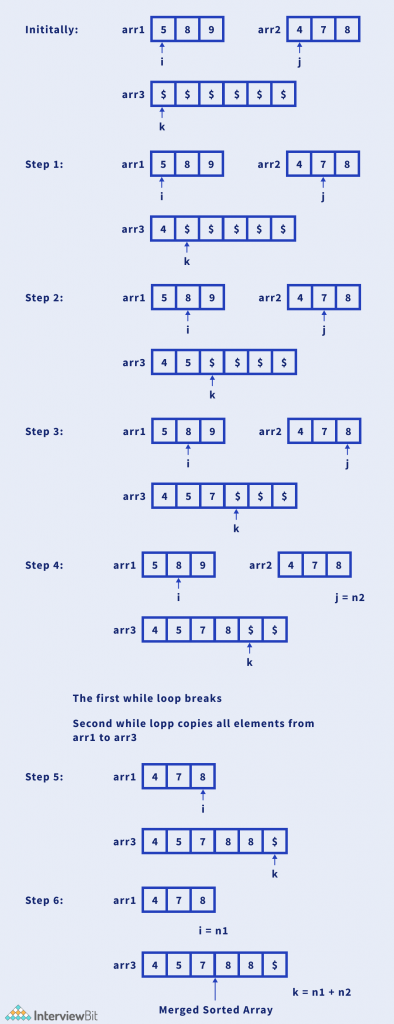
Algorithm

• Create an auxiliary array of size N + M.
• Put two pointers i and j and initialise them to 0. 
• Pointer i points to the first array, whereas pointer j points to the second array.
• Traverse both the array simultaneously using the pointers, and pick the smallest elements among both the array and insert in into the auxiliary array.
• Increment the pointers.
• After traversal, return the merged array.

C++ Implementation

void mergeArrays(int arr1[], int arr2[], int n1,
  int n2, int arr3[]) {
  int i = 0, j = 0, k = 0;
  while (i < n1 && j < n2) {
    if (arr1[i] < arr2[j])
      arr3[k++] = arr1[i++];
    else
      arr3[k++] = arr2[j++];
  }
  while (i < n1)
    arr3[k++] = arr1[i++];
 
  while (j < n2)
    arr3[k++] = arr2[j++];
}

Java Implementation

public static void mergeArrays(int[] arr1, int[] arr2, int n1,
  int n2, int[] arr3) {
  int i = 0, j = 0, k = 0;
  while (i < n1 && j < n2) {
    if (arr1[i] < arr2[j])
      arr3[k++] = arr1[i++];
    else
      arr3[k++] = arr2[j++];
  }
  while (i < n1)
    arr3[k++] = arr1[i++];
 
  while (j < n2)
    arr3[k++] = arr2[j++];
}

Python Implementation

def mergeArrays(arr1, arr2, n1, n2):
    arr3 = [None] * (n1 + n2)
    i = 0
    j = 0
    k = 0
 
    while i < n1 and j < n2:
        if arr1[i] < arr2[j]:
            arr3[k] = arr1[i]
            k = k + 1
            i = i + 1
        else:
            arr3[k] = arr2[j]
            k = k + 1
            j = j + 1
 
    while i < n1:
        arr3[k] = arr1[i]
        k = k + 1
        i = i + 1
 
    while j < n2:
        arr3[k] = arr2[j]
        k = k + 1
        j = j + 1

Time Complexity:O(N + M), where N and M is the size of array A[] and B[]
Space Complexity:O(N + M), as the auxiliary array is used

FAQs

How is the space complexity O(1) for the two-pointers approach?
Since, we are in placing merging all the elements into the first array, without creating any other auxiliary space, the space complexity is O(1)

How is the two pointer approach different from the merge sort approach?
The merge sort approach considers an auxiliary array to sort and keeps two-pointer and the beginning of the array and merges accordingly.

Whereas, the two-pointer approach, starts iterating from backward and keeps merging the elements in place.