Problem Statement
Given two sorted arrays A[] and B[] of size N and M. The task is to merge both the arrays into a single array in non-decreasing order.
Examples:
Input: A[] =[3, 9, 10, 18, 23], B[] = [5, 12, 15, 20, 21, 25]
Output: [3, 5, 9, 10, 12, 15, 18, 20, 21, 23, 25]
Explanation: The merged array contains all the elements from both arrays in sorted order.
Confused about your next job?
Input: A[] = [1, 5], B[] = [4, 6, 7]
Output: [1, 4, 5, 6, 7]
Insert and Sort Approach
The most naive approach is to simply merge elements of one array into another and sort the resultant array.
C++ Code
void merge(int nums1[], int m, int nums2[], int n) {
for (int i = 0; i < n; i++) {
nums1[i + m] = nums2[i];
}
sort(nums1, nums1 + n + m);
}Java Code
public void merge(int[] nums1, int m, int[] nums2, int n) {
for (int i = 0; i < n; i++) {
nums1[i + m] = nums2[i];
}
Arrays.sort(nums1);
}Python Code
def merge(nums1, m, nums2, n)
for i in range(n):
nums1[i + m] = nums2[i]
nums1.sort()Time Complexity:O((N + M)log(N+M)), where N and M are the size of array A[] and B[]
Space Complexity:O(N), built-in sort takes space
Merge Sort Method
The key idea to note here is that both the arrays are sorted. Therefore, taking advantage of this fact, we can apply a method similar to the merge sort technique.
Create an auxiliary array of size N + M and insert the merge element in this array.
Let us understand this approach with an example:
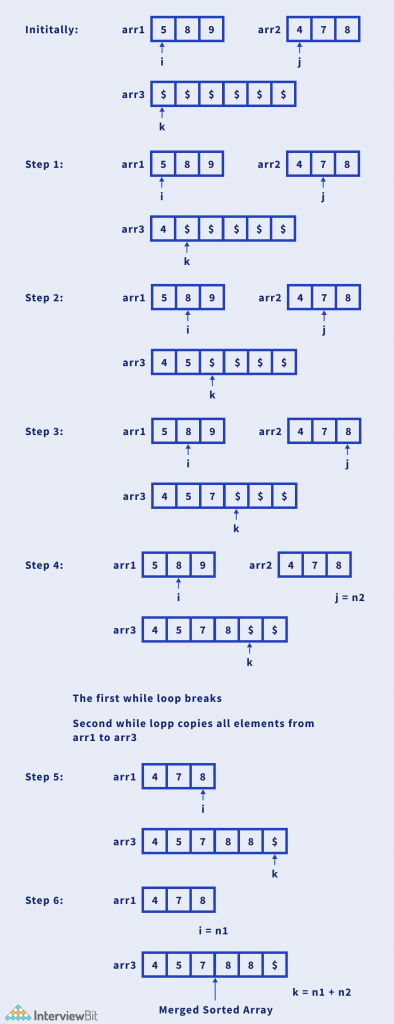
Algorithm
- Create an auxiliary array of size N + M.
- Put two pointers i and j and initialise them to 0.
- Pointer i points to the first array, whereas pointer j points to the second array.
- Traverse both the array simultaneously using the pointers, and pick the smallest elements among both the array and insert in into the auxiliary array.
- Increment the pointers.
- After traversal, return the merged array.
C++ Implementation
void mergeArrays(int arr1[], int arr2[], int n1,
int n2, int arr3[]) {
int i = 0, j = 0, k = 0;
while (i < n1 && j < n2) {
if (arr1[i] < arr2[j])
arr3[k++] = arr1[i++];
else
arr3[k++] = arr2[j++];
}
while (i < n1)
arr3[k++] = arr1[i++];
while (j < n2)
arr3[k++] = arr2[j++];
}Java Implementation
public static void mergeArrays(int[] arr1, int[] arr2, int n1,
int n2, int[] arr3) {
int i = 0, j = 0, k = 0;
while (i < n1 && j < n2) {
if (arr1[i] < arr2[j])
arr3[k++] = arr1[i++];
else
arr3[k++] = arr2[j++];
}
while (i < n1)
arr3[k++] = arr1[i++];
while (j < n2)
arr3[k++] = arr2[j++];
}Python Implementation
def mergeArrays(arr1, arr2, n1, n2):
arr3 = [None] * (n1 + n2)
i = 0
j = 0
k = 0
while i < n1 and j < n2:
if arr1[i] < arr2[j]:
arr3[k] = arr1[i]
k = k + 1
i = i + 1
else:
arr3[k] = arr2[j]
k = k + 1
j = j + 1
while i < n1:
arr3[k] = arr1[i]
k = k + 1
i = i + 1
while j < n2:
arr3[k] = arr2[j]
k = k + 1
j = j + 1Time Complexity:O(N + M), where N and M is the size of array A[] and B[]
Space Complexity:O(N + M), as the auxiliary array is used
FAQs
How is the space complexity O(1) for the two-pointers approach?
Since, we are in placing merging all the elements into the first array, without creating any other auxiliary space, the space complexity is O(1)
How is the two pointer approach different from the merge sort approach?
The merge sort approach considers an auxiliary array to sort and keeps two-pointer and the beginning of the array and merges accordingly.
Whereas, the two-pointer approach, starts iterating from backward and keeps merging the elements in place.




