Problem Statement
The Post Correspondence Problem is a popular undecidable decision problem, introduced by Emil Post in 1946. Being a problem, simpler than the Halting Problem, it is often used in proofs of undecidability.
The problem is stated formally as follows,
Given 2 lists of words, find if there exists a sequence such that the concatenation of the words in this order, gives the same word for both lists.
Confused about your next job?
For example,
Consider the lists,
a = [b, a, aba, bb]
b = [ba, ba, ab, b]
For these 2 lists, the sequence [1, 2, 1, 3, 3, 4] will give the solution for the Post Correspondence Problem. The String that will be formed in both cases will be “bababaababb” by following the above sequence.
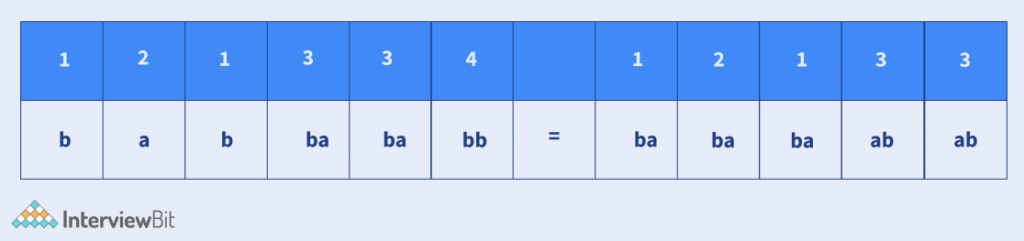
Representation of the Problem
Considering the 1st list to act as the numerator, and the 2nd list to act as the denominator for the problem, the problem can be represented in 2 forms:
Domino Form
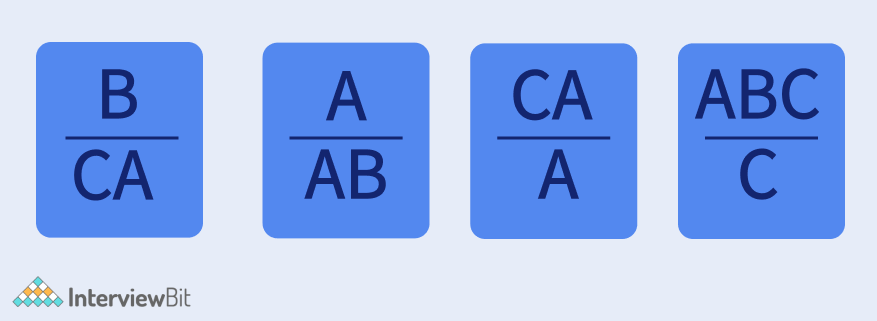
Table Form

Proof of Undecidability
Undecidability of a problem means that there is no specific algorithm, which can accurately determine, whether the given problem has a solution or not.
A well-known problem that is undecidable is the Turing Problem. So, if we can remodel/reduce the Turing Problem, into the Postman Correspondence Problem, we can prove its undecidability as well.
A brief sketch of the proof is as follows,
Consider an instance of the Postman Correspondence Problem, which can, on an arbitrary input, simulate the computation of an arbitrary Turing Machine. We note that a match will occur, if and only if the Turing Machine would accept the input. The problem of deciding whether a Turing Machine will accept the given input or not is a well-known undecidable problem. Since the Postman Correspondence Problem reduces into this particular problem, we can say the Postman Correspondence Problem is undecidable as well, which completes our proof.
FAQs
Ans: The Membership, Finiteness, and Emptiness of a Turing Machine are all well-known undecidable problems related to a Turing Machine.
Q.2: What is the Halting Problem?
Ans: The Halting Problem is the problem of determining from the given description of an arbitrary computer program and an input, whether will the program will terminate or will continue running indefinitely into the future,




