- Problem Statement
- Simple Approach
- Efficient Approach: Sieve of Eratosthenes
- Dry run of the above approach
- C++ Implementation Efficient Approach
- Java Implementation of Efficient Approach
- Python Implementation of Efficient Approach
- Analysis of Time Complexity
- Conclusion
- Practice Questions
- Frequently Asked Questions
Problem Statement
Given a number n, print all primes smaller than or equal to n. It is also given that n is a small number.
A prime number is a number that is divisible by only two numbers – themselves and 1
Example:
Confused about your next job?
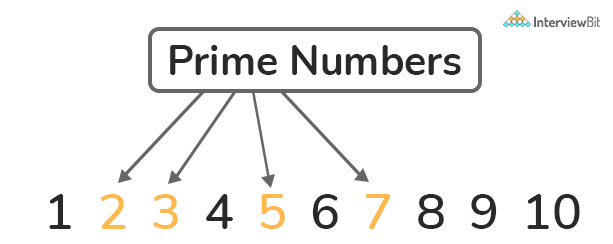
Input: n =10
Output: 2 3 5 7
Explanation: Only 4 prime numbers are there which are less than or equal to 10.
Input: n = 20
Output: 2 3 5 7 11 13 17 19
Explanation: All above numbers are prime which are less than or equal to 20.
Simple Approach
Iterate from 2 to N, and check for prime. If it is a prime number, print the number. Below is the implementation of the above approach
C++ Implementation
int checkPrime(int n) {
if (n <= 1)
return 0;
for (int i = 2; i < n; i++)
if (n % i == 0)
return 0;
return 1;
}
// Function to print all the prime numbers from
// range 2 to n
void printPrime(int n) {
for (int i = 2; i <= n; i++) {
if (checkPrime(i))
cout << i << " ";
}
}Java Implementation
class Interviewbit {
static int isPrime(int n) {
for (int i = 2; i < n; i++)
if (n % i == 0)
return 0;
return 1;
}
static void printPrime(int n) {
for (int i = 2; i <= n; i++) {
if (isPrime(i))
System.out.print(i + " ");
}
}
}Python Implementation
def isPrime(n):
# Corner case
if n <= 1 :
return False
# check from 2 to n-1
for i in range(2, n):
if n % i == 0:
return False
return True
# Function to print primes
def printPrime(n):
for i in range(2, n + 1):
if isPrime(i):
print(i, end = " ")Time complexity: O(N*N), Where N is the number.
Space complexity: O(1)
Efficient Approach: Sieve of Eratosthenes
The sieve of Eratosthenes is one of the most efficient ways to find all primes smaller than n when n is smaller than 10 million or so. Following is the algorithm to find all the prime numbers less than or equal to a given integer n by the Eratosthenes method:
When the algorithm terminates, all the numbers in the list that are not marked are prime.
- Firstly write all the numbers from 2,3,4…. n
- Now take the first prime number and mark all its multiples as visited.
- Now when you move forward take another number which is unvisited yet and then follow the same step-2 with that number.
- All numbers in the list left unmarked when the algorithm ends are referred to as prime numbers.
Dry run of the above approach
Step 1: The numbers between 1 and 100 are listed in the table below.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Step 2: The next step is to write in bold all the multiples of 2, except 2 itself.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Step 3: Now bold all multiples of 3, 5, and 7 and only leave these numbers.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Step 4: Since the multiples of 11, 13, 17, and 19 are not present on the list, 1 is finally shaded because it is not prime.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Step 5: The unshaded numbers are prime. They include:
2, 3, 5,7, 11, 13,17,19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
C++ Implementation Efficient Approach
void SieveOfEratosthenes(int n)
{
bool prime[n + 1];
memset(prime, true, sizeof(prime));
for (int p = 2; p * p <= n; p++)
{
if (prime[p] == true)
{
for (int i = p * p; i <= n; i += p)
prime[i] = false;
}
}
for (int p = 2; p <= n; p++)
if (prime[p])
cout << p << " ";
}Java Implementation of Efficient Approach
class SieveOfEratosthenes {
void sieveOfEratosthenes(int n)
{
boolean prime[] = new boolean[n + 1];
for (int i = 0; i <= n; i++)
prime[i] = true;
for (int p = 2; p * p <= n; p++){
if (prime[p] == true)
{
for (int i = p * p; i <= n; i += p)
prime[i] = false;
}
}
for (int i = 2; i <= n; i++)
{
if (prime[i] == true)
System.out.print(i + " ");
}
}
}Python Implementation of Efficient Approach
def SieveOfEratosthenes(n):
prime = [True for i in range(n+1)]
p = 2
while (p * p <= n):
if (prime[p] == True):
# Update all multiples of p
for i in range(p * p, n+1, p):
prime[i] = False
p += 1
# Print all prime numbers
for p in range(2, n+1):
if prime[p]:
print p,Time complexity of Sieve of Eratosthenes:
Space complexity: O(1)
Analysis of Time Complexity
- PREREQUISITE: Time complexity of the Harmonic Series is O(logN), when N is tending to infinity.
- If we analyze our sieve for larger numbers then we can see .
- The inner loop at each iteration can be expressed by:
- i=2, the inner loop will be executed → upper bound is (n/2) times
- i=3, the inner loop will be executed → upper bound is (n/3) times
- i=5, the inner loop will be executed → upper bound is (n/5) times
- …
- i=n(if prime number), the inner loop will be executed → upper bound is 1 times.
- The above series time complexity is less than harmonic series:
- n/2 + n/4 + ..+ 1 → n (1/2 + 1/3 + 1/4 + … 1/n),
- Hence, the run loop times should be
- n (1/2 + 1/3 + 1/5 + 1/7 + 1/ 11 + 1/13 + …).= logn That is why, in some article,
- The time complexity is defined in O(nloglogn).
Conclusion
The outer loop is a general for-loop from 1 to N, the time complexity is O(N). The total time complexity is O(NloglogN).
Practice Questions
Frequently Asked Questions
Q: How fast is Sieve of Eratosthenes?
A: It is very fast as it can store prime numbers up to the 1e7 range easily.
Q: How do you improve the sieve of Eratosthenes?
A: We can further improve the sieve to O(n) by writing it to an iterative sieve.
Q: How does the Sieve of Eratosthenes work?
A: It works on the principle of cancellation of prime factors.




