Problem Statement
Given a matrix A of size N X M. The task is to print the matrix in spiral order.
Examples:
Input: A[] = [[1, 2, 3, 4],
Confused about your next job?
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]
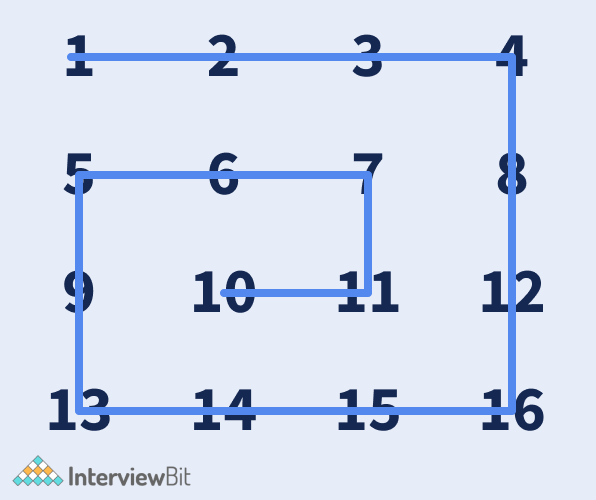
Output: [1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11 10]
Explanation: Shown in image
Approach 1: Iterative
The idea is to traverse the given matrix in the following manner:
- Traverse left to right.
- Traverse top to bottom.
- Traverse right to left
- Traverse bottom to top
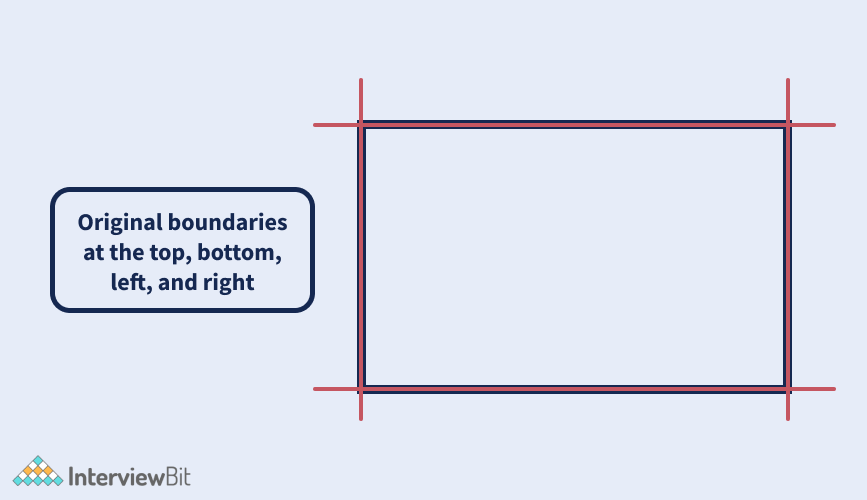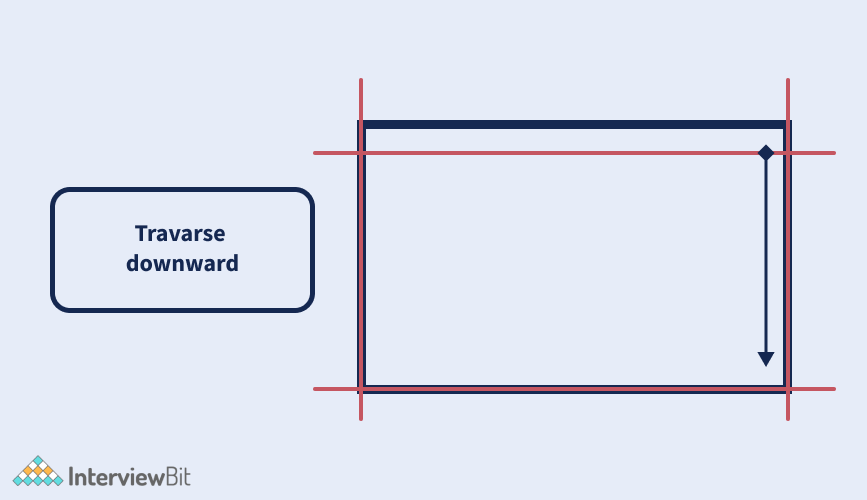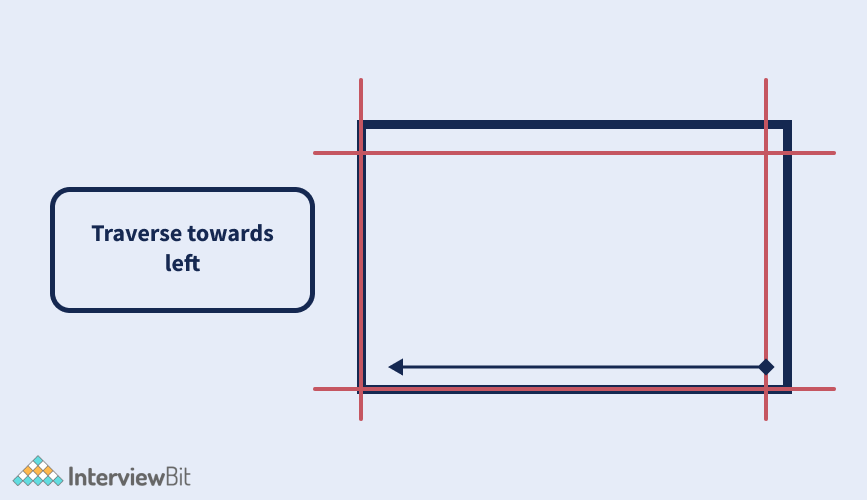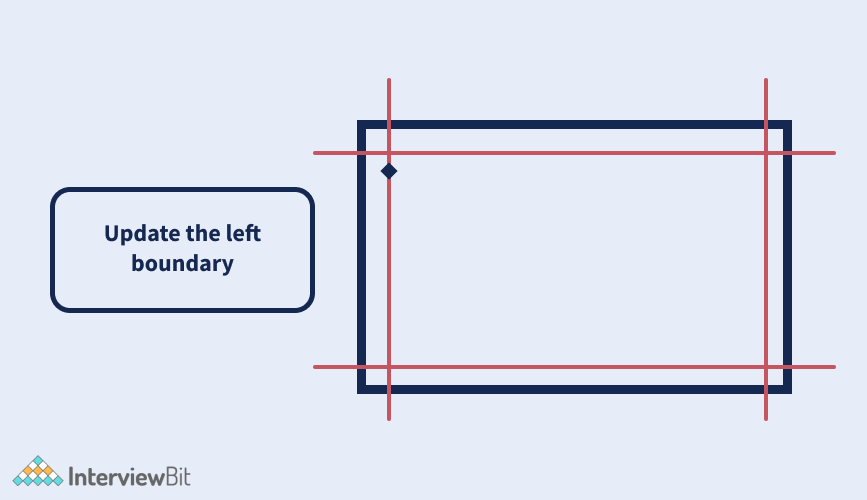
Continue these steps till all the elements have been visited.
Implementation of the Approach:
C++ Code
void spiralPrint(int m, int n, int a[R][C]) {
int i, k = 0, l = 0;
while (k < m && l < n) {
for (i = l; i < n; ++i) {
cout << a[k][i] << " ";
}
k++;
for (i = k; i < m; ++i) {
cout << a[i][n - 1] << " ";
}
n--;
if (k < m) {
for (i = n - 1; i >= l; --i) {
cout << a[m - 1][i] << " ";
}
m--;
}
if (l < n) {
for (i = m - 1; i >= k; --i) {
cout << a[i][l] << " ";
}
l++;
}
}
}Java Code
static void spiralPrint(int m, int n, int a[][]) {
int i, k = 0, l = 0;
while (k < m && l < n) {
for (i = l; i < n; ++i) {
System.out.print(a[k][i] + " ");
}
k++;
for (i = k; i < m; ++i) {
System.out.print(a[i][n - 1] + " ");
}
n--;
if (k < m) {
for (i = n - 1; i >= l; --i) {
System.out.print(a[m - 1][i] + " ");
}
m--;
}
if (l < n) {
for (i = m - 1; i >= k; --i) {
System.out.print(a[i][l] + " ");
}
l++;
}
}
}Python Code
def spiralPrint(m, n, a):
k = 0
l = 0
while k < m and l < n:
for i in range(l, n):
print(a[k][i], end=" ")
k += 1
for i in range(k, m):
print(a[i][n - 1], end=" ")
n -= 1
if k < m:
for i in range(n - 1, (l - 1), -1):
print(a[m - 1][i], end=" ")
m -= 1
if l < n:
for i in range(m - 1, k - 1, -1):
print(a[i][l], end=" ")
l += 1- Time Complexity: O(N * M), where N * M is the total size of the matrix
- Space Complexity: O(1), as no extra space is used.
Approach 2: Recursive Solution
Similar to the last approach, we can try to solve this problem recursively. The idea of this approach is exactly similar to the iterative approach.
Algorithm:
- Consider four variables, i.e. starting_row, ending_row, starting_col, ending_col.
- Create a recursive function for printing the spiral matrix.
- Base cases would be: If the starting index of row/col is less than the size of row/col, then, terminate the function, else continue printing the boundary elements.
- Run a loop from left to right and print the element.
- Similarly, run a loop from top to bottom and right to left, and bottom to top.
Implementation of the Approach:
C++ Code
void print(int arr[R][C], int i, int j, int m, int n) {
if (i >= m or j >= n)
return;
for (int p = j; p < n; p++)
cout << arr[i][p] << " ";
for (int p = i + 1; p < m; p++)
cout << arr[p][n - 1] << " ";
if ((m - 1) != i)
for (int p = n - 2; p >= j; p--)
cout << arr[m - 1][p] << " ";
if ((n - 1) != j)
for (int p = m - 2; p > i; p--)
cout << arr[p][j] << " ";
print(arr, i + 1, j + 1, m - 1, n - 1);
}Java Code
static void print(int arr[][], int i, int j, int m,
int n) {
if (i >= m || j >= n) {
return;
}
for (int p = i; p < n; p++) {
System.out.print(arr[i][p] + " ");
}
for (int p = i + 1; p < m; p++) {
System.out.print(arr[p][n - 1] + " ");
}
if ((m - 1) != i) {
for (int p = n - 2; p >= j; p--) {
System.out.print(arr[m - 1][p] + " ");
}
}
}Python Code
def printdata(arr, i, j, m, n):
if i >= m or j >= n:
return
for p in range(i, n):
print(arr[i][p], end=" ")
for p in range(i + 1, m):
print(arr[p][n - 1], end=" ")
if (m - 1) != i:
for p in range(n - 2, j - 1, -1):
print(arr[m - 1][p], end=" ")
if (n - 1) != j:
for p in range(m - 2, i, -1):
print(arr[p][j], end=" ")
printdata(arr, i + 1, j + 1, m - 1, n - 1)- Time Complexity: O(N * M), where N * M is the total size of the matrix
- Space Complexity: O(1), as no extra space is used.
Practice Questions:
FAQ
Q.1: What is the time and space complexity of the recursive approach?
Ans: The time and space complexity of the recursive approach is O(N * M) and O(1).
Q.2: How to traverse the matrix in an anti-clockwise direction?
Ans: The idea is the same. Just traverse the matrix from top to down, left to right, bottom to top and right to left.