26K
0
5 minute read

Stack Using 2 Queues

November 19, 2021
Stack Using 2 Queues
Table Of Contents
show

Problem Statement

Implement a class Stack, using 2 Queues, which can perform the following operations:

  • Push(): Push a value into the stack.
  • Pop(): Pop last inserted element from the stack.
  • Top(): Display the top element of the stack.
  • getSize(): Return the current size of the stack.

Sample Test Cases:

Input 1:
push(1)
push(2)
push(3)
top()
pop()
top()
pop()
top()
pop()

Confused about your next job?

In 4 simple steps you can find your personalised career roadmap in Software development for FREE



Expand in New Tab 

Output 1:
3
2
1

Explanation 1:

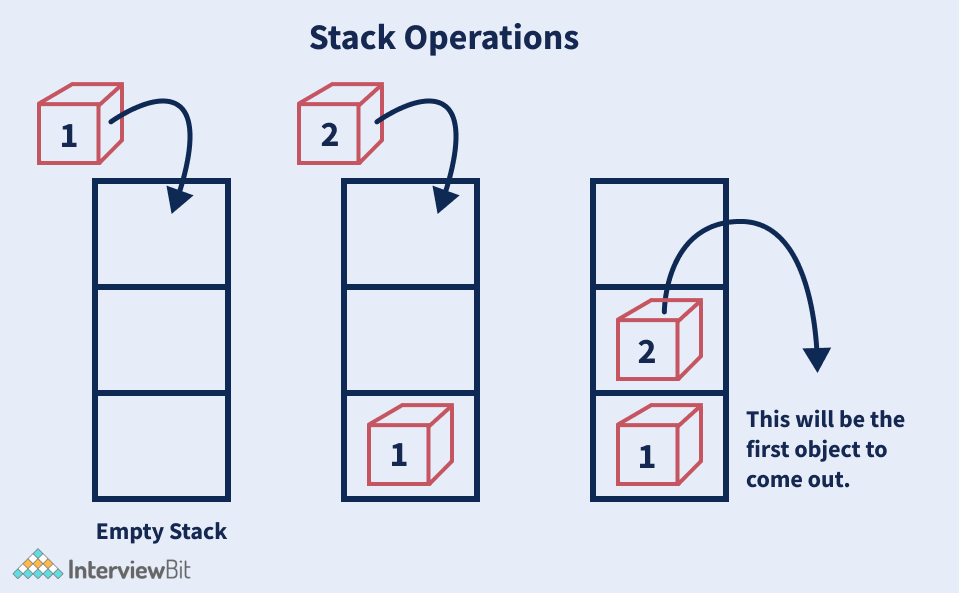
Stack follows a last in first out rule, so the elements which are inserted first are popped out last from the stack.

Stack Operations

Approach 1 (Push Operation costly)

Using 2 queues, we can make a stack, which can perform push operations in O(n) and all other functionalities in O(1) time. Let the queues be called firstQ and secondQ. We will ensure that the pop operation will only pop from the firstQ. secondQ is used to put every new element to the front of firstQ.

The implementation of the functions are described as follows:

  • push(val): 
    • Push val to secondQ.
    • Using a while loop, pop all the contents from firstQ and push them into secondQ in order.
    • Swap the 2 Queues.
  • pop(): 
    • Pop from the firstQ and reduce its size by 1.
  • top():
    • Return the top element from firstQ if it is not empty.
  • getSize():
    • Return the currentSize of the queue.

Code / Implementation:

C++ Code

class Stack {
  public:
    queue < int > firstQ, secondQ;
  int currentSize;
  Stack() {
    currentSize = 0;
  }
  int top() {
    return firstQ.empty() ? -1 : firstQ.front();
  }
  int getSize() {
    return currentSize;
  }
  void push(int val) {
    secondQ.push(val);
    currentSize += 1;
    while (!firstQ.empty()) {
      int x = firstQ.front();
      secondQ.push(x);
      firstQ.pop();
    }
    swap(firstQ, secondQ);
  }
  void pop() {
    if (!firstQ.empty()) {
      firstQ.pop();
      currentSize -= 1;
    }
    return;
  }
};

Java Code

public static class Stack {
  static Queue < Integer > firstQ = new LinkedList < Integer > ();
  static Queue < Integer > secondQ = new LinkedList < Integer > ();
  static int currentSize = 0;
  Stack() {
    currentSize = 0;
  }
  static int top() {
    return firstQ.isEmpty() ? -1 : firstQ.peek();
  }
  static int getSize() {
    return currentSize;
  }
  static void push(int val) {
    secondQ.add(val);
    currentSize += 1;
    while (!firstQ.isEmpty()) {
      int x = firstQ.peek();
      secondQ.add(x);
      firstQ.remove();
    }
    Queue < Integer > tempQ = firstQ;
    firstQ = secondQ;
    secondQ = tempQ;
  }
  static void pop() {
    if (!firstQ.isEmpty()) {
      firstQ.remove();
      currentSize -= 1;
    }
    return;
  }
}

Python Code

from queue import Queue


class Stack:
    def __init__(self):
        self.firstQ = Queue()
        self.secondQ = Queue()
        self.currentSize = 0

    def top(self):
        if self.firstQ.empty():
            return -1
        return self.firstQ.queue[0]

    def getSize(self):
        return self.currentSize

    def push(self, val):
        self.secondQ.put(val)
        self.currentSize += 1
        while not self.firstQ.empty():
            self.secondQ.put(self.firstQ.queue[0])
            self.firstQ.get()

        self.tempQ = self.firstQ
        self.firstQ = self.secondQ
        self.secondQ = self.tempQ

    def pop(self):
        if not self.firstQ.empty():
            self.firstQ.get()
            self.currentSize -= 1

Complexity Analysis:

  • Time Complexity: O(n) for push(), O(1) for the rest.
  • Space Complexity: O(n) for push(), O(1) for the rest.

Approach 2(Pop Operation Costly)

We can also form a Stack with 2 Queues, where the pop() and the top() operation works in O(n) and the other functionalities work in O(1). Our target will be that for each push operation, the element is just pushed to firstQ. For our pop operation, if the secondQ is currently empty, all but the last element from the firstQ will be moved to the secondQ. The last element from the secondQ can then be returned.

The algorithm for each function is as follows:

  • push(val): 
    • Push val to the front of firstQ.
  • pop():
    • Other than the very last element in the firstQ, pop everything out of it and push into the secondQ. The last element in the firstQ is the result.
    • Swap firstQ and secondQ.
  • top():
    • Perform the same steps as described in the pop operation, but return the value of the last element remaining in firstQ before swapping, unless the queue is empty.
  • getSize(): 
    • Return the current Stack size.

Implementation:

C++ Code

class Stack {
  public:
    queue < int > firstQ, secondQ;
  int currentSize;
  Stack() {
    currentSize = 0;
  }
  int top() {
    if (firstQ.empty()) {
      return -1;
    }
    int topEle = -1;
    while (firstQ.size() > 0) {
      int x = firstQ.front();
      if (firstQ.size() == 1) {
        topEle = x;
      }
      secondQ.push(x);
      firstQ.pop();
    }
    swap(firstQ, secondQ);
    return topEle;
  }
  int getSize() {
    return currentSize;
  }
  void push(int val) {
    firstQ.push(val);
    currentSize += 1;
  }
  void pop() {
    if (!firstQ.empty()) {
      while (firstQ.size() != 1) {
        int x = firstQ.front();
        secondQ.push(x);
        firstQ.pop();
      }
      firstQ.pop();
      currentSize -= 1;
      swap(firstQ, secondQ);
    }
  }
};

Java Code

static class Stack {
  static Queue < Integer > firstQ = new LinkedList < > ();
  static Queue < Integer > secondQ = new LinkedList < > ();
  static int currentSize = 0;
  Stack() {
    currentSize = 0;
  }
  static int top() {
    if (firstQ.isEmpty()) {
      return -1;
    }
    int topEle = -1;
    while (firstQ.size() > 0) {
      int x = firstQ.peek();
      if (firstQ.size() == 1) {
        topEle = x;
      }
      secondQ.add(x);
      firstQ.remove();
    }
    Queue < Integer > tempQ = firstQ;
    firstQ = secondQ;
    secondQ = tempQ;
  return topEle;
  }
  static int getSize() {
    return currentSize;
  }
  static void push(int val) {
    firstQ.add(val);
    currentSize += 1;
  }
  static void pop() {
    if (!firstQ.isEmpty()) {
      while (firstQ.size() != 1) {
        int x = firstQ.peek();
        secondQ.add(x);
        firstQ.remove();
      }
      firstQ.remove();
      currentSize -= 1;
      Queue < Integer > tempQ = firstQ;
      firstQ = secondQ;
      secondQ = tempQ;
    }
  }
}

Python Code

from queue import Queue


class Stack:
    def __init__(self):
        self.firstQ = Queue()
        self.secondQ = Queue()
        self.currentSize = 0

    def top(self):
        if self.firstQ.empty():
            return -1
        while self.firstQ.qsize() != 1:
            x = self.firstQ.get()
            self.secondQ.put(x)
        topEle = self.firstQ.get()
  self.secondQ.put(topEle)
        self.tempQ = self.firstQ
        self.firstQ = self.secondQ
        self.secondQ = self.tempQ
        return topEle

    def getSize(self):
        return self.currentSize

    def push(self, val):
        self.firstQ.put(val)
        self.currentSize += 1

    def pop(self):
        if not self.firstQ.empty():
            while self.firstQ.qsize() != 1:
                x = self.firstQ.get()
                self.secondQ.put(x)
            last = self.firstQ.get()
            self.currentSize -= 1
            self.tempQ = self.firstQ
            self.firstQ = self.secondQ
            self.secondQ = self.tempQ
        else:
            return

Complexity Analysis:

  • Time Complexity: O(n) for top() and pop() operations, O(1) for the rest
  • Space Complexity: O(n) for top() and pop() operations, O(1) for the rest

FAQs

1. What is the minimum number of Queues required to implement a Stack?

A. A minimum of 2 queues is required to implement a Stack.

2. Other than queues, what data structures can be used to implement Stacks?

A. Other than queues, stacks can also be implemented using LinkedList and/or Arrays.

0
0
0
0
Share 0
Tweet 0
Pin it 0
Share 0
Share
Share
Share
Tweet
Previous Post
Construct Tree From Inorder and Preorder

Construct Tree from Inorder and Preorder

November 19, 2021
Next Post
Vertex Cover Problem

Vertex Cover Problem

November 19, 2021
Total
0
Share
0
0
0
0
0