Subarray With Given Sum

Problem Statement

Given an array of integers, the task is to find a non-empty subarray that adds to the given sum. If there exists more than one print, anyone.

Example:

Input: 11, 9, 8, 7,13, 5, 17
Sum = 25

Output: YES
Explanation: Subarray [7,13,5] sum up to 25 .

Input: 1,3,4,8,7,9
Sum = 13

Output: No
Explanation: No such subarray is present having sum 13.

Naive Approach

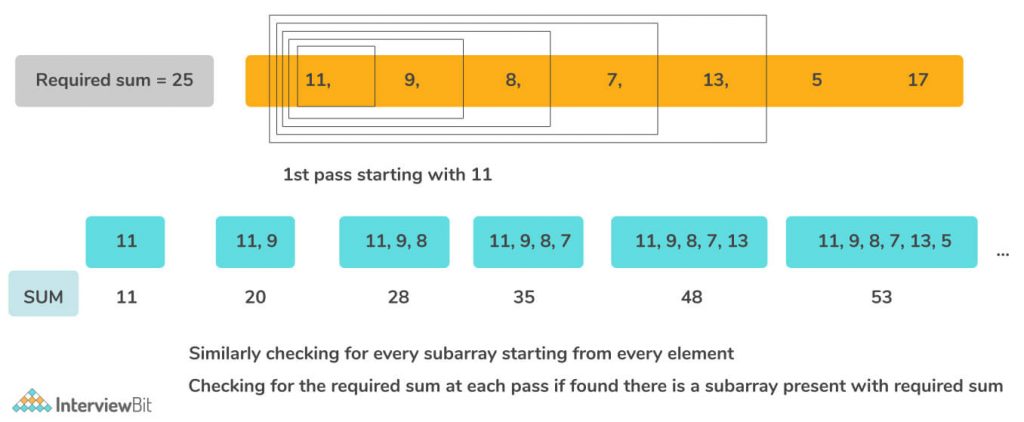
The naive approach is to check for every subarray for the given sum.

• Run a loop for i from [0…n-1] for the subarray starting from the i-th element.
• And run a nested loop to check for every length of subarray starting from position i.
• Every time check for the sum of the elements from i to j whether it’s equal to the required sum.

C++ Implementation

bool find_Subarray(int arr[], int N, int required) {
  int sum = 0;
  for (int i = 0; i < N; i++) {
    sum = arr[i];
    for (int j = i + 1; j < N + 1; j++) {
      if (sum == required) {
        // found subarray with given sum
        return true;
      } else if (sum > required) {
        break;
      }
      sum = sum + arr[j];
    }
  }
  return false;
}

Java Implementation

bool find_subarray(int arr[], int N, int required) {
  int sum;
  for (int i = 0; i < N; i++) {
    sum = arr[i];
    for (int j = i + 1; j <= N; j++) {
      if (sum == required) {
        // subarray found from i to j-1;
        return true;
      }
      if (sum > required || j == N)
        break;
      sum = sum + arr[j];
    }
  }
  return false;
}

Python Implementation

def find_subarray(arr, n, required):

    for i in range(n):
        sum = arr[i]
        j = i + 1
        while j <= n:
            if sum == required:
                return true
            if sum > required or j == n:
                break
            sum = sum + arr[j]
            j += 1
    return false

Time complexity: O(N^2), Where N is the size of the array.
Space complexity: O(1)

Efficient Approach: Sliding window

In a sliding window we take an empty window and move the upper bound of the window till our given constraint is satisfied and after that, if the constraints are violated we try to maintain the constraints by increasing or decreasing the size of the window.

The efficient approach is similar as we have constrained the sum and we take the window empty initially and if the sum of the window is greater than the required sum then it’s clear that adding any element more will increase the sum, so we remove the elements from the starting of the window till the sum of the window is less than the required sum and move forward in a similar manner.

• We have to take two variables one for the current sum and the other for the starting index of the window
• Check if the current sum is less than or equal to the required sum.
• If less then add the new element to the current sum.
• If equal, return true.
• If the current sum exceeds the required sum, subtract the arr[start] from the current sum and change start=start+1.
• If we return from the nested loop then we could not find any desired subarray so return false.

C++ Implementation of Efficient Approach

bool FindSubarray(int array[], int n, int required_sum) {
  int current_sum = array[0];
  int start = 0;
  for (int i = 1; i <= n; i++) {
    while (current_sum > required_sum && start < i - 1) {
      current_sum = current_sum - array[start];
      start++;
    }
    if (current_sum == required_sum) {
      return true;
    }
    if (i < n) {
      current_sum = current_sum + array[i];
    }
  }
  return false
}

Java Implementation of Efficient Approach

public static bool Find_Subarray(int array[], int n, int required) {
  int sum = array[0];
  int start = 0;
  for (int i = 1; i <= n; i++) {
    while (sum > required && start < i - 1) {
      sum = sum - array[start];
      start++;
    }
    if (sum == required) {
      return true;
    }
    if (i < n) {
      sum = sum + array[i];
    }
  }
  return false;
}

Python Implementation of Efficient Approach

def Find_Subarray(array, n, required):

    sum = array[0]
    start = 0
    i = 1
    while i <= n:

        while sum > required and start < i - 1:

            sum = sum - array[start]
            start += 1
        if sum == required:
            return true

        if i < n:
            sum = sum + array[i]
        i += 1

    return false

Practice Questions

Counting Subarrays
Maximum Product Subarray
Subarrays With Distinct Integers