Problem Statement
Given a Knapsack/Bag with W weight capacity and a list of N items with given vi value and wi weight. Put these items in the knapsack in order to maximise the value of all the placed items without exceeding the limit of the Knapsack.
0-1 Knapsack Problem
The problem remains the same but one cannot break the items you can either select it fully ( 1) or don’t select it (0 ).
Confused about your next job?
Example of 0-1 Knapsack :
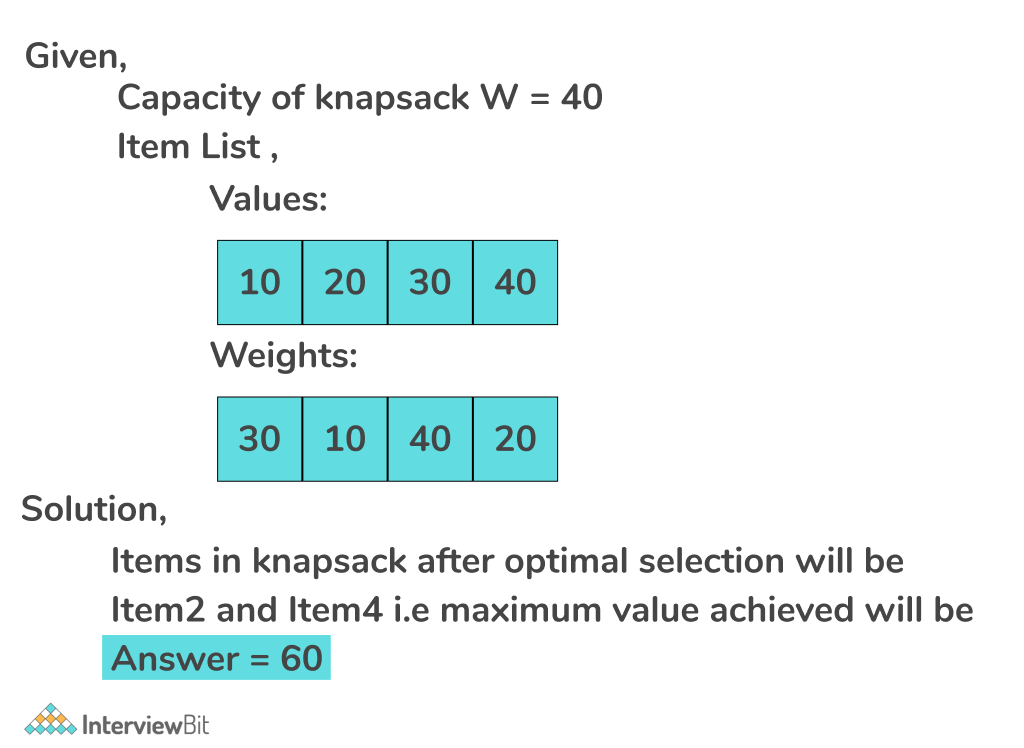
Method 1 (Using Bruteforce Recursion):
Our approach with recursion will be to try and create all the subsets of items with total weight less than that of the given capacity W. From the result we will return the subset with maximum value.
For every element we can,
- either select it or,
- ignore and move forward.
If we select an item then its value will be added to our current value and weight will be subtracted from the current available space.
Thus, if we take the maximum value out of both the calculated result for nth element i.e. result after selecting that element and after ignoring it, we can get to our desired answer.
Code for Above Implementation:
C++ Code
int knapsack01(int W,int N,vector<int> &v,vector<int> &w) {
/* Base case 0 items left or knapsack is full */
if(N == 0 || W == 0)
return 0;
/* if weight of current element is less than or equal to capacity we can
either include or exclude the item. */
if(w[N] <= W){
return max(v[N]+knapsack01(W-w[N],N-1,v,w),knapsack01(W,N-1,v,w));
}
/* if weight of current element is greater than the capacity we will
not include it thus returning just the ignoring part. */
return knapsack01(W,N-1,v,w);
}Java Code
// maximum Function for max of two integers
static int max(int a, int b) {
if(a>b) return a;
else return b;
}
static int knapSack(int W,int N,int v[],int w[]) {
/* Base case 0 items left or knapsack is full */
if(N == 0 || W == 0)
return 0;
/* if weight of current element is less than or equal to capacity we can
either include or exclude the item. */
if(w[N] <= W){
return max(v[N]+knapSack(W-w[N],N-1,v,w),knapSack(W,N-1,v,w));
}
/* if weight of current element is greater than the capacity we will
not include it thus returning just the ignoring part. */
return knapSack(W,N-1,v,w);
}
Python Code
def knapsack01(W,N,v,w):
# Base case 0 items left or knapsack is full
if N == 0 or W == 0:
return 0
# if weight of current element is less than or equal to capacity we can
# either include or exclude the item.
if w[N] <= W:
return max(v[N]+knapsack01(W-w[N],N-1,v,w),knapsack01(W,N-1,v,w))
# if weight of current element is greater than the capacity we will
# not include it thus returning just the ignoring part.
else:
return knapsack01(W,N-1,v,w)
- Time Complexity of the above approach is O(2n).
Method 2 (Using Dynamic Programming):
In the above approach, we can observe that we are calling recursion for the same sub-problems again and again thus resulting in overlapping subproblems thus we can make use of Dynamic programming to solve the 0-1 Knapsack problem.
For Example :

Approach 1: (Using memoization)
In this approach, we’ll store all the computed answers in a 2 dimensional Array with indices of items in rows and weights in columns and use it further for overlapping subproblems.
Code for Above Implementation:
C++ Code
int knapSackrecur(int W,int N,vector<int> &v,vector<int> &w,vector<vector<int>>& dp){
/* Base case 0 items left or knapsack is full */
if(N == 0 || W == 0)
return 0;
/* Checking if the result exists in DP */
if(dp[N][W]!=-1)
return dp[N][W];
/* if weight of current element is less than or equal to capacity we can
either include or exclude the item and store it to DP. */
if(w[N] <= W){
return dp[N][W] = max(v[N]+knapSackrecur(W-w[N],N-1,v,w,dp),knapSackrecur(W,N-1,v,w,dp));
}
/* if weight of current element is greater than the capacity we will
not include it thus returning just the ignoring part and storing it to DP. */
return dp[N][W] = knapSackrecur(W,N-1,v,w,dp);
}
int knapsack01(int W,int N,vector<int> &v,vector<int> &w) {
// Defining Dp and initializing with -1.
vector<vector<int>> dp(N+1,vector<int> (W+1,-1));
return knapSackrecur(W,N-1,v,w,dp);
}
Java Code
// maximum of two integers
static int max(int a, int b) {
if(a>b) return a;
else return b;
}
static int knapSack(int W,int N,int v[],int w[],int [][]dp) {
/* Base case 0 items left or knapsack is full */
if(N == 0 || W == 0)
return 0;
if(dp[N][W] == -1)
return dp[N][W];
/* if weight of current element is less than or equal to capacity we can
either include or exclude the item. */
if(w[N] <= W){
return dp[N][W] = max(v[N]+knapSack(W-w[N],N-1,v,w),knapSack(W,N-1,v,w));
}
/* if weight of current element is greater than the capacity we will
not include it thus returning just the ignoring part. */
return dp[N][W] = knapSack(W,N-1,v,w);
}
static int knapsack01(int W,int N,int v[],int w[]){
// Defining Dp and initializing with -1.
int DP[][] = new int [N+1][W+1];
for(int i=0;i<=N;i++){
for(int j=0;j<=W;j++){
DP[i][j] = -1;
}
}
return knapSack(W,N,v,w,DP);
}
Python Code
# Globally defining the DP and initialising as -1
dp = [[-1 for i in range(W+1)] for j in range(N+1)]
def knapSack(W,N,v,w):
# Base case 0 items left or knapsack is full
if N == 0 or W == 0:
return 0
# checking if the result is precalculated and returning it.
if dp[N][W] != -1:
return dp[N][W]
# if weight of current element is less than or equal to capacity we can
# either include or exclude the item.
if w[N] <= W:
return dp[N][W] = max(v[N]+knapSack(W-w[N],N-1,v,w),knapSack(W,N-1,v,w))
# if weight of current element is greater than the capacity we will
# not include it thus returning just the ignoring part.
else:
return dp[N][W] = knapSack(W,N-1,v,w)
- Time Complexity of the above approach is O(N*W).
- Space Complexity of the above approach is O(N*W).
Approach 2: (Using Iterative DP)
In this approach, we’ll define 2 dimensional DP of the index for items defined on rows whereas weights from 1 to W on columns and for every weight we can compute the answer for placing items till the nth item.
Similar to the recursive approach we can define two cases that are,
- Use this item or
- Ignore it.
Thus for every, Dp[i][j] we can calculate values for these two cases and store out the maximum of those two,
Therefore we can get our answer for {i,j} as ,
DP[i][j] = max(v[i] + DP[i-1][j-w[i]],DP[i-1][j])
Code for Above Implementation
C++ Code
int knapsack01(int W,int N,vector<int> &v,vector<int> &w) {
int DP[N+1][W+1]; // Defining DP
/* If there is no space left that is W reaches 0 then DP[i][0]
for every i will be 0.*/
for(int i=0;i<N+1;i++) DP[i][0] = 0;
/* If there are no items left that is N reaches 0 then DP[0][i]
for every i will be 0.*/
for(int i=0;i<W+1;i++) DP[0][i] = 0;
for(int i=1;i<N+1;i++){
for(int j=1;j<W+1;j++){
if(w[i-1] <= j){
/* Taking max of both the cases i.e to take that
item or to ignore it.*/
DP[i][j] = max(v[i-1]+DP[i-1][j-w[i-1]],DP[i-1][j]);
}
else{
/* If the weight of current element is greater
than the space left in the bag we'll ignore it.*/
DP[i][j] = DP[i-1][j];
}
}
}
/* returning answer for W space and N items */
return DP[N][W]; }Java Code
static int knapSack(int W,int N,int v[],int w[]) {
int DP[][] = new int[N+1][W+1]; // Defining DP
/* If there is no space left that is W reaches 0 then DP[i][0]
for every i will be 0.*/
for(int i=0;i<N+1;i++) DP[i][0] = 0;
/* If there are no items left that is N reaches 0 then DP[0][i]
for every i will be 0.*/
for(int i=0;i<W+1;i++) DP[0][i] = 0;
for(int i=1;i<N+1;i++){
for(int j=1;j<W+1;j++){
if(w[i-1] <= j){
/* Taking max of both the cases i.e to take that
item or to ignore it.*/
int a = v[i-1]+DP[i-1][j-w[i-1]];
int b = DP[i-1][j];
if(a>b) DP[i][j] = a;
else DP[i][j] = b;
}
else{
/* If the weight of current element is greater
than the space left in the bag we'll ignore it.*/
DP[i][j] = DP[i-1][j];
}
}
}
/* returning answer for W space and N items */
return DP[N][W];
}Python Code
def knapsack01(W,N,v,w) :
DP = [[0 for i in range(W+1)] for j in range(N+1)] # Defining DP
for i in range(1,N+1) :
for j in range(1,W+1) :
if w[i-1] <= j :
# Taking max of both the cases i.e to take that
# item or to ignore it.
DP[i][j] = max(v[i-1]+DP[i-1][j-w[i-1]],DP[i-1][j])
else :
# If the weight of current element is greater
# than the space left in the bag we'll ignore it.
DP[i][j] = DP[i-1][j]
# returning answer for W space and N items
return DP[N][W]
- Time Complexity of the above approach is O(N*W).
- Space Complexity of the above approach is O(N*W).
Approach 3: (Space-optimized solution)
In the above approach, we used a 2D array to store the computed results in our DP but we can observe one thing that to compute the result for the nth element we just need the results for the (n-1)th element thus we do not need the rest of the result.
Therefore, if we just get the results for the (n-1)th element we can reach the nth result.
Thus we can reduce the size of our DP to 1D by just storing the results on different weights till the previous element.
Code For the above Implementation :
C++ Code
int knapsack01(int W,int N,vector<int> &v,vector<int> &w) {
int DP[W+1]; // Defining DP
/* For N = 0 defining DP[i] = 0.*/
for(int i=0;i<W+1;i++) DP[i] = 0;
for(int i=1;i<N+1;i++){
for(int j=W;j>=w[i-1];j--){
/* Taking max of both the cases i.e to take that
item or to ignore it.*/
DP[j] = max(v[i-1]+DP[j-w[i-1]],DP[j]);
}
}
/* returning answer for W space and N items */
return DP[W];
}Java Code
static int knapSack(int W,int N,int v[],int w[]) {
int DP[] = new int[W+1]; // Defining DP
/* For N = 0 defining DP[i] = 0.*/
for(int i=0;i<W+1;i++) DP[i] = 0;
for(int i=1;i<N+1;i++){
for(int j=W;j>=w[i-1];j--){
/* Taking max of both the cases i.e to take that
item or to ignore it.*/
int a = v[i-1]+DP[j-w[i-1]];
int b = DP[j];
if(a>b) DP[j] = a;
else DP[j] = b;
}
}
/* returning answer for W space and N items */
return DP[W];
}Python Code
def knapsack01(W,N,v,w) :
DP = [0 for i in range(W+1)] # Defining DP
for i in range(1,N+1) :
for j in range(W,w[i-1]-1,-1) :
# Taking max of both the cases i.e to take that
# item or to ignore it.
DP[j] = max(v[i-1]+DP[j-w[i-1]],DP[j])
# returning answer for W space and N items
return DP[W]
- Time Complexity of the above approach is O(N*W).
- Space Complexity of the above approach is O(W).
Practice Question
FAQs
Q.1: Can we solve the 0/1 Knapsack Problem using Backtracking?
Ans: Yes, the recursive DP approach itself is the backtracking approach for 0/1 knapsack.
Q.2: What is the Time Complexity of 0/1 Knapsack Problem?
Ans: The time complexity for the 0/1 Knapsack problem solved using DP is O(N*W) where N denotes the number of items available and W denotes the capacity of the knapsack.
Q.3: Can we solve the 0/1 Knapsack Problem using Greedy Algorithm?
Ans: No, the 0/1 Knapsack Problem cannot be solved using a greedy approach.




