Container With Most Water

Problem Statement

Given n non-negative integers a1, a2, …, an, where each represents a point at coordinate (i, ai). ‘n’ vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0).
Find two lines, which together with the x-axis form a container, such that the container contains the most water.

Your program should return an integer that corresponds to the maximum area of water that can be contained ( Yes, we know maximum area instead of maximum volume sounds weird.
But this is a 2D plane we are working with for simplicity ).

Note: You may not slant the container.

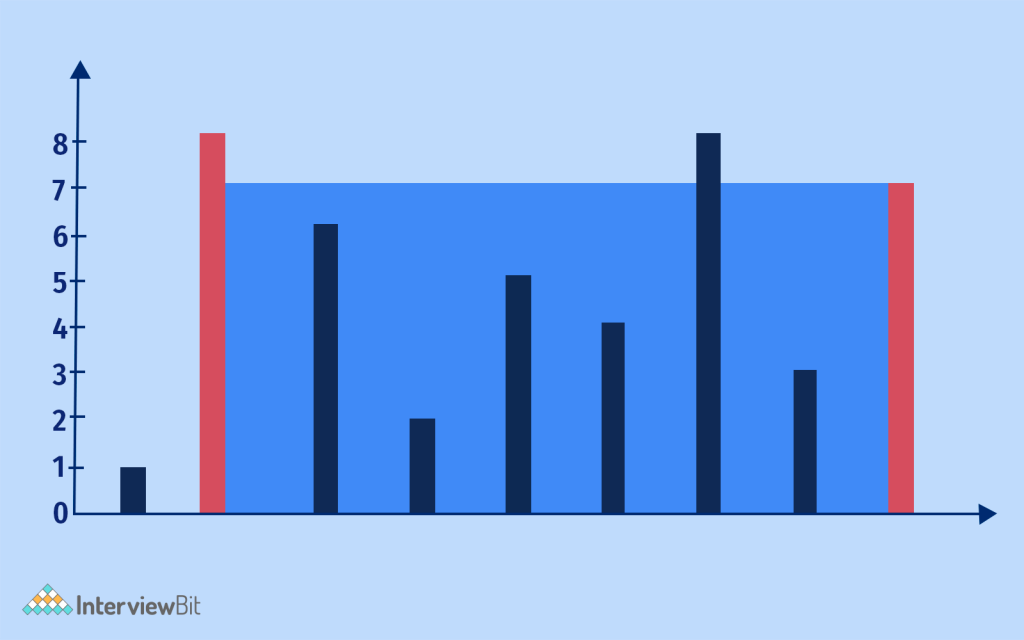
• Examples:Input:  height[] = {1,8,6,2,5,4,8,3,7} 
• Output: 49
• Explanation: The maximum area is the area denoted by the blue section. The total area is 49 units.

• Input:  height[] = {1, 1} 
• Output: 1

Approach 1: Brute Force

The most basic approach to solve this problem is to simplify all possible areas for every pair of line segments and maximize it.

Algorithm

• Initialise maxarea = 0.
• Run a nested loop i = 0 till i = N and j = i + 1 till N.
  • The area would be the min(height[i], height[j]) * (j – i)
  • Maximize the area for every iteration.
• Return maxarea.

C++ Code Implementation

int maxArea(vector<int> height) {
    int maxarea = 0;
    for (int i = 0; i < height.size(); i++)
      for (int j = i + 1; j < height.size(); j++)
        maxarea = max(maxarea, min(height[i], height[j]) * (j - i));
    return maxarea;
 }

Java Code Implementation

public class Solution {
  public int maxArea(int[] height) {
    int maxarea = 0;
    for (int i = 0; i < height.length; i++)
      for (int j = i + 1; j < height.length; j++)
        maxarea = Math.max(maxarea, Math.min(height[i], height[j]) * (j - i));
    return maxarea;
  }
}

Python Code Implementation

def maxArea(heights):
    maxarea = 0
    for i in range(len(heights)):
        for j in range(i + 1, len(heights)):
            maxarea = max(min(heights[i], heights[j]) * (j - i)
    return maxarea

• Time Complexity: O(N^2), where N is the size of the array
• Space Complexity: O(1) since no extra space is used.

Approach 2: Two Pointers

The most basic observation is that the area formed between the lines will always be limited by the height of the minimum. So, the larger the distance, the greater the area.
Check the below illustration to solve the problem:

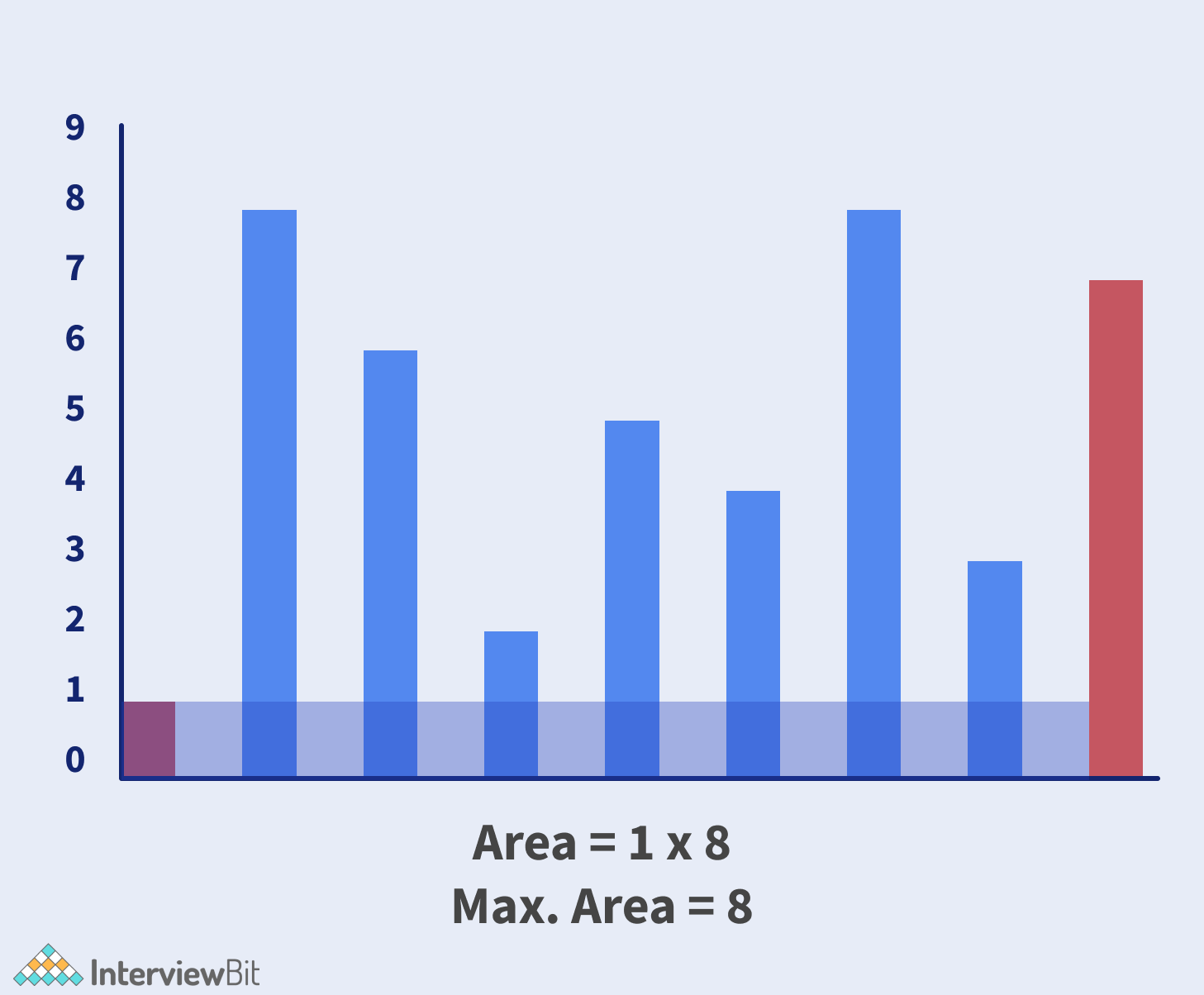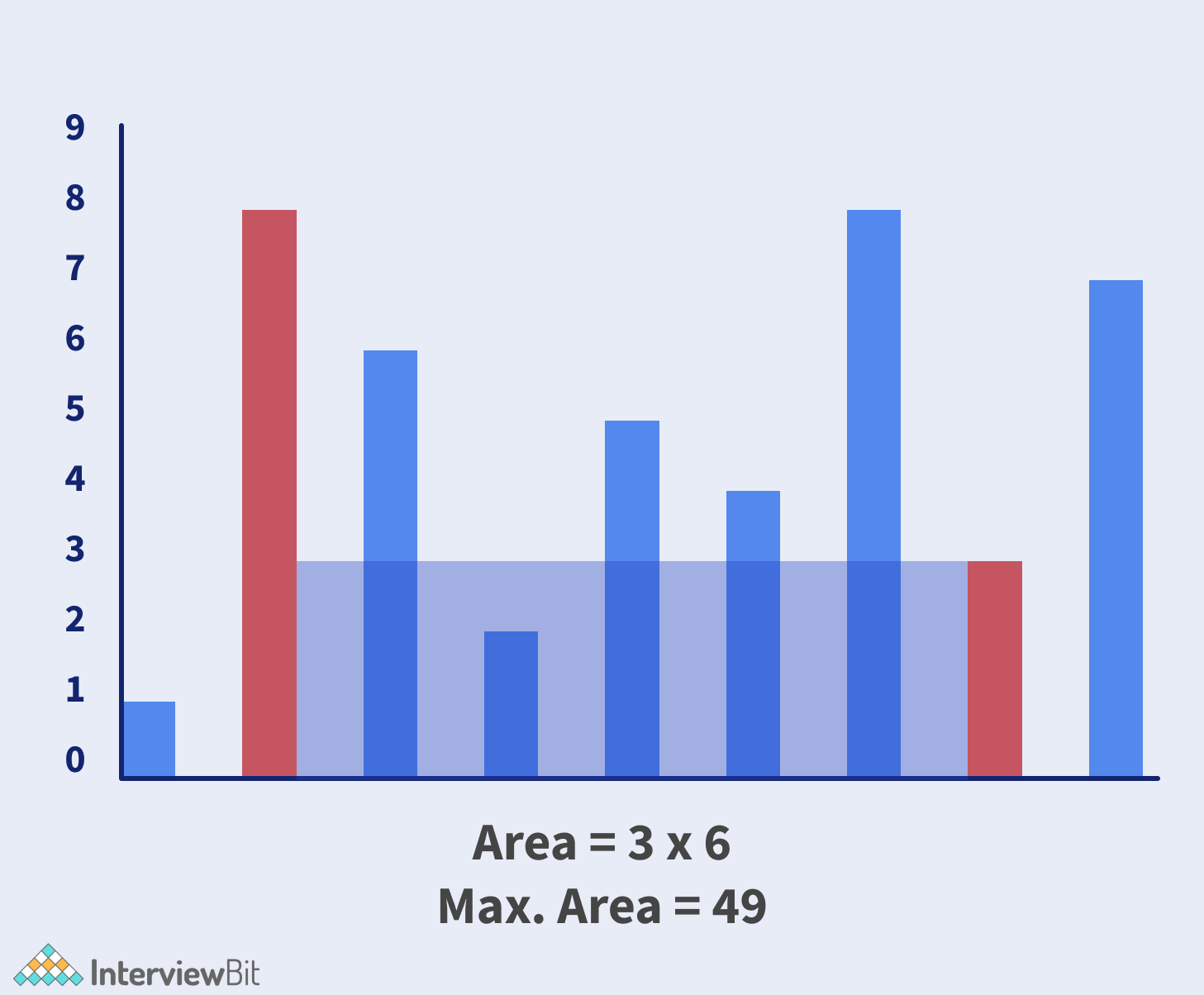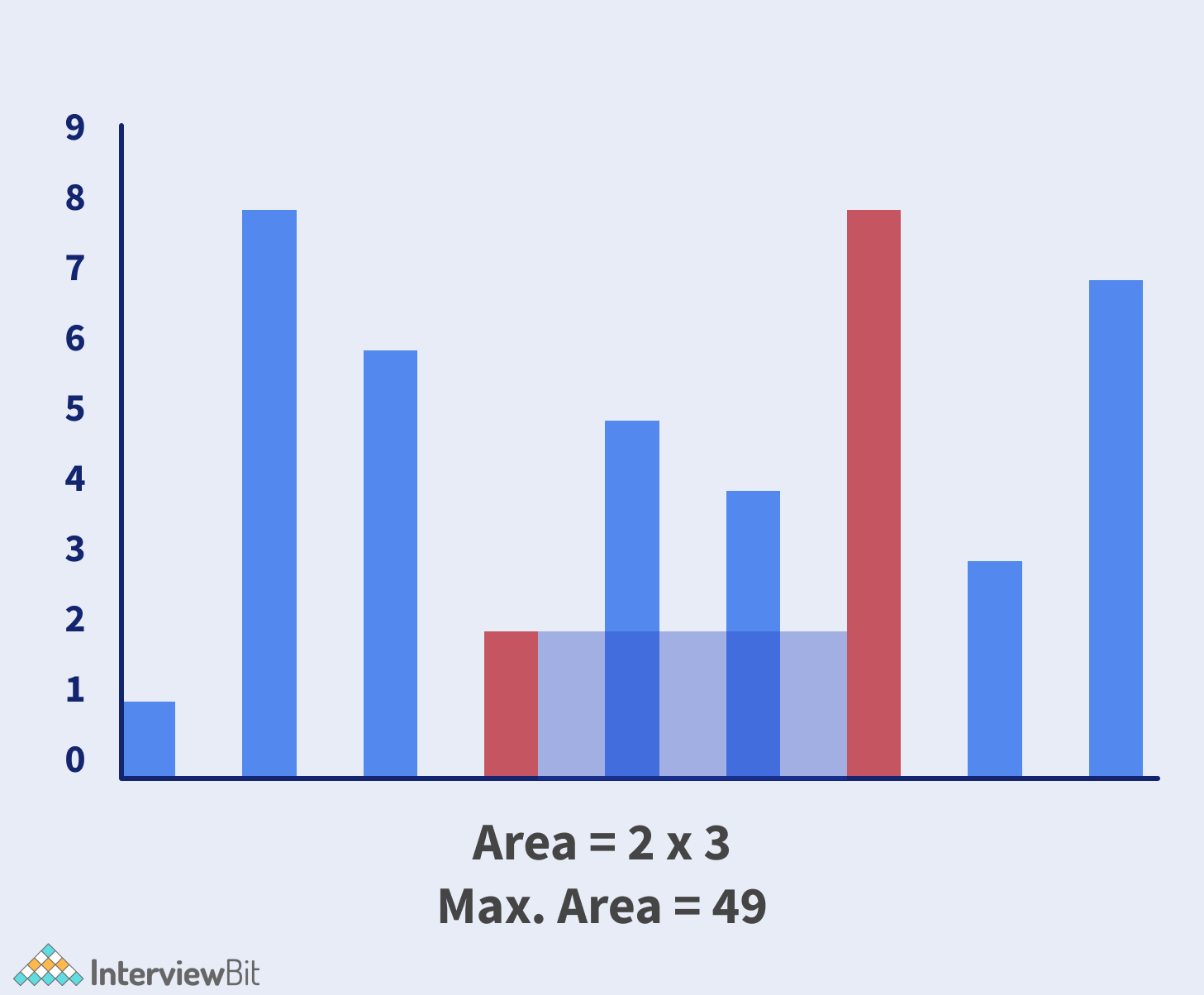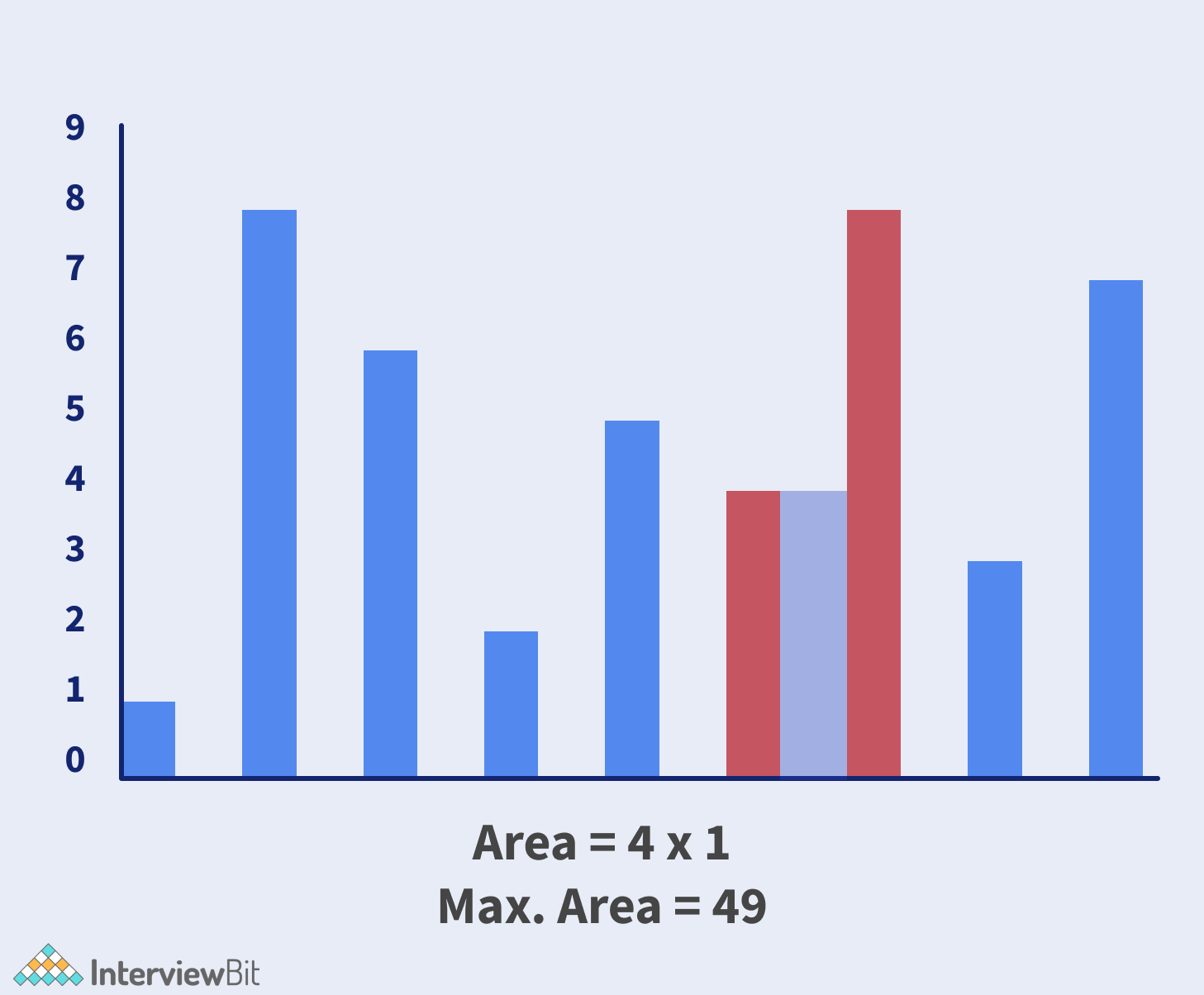
Algorithm:

• Take two pointers, one at i = 0 and another pointer j = N – 1.
• Consider a variable maxarea = 0, for calculating maxarea till index i.
• At every step, calculate the maxarea between them the two lines pointed i.e. height[i] and height[j] and update maxarea.
• Keep incrementing the pointer pointed at a smaller height towards each other.

C++ Code Implementation

int maxArea(vector<int> height) {
    int maxarea = 0, l = 0, r = height.size() - 1;
    while (l < r) {
      maxarea = max(maxarea, min(height[l], height[r]) * (r - l));
      if (height[l] < height[r])
        l++;
      else
        r--;
    }
    return maxarea;
  }

Java Code Implementation

public class Solution {
  public int maxArea(int[] height) {
    int maxarea = 0, l = 0, r = height.length - 1;
    while (l < r) {
      maxarea = Math.max(maxarea, Math.min(height[l], height[r]) * (r - l));
      if (height[l] < height[r])
        l++;
      else
        r--;
    }
    return maxarea;
  }
}

Python Code Implementation

def maxArea(height):
    L, R, width, res = 0, len(height) - 1, len(height) - 1, 0
    for w in range(width, 0, -1):
        if height[L] < height[R]:
            res, L = max(res, height[L] * w), L + 1
        else:
            res, R = max(res, height[R] * w), R - 1
    return res

• Time Complexity: O(N),  where N is the size of the array
• Space Complexity: O(1) since no extra space is used.

Practice Question

• Container With Most Water

FAQs

Q.1: How is the area between the two points found?

Ans: Since the width of each consecutive block is considered to be 1, the length is simply the distance between the two points and the height is the minimum between the two heights.

Q.2: What is the most efficient approach to solving this problem?

Ans: The two-pointer method is the most efficient way to solve this problem. The time complexity is O(N) and the space complexity is O(1).