Count The Triplets Problem

Problem Statement

Given an array A[] consisting of N integers. The task is to count the number of triples (A[i], A[j], A[k]), where i, j, and k denote the respective indices, such that one of the integers can be written as the summation of the other two integers.

Examples:

Input:  A[] = {1, 2, 3, 4, 5}
Output: 4
Explanation:
The valid triplets are –

• (1, 2, 3) : 1 + 2 = 3
• (2, 3, 5) : 2 + 3 = 5
• (1, 3, 4) : 1 + 3 = 4
• (1, 4, 5) : 1 + 4 = 5

Input: A[] = {2, 3, 6,9}
Output: 1

Basic Approach

The most basic approach is to run three nested loops from 1 till N and check if the summation of any two integers equals the third integer.

C++ Implementation

Java Implementation

Python Implementation

Time Complexity: O(N^3) where N is the number of nodes of the binary tree.Space Complexity: O(1)

Efficient Approach (Using Hashing)

The approach is to calculate all possible combinations such that the summation of any two integers is equal to the third integers. If we observe carefully, there can only be 4 possible cases, which satisfy the above condition.

• (0, 0, 0) : As 0 + 0 = 0, it is a valid triplet. Therefore, the total possible ways = freq[0]C3, as among all possible frequencies of 0, we just need to consider triplets.
• (0, x, x) : As 0 + x = x, it is a valid triplet. Therefore, the total possible ways = freq[x]C2 * freq[0]C1, as among all possible frequencies of 0 and x, we just need to consider the triplet containing one 0 and two x.
• (x, x, 2x) : As x + x = 2x, it is a valid triplet. Therefore, the total possible ways = freq[x]C2 * freq[2x]C1, as among all possible frequencies of x and 2x, we just need to consider the triplet containing one 2x and one x.
• (x, y, x + y) : The total possible ways = freq[x]C1 * freq[y]C1 * freq[x + y]C1, as among all possible frequencies of x, y and x + y, we just need to consider the triplet containing all x, y and x + y.

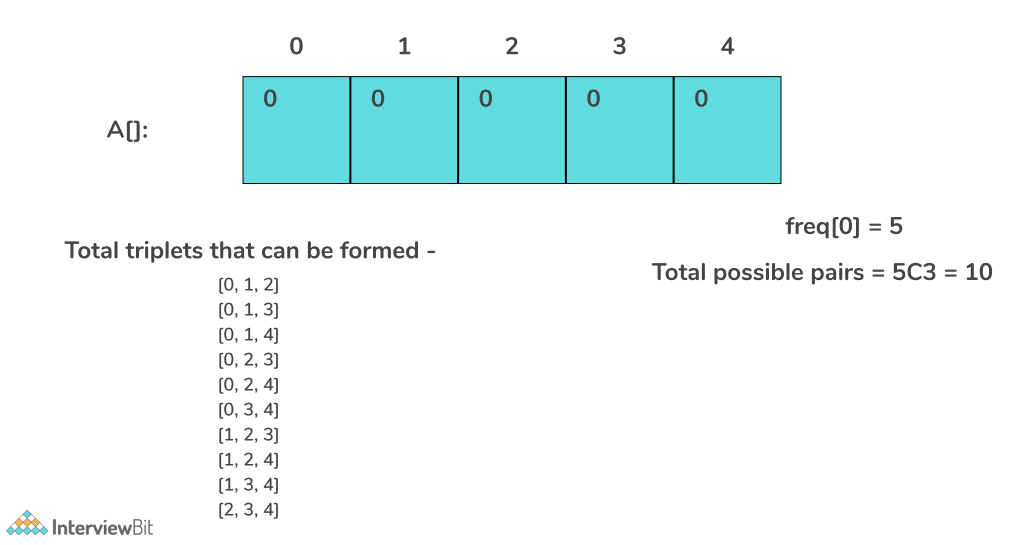
Algorithm

• Compute the value of the maximum element, mx of the array.
• Build a frequency array, freq of size mx + 1 and store the frequency of all the elements of the array A[].
• Initialise a count variable and consider the above four cases one by one:
  • If the triplet is (0, 0, 0), add freq[0]C3 to count.
  • If the triplet is (0, x, x), add freq[0]C1 * freq[x]C2 to count.
  • If the triplet is (x, x, 2x), add freq[x]C2 * freq[2x]C1 to count.
  • If the triplet is (x, y, x + y), add freq[x]C1 * freq[y]C1 * freq[x + y]C1 to count.
• Return count.

C++ Code For Hashing Method

Java Code For Hashing Method

Python Code For Hashing Method

Time Complexity: O(N^2) where N is the number of nodes of the binary tree.
Space Complexity: O(N), as a map is used.

Practice Questions

Maximum Sum Triplets
3 Sum Zero

Frequently Asked Questions

How do you count triplets in an array?
The triplets can be counted by running three nested loops over the size of the array.

What are triplets in an array?
The triplet of an array is a tuple of three elements of different indices, represented by (i, j, k).