Delete Node From Binary Search Tree

Problem Statement

Given a binary search tree and a key value. The task is to delete the given key from the BST and return the updated root node.

Examples:
Input:

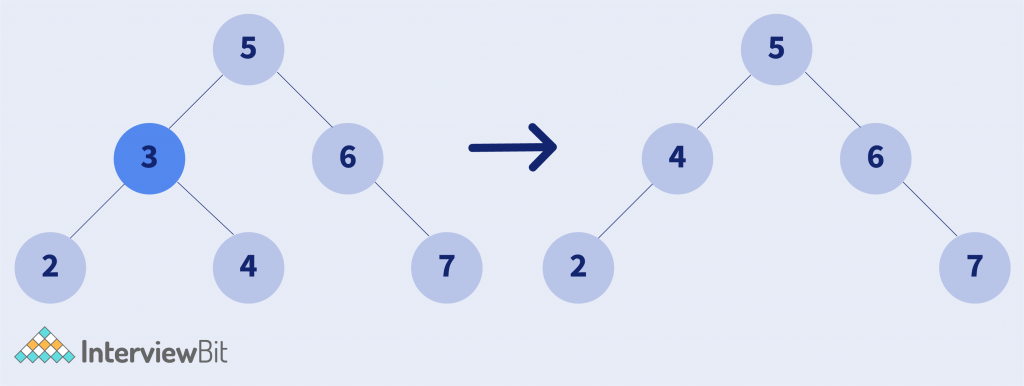
Key = 3
Output: Shown in the image

Approach: Recursion

If you observe clearly, there are mainly three possible conditions.

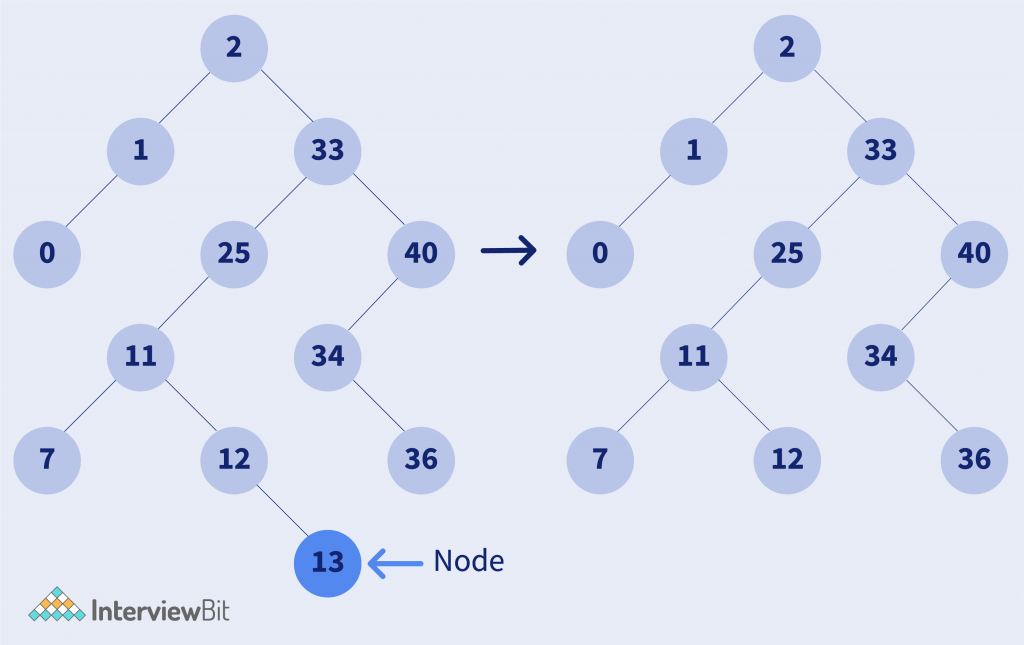
Case 1:

• If the key to be deleted is a leaf node:
  • In this case, simply make the node NULL.

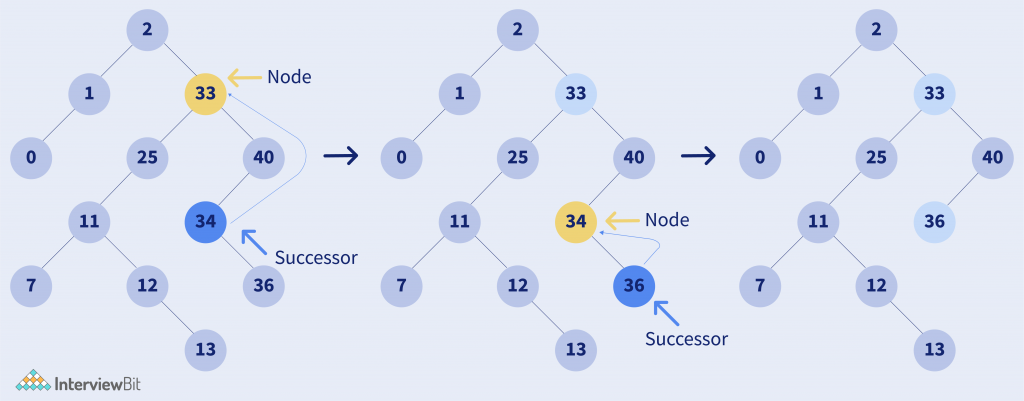
Case 2:

• If the key to be deleted is not a leaf and has the right child.
  • In this case, replace the node with its successor node.

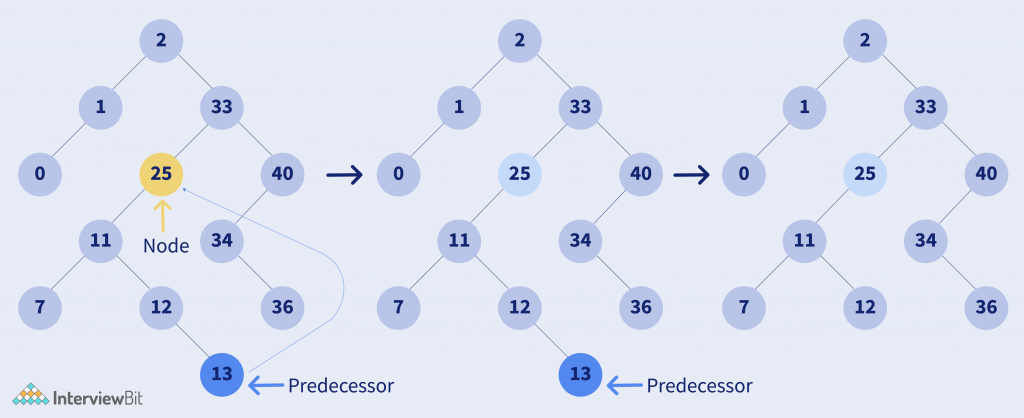
Case 3:

• If the key to be deleted is not a leaf and has a left child and no right child.
  • In this case, replace the node with its predecessor node.

Algorithm

• Compare the value of the key with the value of the root. If the key > root -> value, recursively traverse the right subtree.
• If key < root -> value, recursively traverse the left subtree.
• While traversing if key == root->value, we need to delete this node:
  • If the node is a leaf, make root = NULL.
  • If the node is not a leaf and has the right child, recursively replace its value with the successor node and delete its successor from its original position.
  • If the node is not a leaf and has a left child, but not a right child, recursively replace its value with a predecessor node and delete its predecessor from its original position.
• Return root

Implementation

C++ Code

int successor(TreeNode * root) {
  root = root -> right;
  while (root -> left != NULL) root = root -> left;
  return root -> val;
}
int predecessor(TreeNode * root) {
  root = root -> left;
  while (root -> right != NULL) root = root -> right;
  return root -> val;
}
 
TreeNode * deleteNode(TreeNode * root, int key) {
  if (root == NULL) return NULL;
  if (key > root -> val) root -> right = deleteNode(root -> right, key);
  else if (key < root -> val) root.left = deleteNode(root -> left, key);
  else {
    if (root -> left == NULL && root -> right == NULL) root = NULL;
    else if (root -> right != NULL) {
      root -> val = successor(root);
      root.right = deleteNode(root -> right, root -> val);
    } else {
      root -> val = predecessor(root);
      root -> left = deleteNode(root -> left, root -> val);
    }
  }
  return root;
}

Java Code

int successor(TreeNode * root) {
  root = root -> right;
  while (root -> left != NULL) root = root -> left;
  return root -> val;
}
int predecessor(TreeNode * root) {
  root = root -> left;
  while (root -> right != NULL) root = root -> right;
  return root -> val;
}
 
TreeNode * deleteNode(TreeNode * root, int key) {
  if (root == NULL) return NULL;
  if (key > root -> val) root -> right = deleteNode(root -> right, key);
  else if (key < root -> val) root.left = deleteNode(root -> left, key);
  else {
    if (root -> left == NULL && root -> right == NULL) root = NULL;
    else if (root -> right != NULL) {
      root -> val = successor(root);
      root.right = deleteNode(root -> right, root -> val);
    } else {
      root -> val = predecessor(root);
      root -> left = deleteNode(root -> left, root -> val);
    }
  }
  return root;
}
}

Python Code

class Solution:
    def successor(self, root):
        root = root.right
        while root.left:
            root = root.left
        return root.val
 
    def predecessor(self, root):
        root = root.left
        while root.right:
            root = root.right
        return root.val
 
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return None
 
        if key > root.val:
            root.right = self.deleteNode(root.right, key)
        elif key < root.val:
            root.left = self.deleteNode(root.left, key)
        else:
            if not (root.left or root.right):
                root = None
            elif root.right:
                root.val = self.successor(root)
                root.right = self.deleteNode(root.right, root.val)
            else:
                root.val = self.predecessor(root)
                root.left = self.deleteNode(root.left, root.val)
 
        return root

Time Complexity: O(logN), where N is the number of nodes.
Space Complexity: O(H), for recursion stack, where H is the height of the BST.

FAQs

Q.1: Why is the time complexity log(N)?

Ans. Since the given tree is a BST, we need to traverse the right subtree or left subtree at any given point. Hence, the time complexity is log(N).

Q.2: What is the most efficient approach to solving this problem?

Ans. The recursive approach is the most efficient approach to solving the problem. The time complexity is O(logN) and the space complexity is O(H).