In the world of programming, there are two main approaches to solving problems; greedy and dynamic programming. Greedy programming is the approach that tries to solve a problem as quickly as possible, while dynamic programming is the approach that tries to solve a problem as efficiently as possible.
In greedy programming, you try to solve a problem as quickly as possible by trying to find the smallest possible solution. In dynamic programming, you try to solve a problem as efficiently as possible by trying to find the smallest possible solution. Both approaches have their advantages and disadvantages. Greedy programming can be very time-consuming if you are trying to solve a very large problem, but it can also be very efficient if you are trying to solve a small problem. On the other hand, dynamic programming can be very time-consuming if you are trying to solve a very small problem, but it can also be very efficient if you are trying to solve a large problem.
As a general rule, dynamic programming is better than greedy programming when you are solving problems that involve large numbers of variables or when you are solving problems that involve a lot of data. On the other hand, greedy programming is better than dynamic programming when you are solving problems that involve small numbers of variables or when you are solving problems that involve a lot of data. A dynamic programming algorithm is a powerful tool that can be used to solve problems more efficiently than other algorithms.
Confused about your next job?
In this blog post, we’ll take a closer look at greedy vs dynamic programming algorithms. We’ll see why using these two methods is important when writing software and how they are different. We’ll also explore best practices for choosing between them.
What is the Greedy Method?
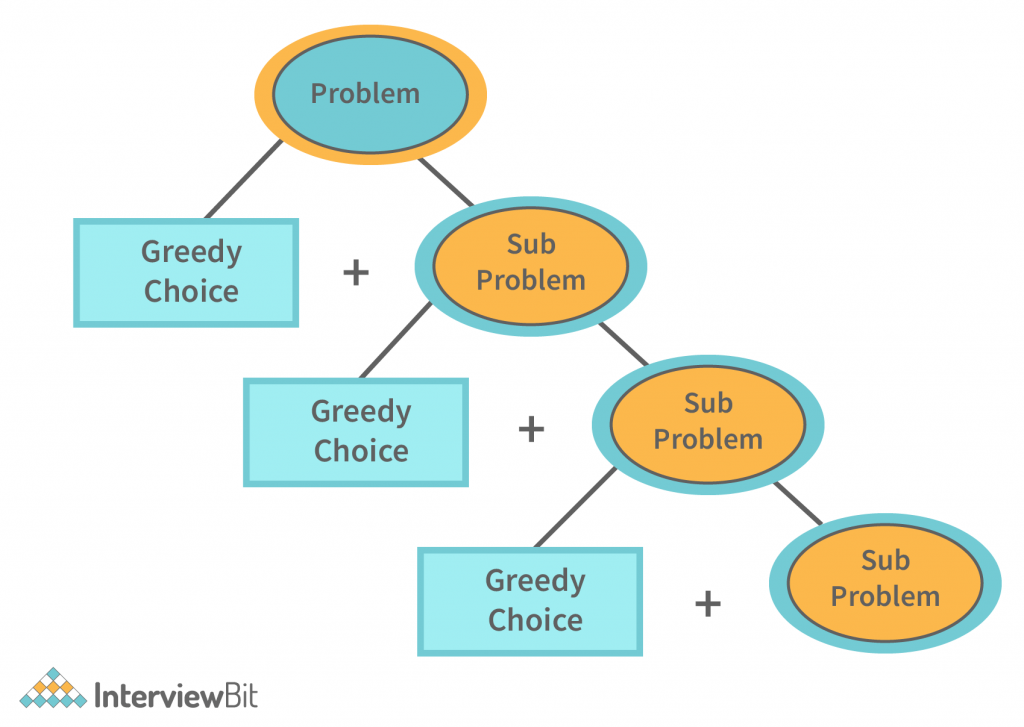
The greedy approach is used to answer problems involving optimization. It is a strategy that focuses on obtaining the maximum or minimum result. We can better understand the term problem with a few terms. The simplest and most straightforward method is the Greedy method. It is not an algorithm but a technique. The decision is made on the basis of current information only, regardless of future impact. This method determines whether or not an optimal solution is possible. The meet-specified criterion is a subset that contains only the best and most beneficial solutions. In the event of a feasible solution, if more than one solution satisfies the condition, then those solutions will be accepted as feasible, whereas the best solution will be the only one among all of them.
What is Dynamic Programming?
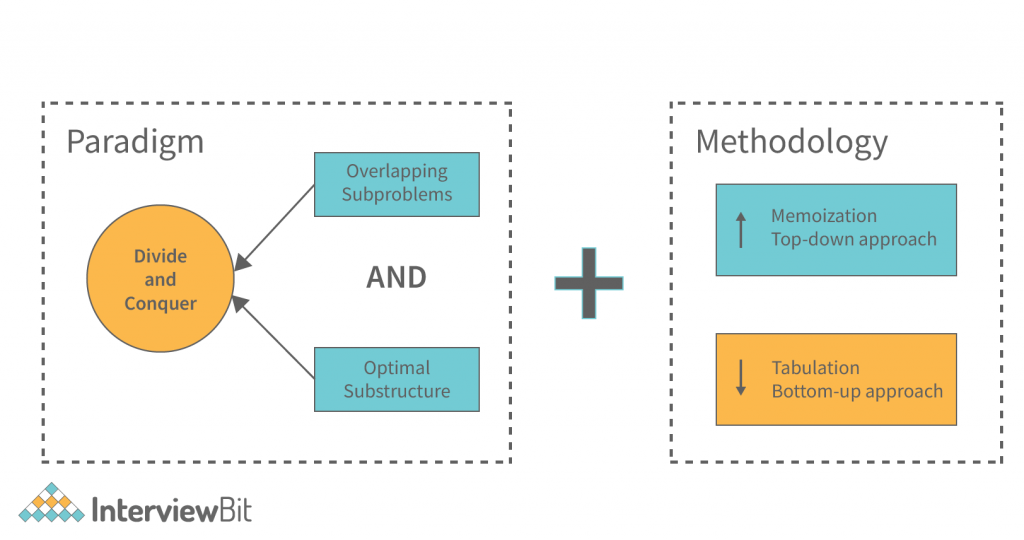
Whenever we encounter a recursive form that has identical inputs for repeated uses, we can lower time complexity using dynamic programming. We may save the results of subproblems by recording them. This minimal optimization reduces time complexity to a polynomial ratio. For example, if we recorded all the answers to the Fibonacci summation, time complexity would be reduced to linear. If we recorded subproblems, time complexity would be reduced to linear. Dynamic programming is a programming technique that allows programmers to solve problems in a way that takes into account the impact of variables and other factors on the solution. The basic idea is to break down a problem into smaller, more manageable pieces and then solve each of those pieces separately. This approach lets programmers avoid the overhead of calculating large, complicated expressions, and it also allows them to make decisions more quickly. When applied to problems with more than one variable, dynamic programming can be used to solve problems that are difficult to analyze or predict. Dynamic programming can be used in a variety of situations, including optimization, regression analysis, and optimization.
Dynamic programming is a powerful optimization algorithm that can be used to solve a wide variety of problems. One of its most important features is memoization, which allows it to quickly solve problems that require large amounts of data. In dynamic programming, the goal is to minimize the worst-case time to solve a problem. The simplest way to achieve this is to keep track of the data that needs to be processed and only process the data as it becomes available. However, this approach can be expensive and inefficient, so it’s often better to use memoization instead.
When using memoization, the algorithm is first asked to find the best possible solution for a given problem. If there is no solution, the algorithm is told to keep trying until it finds one. Once it finds a solution, it can use that solution to solve any subsequent problems that are encountered. The main advantage of memoization over keeping track of all the data is that it’s much easier to keep track of only what you need. This makes it much easier to process large amounts of data quickly and efficiently. The downside of memoization is that it’s not always possible or efficient to use it in all situations. For example, if you’re dealing with very large amounts of data, it’s likely that you’ll run into memory problems and will need to use some other optimization technique instead.
We use the DP algorithms and tabulation techniques to achieve the DP goals. We also call them bottom-up approaches. The method begins with solving the lowest level subproblem, then the next level, and so on. We solve all the subproblems in sequence until we come up with all of them. This saves time when a problem has a solution not yet been discovered.
Key Differences
A list of differences between the greedy method and dynamic programming is provided.
- While dynamic programming produces hundreds of decision sequences, the greedy method produces only one.
- Using dynamic programming, you can achieve better results than using greedy programming.
- In dynamic programming, the top-down approach is used, whereas, in the greedy method, the bottom-up approach is used.
- A dynamic program may involve any number of secondary subproblems and may produce an optimal solution, in contrast to an efficient algorithm, which may require only a unique set of feasible sets of solutions.
- A greedy algorithm is one that tries to solve a problem by trying different solutions. It is usually faster than a dynamic program and more expensive than a greedy programming approach.
- A method that lacks the power to deal with overlapping problems is successful at handling them, whereas a dynamic programming approach successfully handles them.
- In dynamic programming, the solution to a problem is evaluated based on how well it performs in the future. In contrast, in greedy programming, the solution is evaluated based on how well it performs in the current situation.
- Greedy programming is a programming style that involves making decisions based on the current state of the program. In contrast, dynamic programming is a programming style that involves making decisions based on the future state of the program.
- Dynamic programming algorithms are often used in situations where the solution to a problem is not known in advance. For example, if you have to make a decision based on incomplete information, you may want to use a dynamic programming algorithm instead of a greedy algorithm. In contrast, greedy algorithms are often used when you know the solution to a problem ahead of time. For example, if you have to make a decision based on a set of rules that you know ahead of time, you may want to use a greedy algorithm instead of a dynamic programming algorithm.
- Greedy algorithms are often used in situations where there is a limited amount of information available. For example, a greedy algorithm might be used to solve a problem in which the number of possible solutions is limited. In contrast, dynamic programming is typically used when there is more information available. For example, a dynamic programming algorithm might be used when there are multiple possible solutions to a problem.
Difference Between Greedy and Dynamic Programming
There are several key differences between the greedy method and dynamic programming, listed below:
| Greedy Programming | Dynamic Programming |
| A greedy algorithm chooses the best solution at the moment, in order to ensure a global optimal solution. | In dynamic programming, we look at the current problem and the current solution to determine whether to make a particular choice or not. We then calculate the optimal choice based on previous problems and solutions. |
| It is not guaranteed that an optimal solution will be obtained in the greedy method. | Because of the nature of Dynamic Programming, it is certain that an optimal solution will be generated. |
| A greedy methodology follows the problem-solving approach of making the locally optimal choice at each step. | Dynamic programming is an algorithmic approach that uses a recurring formula to calculate new states. |
| The process of looking back and revisiting previous choices is more costly in terms of memory. | The memoization solution requires a DP table, which increases memory complexity. |
| It is easier to engage in greedy procedures than to use Dijkstra’s shortest path algorithm, which takes O(ElogV + VLogV) time. | Bellman-Ford algorithm, which is based on dynamic programming, takes O(V) time. |
| The greedy approach deterministically obtains its answer by repeatedly selecting a random step in a backward direction and never looking back or changing previous choices. | Developing a solution top-down or bottom-up is accomplished by obtaining smaller optimal sub-solutions. |
| Fractional knapsack is an example of greedy algorithms. | 0/1 knapsack problem is an example of greedy algorithms. |
| Every problem can’t be solved by a greedy algorithm. | Every problem can be solved by a Dynamic algorithm. |
| A solution to a specified problem set is contained within the given solution set. | It is not necessary to insist on a particular set of feasible solutions. |
| More Efficient because we never look back to other options. | Less Efficient as compared to a greedy approach because it’s required a DP table to store the answers of calculated states. |
| A set of overlapping problems cannot be dealt with. | A set of overlapping problems can be dealt with. |
| No memorization is required. | Memorization is required. |
| A greedy strategy is faster than a dynamic one. | Compared to greedy programming, it is slower. |
| Fast results. | Slow results comparatively. |
| Each step is locally optimal. | Past solutions are used to create new ones. |
Conclusion
In the dynamic programming approach, the goal is to minimize the number of steps required to reach a given goal. The basic idea is to find a way to break down a problem into smaller pieces and then solve each piece individually. The problem is then solved in the most efficient way possible. In contrast, the greedy approach focuses on maximizing the overall amount of work that can be done. This approach is often used when there is not enough information available to make a decision. The goal is to find a way to minimize the number of steps required. Dynamic programming is a powerful tool that can be used in many different situations. It can be used to solve problems that are difficult to solve using other methods. It can also be used when there is not enough information available to make a decision.
FAQs:
Q.1: Where is the greedy algorithm used?
Ans: A greedy algorithm is one that uses a large number of small steps to achieve a larger objective. Artificial intelligence (AI) uses them to master data. The primary objective of greedy algorithms is to reduce the amount of work that needs to be done, while still obtaining the highest possible outcome. The basic idea is starting with a few feasible choices and working your way up to the best. This may be time-consuming, so greedy algorithms are often used to learn from data in practice.
Q.2: What is a dynamic programming example?
Ans: Dynamic programming is a mathematical technique that addresses difficulties. It is based on the notion that you can approach a difficulty by considering different approaches. The tool is dynamic because it changes as your thinking changes. You can find the best answer to a difficulty using dynamic programming. It can be used to determine the best matches for a variety of reasons. It may also be used to determine the best solution to a problem with unknown variables or proportions. It may also provide the best solution to a problem in which there are many options. Dynamic programming is commonly utilised in machine learning and optimization techniques. Knapsack questions are an example of dynamic programming.
Q.3: Why do we use Dynamic Programming?
Ans: A programming technique that can be used to discover optimal solutions to difficult problems is dynamic programming. It is frequently applied in computer science and engineering to determine the optimum solution to difficult problems. A problem is first formulated as a set of constraints, and then a solution is determined by solving the constraints in an iterative manner. It is not always the best possible solution to a problem, rather it’s a trade-off between the cost of making one modification and the cost of making another modification. If you are forced to make two modifications to your variable at the same time, for instance, it makes sense to choose the second option. Dynamic programming may be used to find the best solution to a problem.
Q.4: What are the advantages of the Greedy Algorithm?
Ans: The main advantage of greedy algorithms is that they can be used to solve a wide variety of problems. They can be used to find the shortest route in a network or to recommend the most efficient route for a vehicle. They are also very easy to implement. Because of this, greedy algorithms are very effective at solving a lot of problems. One issue with greedy algorithms, however, is that they are very difficult to design. In addition, greedy algorithms are very effective at solving a lot of problems, but they are quite speedy. Because of this, they may be used to solve a variety of issues.




