Problem Statement
Given two strings A and B, find the minimum number of steps required to convert A to B. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
- Insert a character
- Delete a character
- Replace a character
Examples:
Confused about your next job?
Input: A = “abad”, B = “abac”
Output: 1
Explanation: Operation 1: Replace d with c.
Input: A = “horse”, B = “ro”
Output: 3
Approach 1: Recursion
The idea is to use a recursive approach to solve the problem.
All the characters of both the strings are traversed one by one either from the left or the right end and apply the given operations.
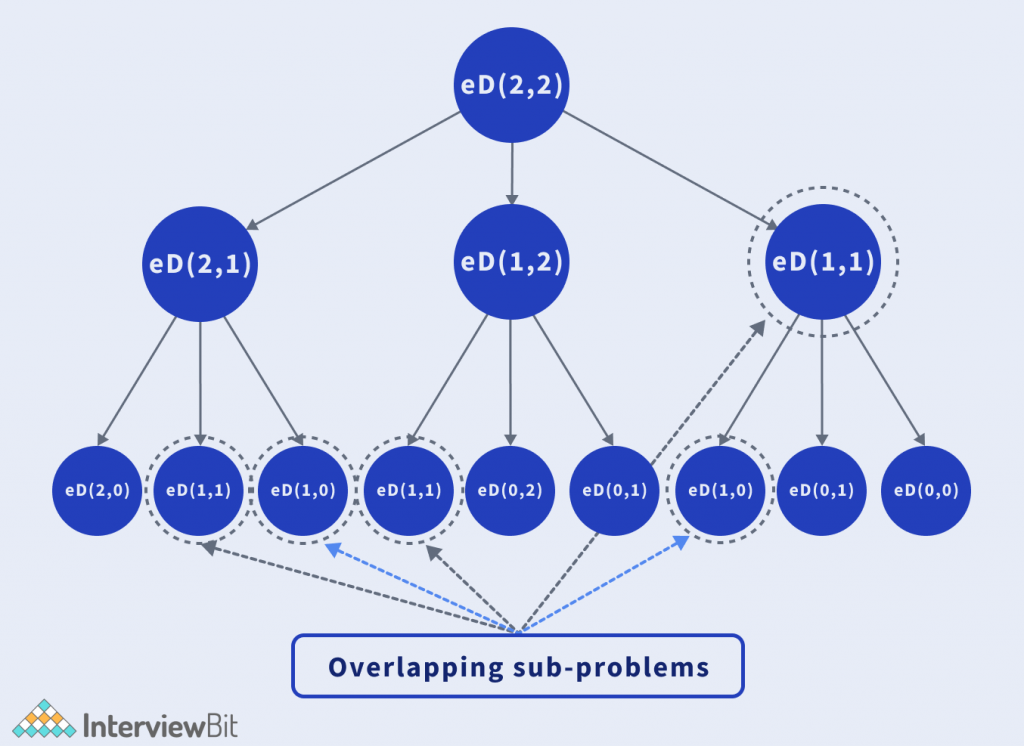
Algorithm:
- Consider two pointers i and j pointing the given string A and B.
- If the current character, pointing in both the strings are same, then no changes are to be made. Therefore, recurse for lengths i + 1 and j + 1.
- Otherwise, try to apply the free operations provided.
- Each of the given operations would cause 1 units.
- The character pointer i points to is A[i] and pointer j is B[j]. Therefore, F(i, j ) is the edit distance of A(0,i) and B(0, j).
- For insertion: Recurse i – 1 to j.
- For deletion: Recurse i to j – 1.
- For replacement: Recurse i – 1 to j – 1.
- After applying all the operations, f(i, j) = 1 + min(f(i – 1, j), f(i, j – 1), f(i – 1, j – 1)).
C++ Implementation
int editDistanceHelper(int i, int j, string & str1, string & str2) {
if (i == 0) {
return j;
}
if (j == 0) {
return i;
}
int ans = 1 + min({
editDistanceHelper(i, j - 1, str1, str2), // Insert
editDistanceHelper(i - 1, j, str1, str2), // Remove
editDistanceHelper(i - 1, j - 1, str1, str2) // Replace
});
if (str1[i - 1] == str2[j - 1]) {
ans = min(ans, editDistanceHelper(i - 1, j - 1, str1, str2));
}
return ans;
}
int editDistance(string str1, string str2) {
int n = str1.size() + 1, m = str2.size() + 1;
int ans = editDistanceHelper(n, m, str1, str2);
return ans;
}Java Implementation
private static int editDistanceHelper(int i, int j, String str1, String str2) {
if (i == 0) {
return j;
}
if (j == 0) {
return i;
}
int ans = 1 + Math.min(Math.min(
editDistanceHelper(i, j - 1, str1, str2), // Insert
editDistanceHelper(i - 1, j, str1, str2)), // Remove
editDistanceHelper(i - 1, j - 1, str1, str2) // Replace
);
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
ans = Math.min(ans, editDistanceHelper(i - 1, j - 1, str1, str2));
}
return ans;
}
public static int editDistance(String str1, String str2) {
int n = str1.length(), m = str2.length();
int ans = editDistanceHelper(n, m, str1, str2);
return ans;
}Python Implementation
def editDistanceHelper(i, j, str1, str2):
if i == 0:
return j
if j == 0:
return i
ans = 1 + min(
{
editDistanceHelper(i, j - 1, str1, str2), # Insert
editDistanceHelper(i - 1, j, str1, str2), # Remove
editDistanceHelper(i - 1, j - 1, str1, str2), # Replace
}
)
if str1[i - 1] == str2[j - 1]:
ans = min(ans, editDistanceHelper(i - 1, j - 1, str1, str2))
return ans
def editDistance(str1, str2):
n = len(str1)
m = len(str2)
ans = editDistanceHelper(n, m, str1, str2)
return ansTime Complexity:O(3^(N * M)), where N and M is the length of the first and second string.
Space Complexity:O(N + M), where N and M is the length of the first and second string.
Efficient Approach: Dynamic Programming
The idea is to use a dynamic programming approach here. The tabulation method is the most efficient method to solve this problem.

As stated earlier, since the problem has overlapping subproblems, many of the calculations are repeated.
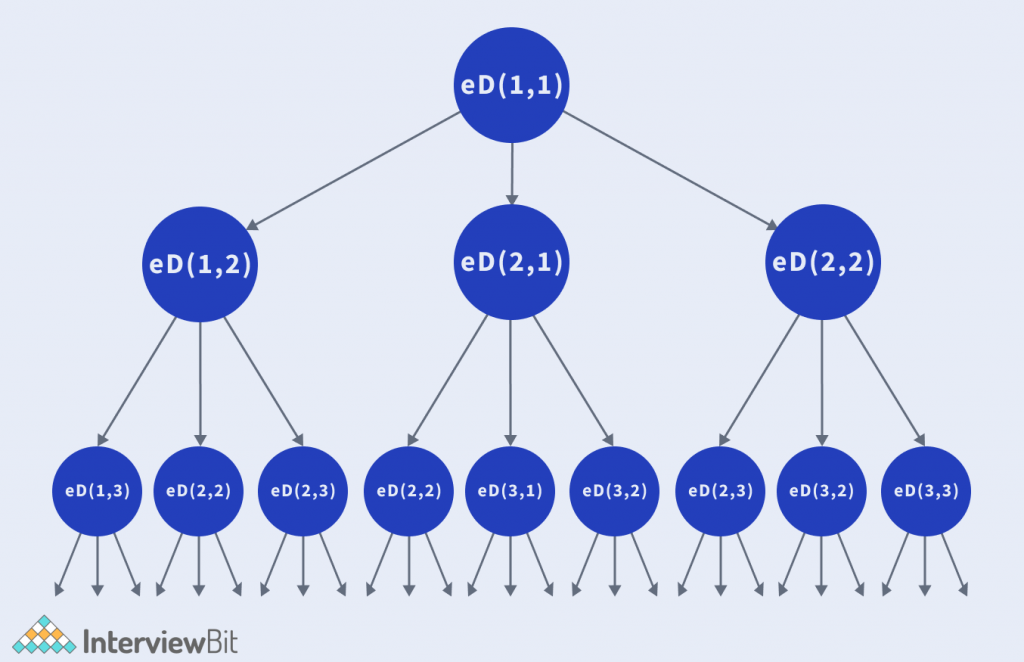
Algorithm:
- Initialise a 2D dp, where dp[i][j] denotes the edit distance of the length (i + 1)th of A and (j + 1)th length of B.
- The recurrence relation is as follows:

- If current character of both the strings are same:dp[i][j] = dp[i – 1][j – 1]
- If current character of both the strings are different:dp[i][j] = 1 + min(dp[i – 1][j – 1], dp[i – 1][j], dp[i][j – 1])
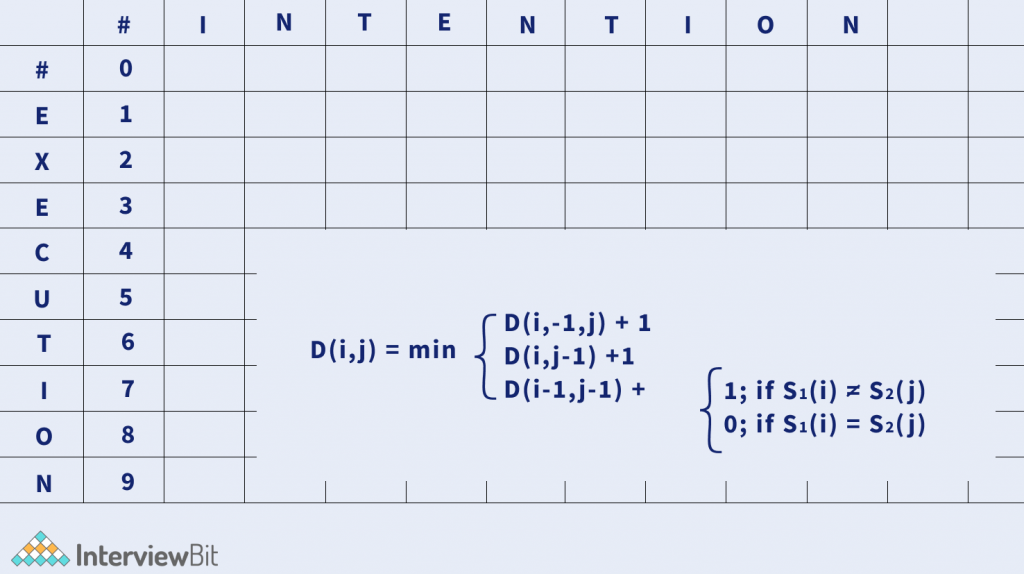
Let us understand this by an example :
This example dry runs all the possible edit distances of the two words HORSE and ROS.

Similarly, the tabular computations are done as follows :
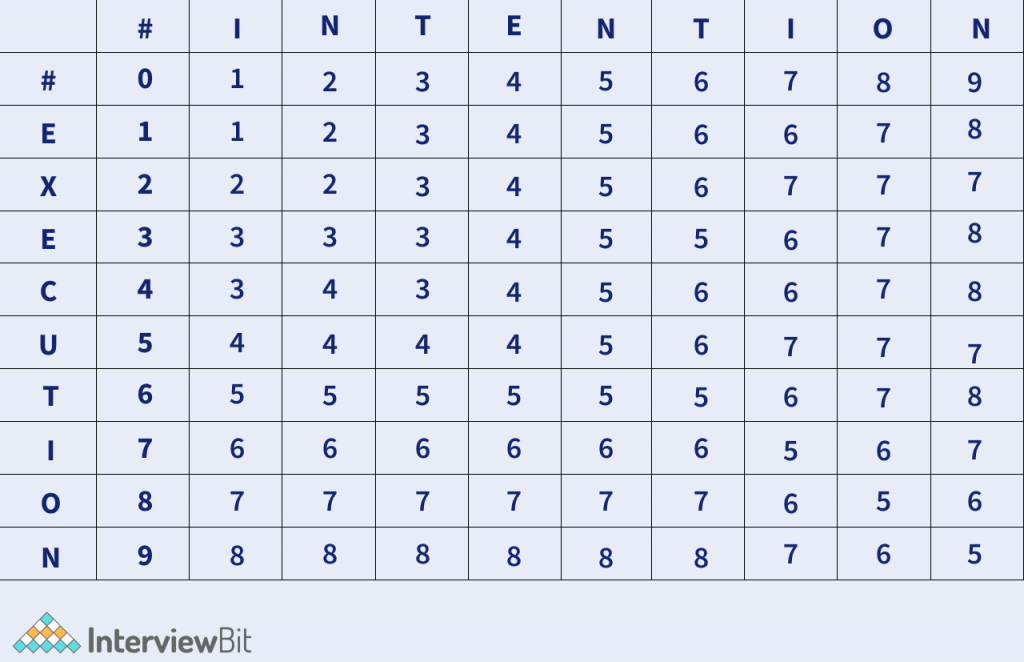
C++ Implementation
int editDistance(string str1, string str2)
{
int n = str1.size(), m = str2.size();
int **dp = new int *[n + 1];
for (int i = 0; i <= n; i++)
{
dp[i] = new int[m + 1];
}
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= m; j++)
{
if (i == 0)
{
dp[i][j] = j;
}
else if (j == 0)
{
dp[i][j] = i;
}
else if (str1[i - 1] == str2[j - 1])
{
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = 1 + min(min(dp[i][j - 1],
dp[i - 1][j]),
dp[i - 1][j - 1]);
}
}
}
int ans = dp[n][m];
for (int i = 0; i <= n; i++)
{
delete[] dp[i];
}
delete[] dp;
return ans;
}Java Implementation
public static int editDistance(String str1, String str2)
{
int n = str1.length(), m = str2.length();
int[][] dp = new int [n + 1][m + 1];
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= m; j++)
{
if (i == 0)
{
dp[i][j] = j;
}
else if (j == 0)
{
dp[i][j] = i;
}
else if (str1.charAt(i - 1) == str2.charAt(j - 1))
{
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = 1 + Math.min(Math.min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]);
}
}
}
int ans = dp[n][m];
return ans;
}Python Implementation
INT_MAX = 10000000
def editDistance(str1, str2):
n = len(str1)
m = len(str2)
dp = [[INT_MAX for i in range(m + 1)] for j in range(n + 1)]
for i in range(n + 1):
for j in range(m + 1):
if i == 0:
dp[i][j] = j
elif j == 0:
dp[i][j] = i
elif str1[i - 1] == str2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
dp[i][j] = 1 + min(min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1])
ans = dp[n][m]
return ansTime Complexity:O(N * M), where N and M is the length of the first and second string.
Space Complexity: O(N * M), where N and M is the length of the first and second string.
Practice Question
FAQs
Q.1: What is the edit distance problem?
Ans: The edit distance problem is the minimum number of insertions, deletions, or replacements required to convert one string to another.
Q.2: What is the time and space complexity of the dynamic programming approach?
Ans: The time and space complexity of the dynamic programming approach is O(N * M)




