Dijkstra’s Shortest Path Algorithm

Problem Statement

You are given an undirected graph ( assume with N nodes and M edges)  and each edge has some non-negative weight you are also given some source node S and you have to find the shortest path from starting node(vertex) S to all other nodes.

Here the shortest path means the sum of the weight of edges should be minimum in that path.

Examples:

Input: 

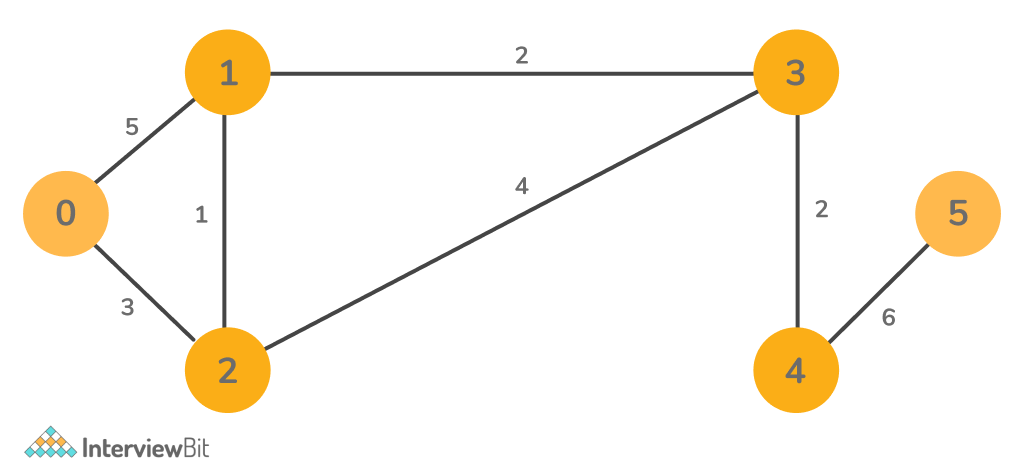
Output: 

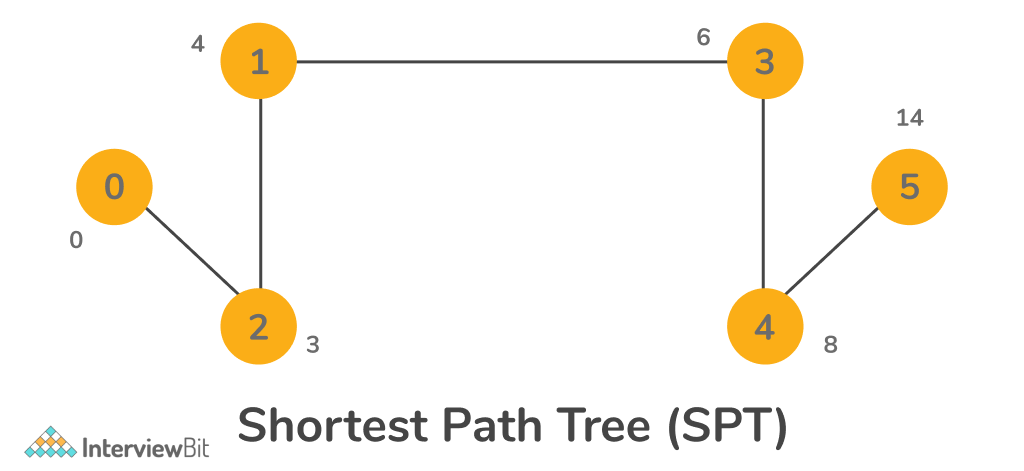
Explanation :

0–>0 : distance = 0  Path : 0
0–>0 : distance = 4 Path :0 2 1
0–>0 : distance = 3 Path : 0 2
0–>0 : distance = 6 Path : 0 2 1 3 
0–>0 : distance = 8 Path : 0 2 1 3 4
0–>0 : : distance = 14 Path : 0 2 1 3 4 5

INPUT: 

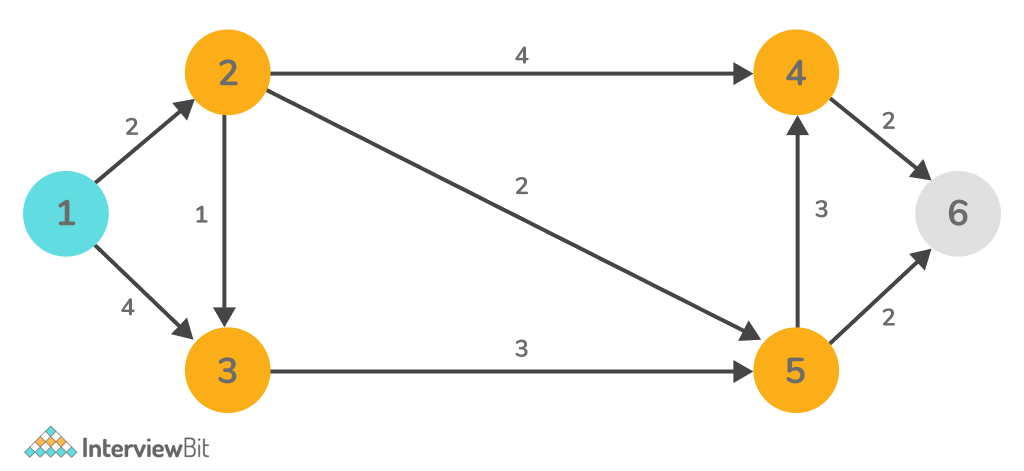
OUTPUT: 

Shortest path between 1 to 6 is 6 
Path : 1 -> 2 -> 5 -> 6

INTUITION:

The first thought which comes to our mind is that find all the paths and then we can compare all the paths and the path which is giving minimum cost then we will choose that path. This approach is absolutely correct but this approach to finding all the paths will increase the complexity.

So to decrease the time complexity, we can take advantage of the fact that if there are multiple edges from a node to another node then we can always choose the edge which is of minimum weight. Hence if we will come to any node with less cost then we will always choose that path. And for finding the minimum edges among all the edges we can use any data structure such as a priority queue.

Code: Dijkstra Algorithm 

Approach

1. Set the distance of the source node to 0 and initially, all the vertices are at distances at infinity.
2. Maintain the visited array so that we can maintain the status of all the vertices.
3. Now mark the current vertex as visited( which is the source node)
4. Now the vertices which are adjacent to the present vertex, update all the distance from the source vertex which is equal to the minimum of its current distance and the sum of the weight of the current edge.
5. Now the vertex which is unvisited, set one as the new current vertex and do the same thing as above to check if the node has minimum distance till now or if it is not then update it with the summation of the current node distance and current edge weight.
6. Repeat steps 3-5 until all vertices are flagged as visited.

C++ Code Implementation

bool mark[MAXN];
void dijkstra(int v) {
  fill(d, d + n, inf);
  fill(mark, mark + n, false);
  d[v] = 0;
  int u;
  priority_queue < pair < int, int > , vector < pair < int, int > > , less < pair < int, int > > > pq;
  pq.push({
    d[v],
    v
  });
  while (!pq.empty()) {
    u = pq.top().second;
    pq.pop();
    if (mark[u])
      continue;
    mark[u] = true;
    for (auto p: adj[u]) //adj[v][i] = pair(vertex, weight)
      if (d[p.first] > d[u] + p.second) {
        d[p.first] = d[u] + p.second;
        pq.push({
          d[p.first],
          p.first
        });
      }
  }
}

Java Code Implementation

public class Dijkstra {

  public static void dijkstra(int[][] graph, int source) {
    int count = graph.length;
    boolean[] visitedVertex = new boolean[count];
    int[] distance = new int[count];
    for (int i = 0; i < count; i++) {
      visitedVertex[i] = false;
      distance[i] = Integer.MAX_VALUE;
    }

    // Distance of self loop is zero
    distance[source] = 0;
    for (int i = 0; i < count; i++) {

      // Update the distance between neighbouring vertex and source vertex
      int u = findMinDistance(distance, visitedVertex);
      visitedVertex[u] = true;

      // Update all the neighbouring vertex distances
      for (int v = 0; v < count; v++) {
        if (!visitedVertex[v] && graph[u][v] != 0 && (distance[u] + graph[u][v] < distance[v])) {
          distance[v] = distance[u] + graph[u][v];
        }
      }
    }
    for (int i = 0; i < distance.length; i++) {
      System.out.println(String.format("Distance from %s to %s is %s", source, i, distance[i]));
    }

  }

  // Finding the minimum distance
  private static int findMinDistance(int[] distance, boolean[] visitedVertex) {
    int minDistance = Integer.MAX_VALUE;
    int minDistanceVertex = -1;
    for (int i = 0; i < distance.length; i++) {
      if (!visitedVertex[i] && distance[i] < minDistance) {
        minDistance = distance[i];
        minDistanceVertex = i;
      }
    }
    return minDistanceVertex;
  }
}

Python Code

def dijkstra(self, times: List[List[int]], N: int, K: int) -> int:
    graph = collections.defaultdict(list)
    for (u, v, w) in times:
        graph[u].append((v, w))

    priority_queue = [(0, K)]
    shortest_path = {}
    while priority_queue:
        w, v = heapq.heappop(priority_queue)
        if v not in shortest_path:
            shortest_path[v] = w
            for v_i, w_i in graph[v]:
                heapq.heappush(priority_queue, (w + w_i, v_i))

    if len(shortest_path) == N:
        return max(shortest_path.values())
    else:
        return -1

Time Complexity: O(ELogV) where E is the number of edges and V is the number of vertices.
Space Complexity: O(V)

Practise Problem

• Delete Edge

FAQs

Q.1: What is Dijkstra’s Shortest Path Algorithm?

Ans: From this Algorithm, we can find the shortest path from any source node to all other nodes.

Q.2: How to Implement the Dijkstra Algorithm?

Ans: We can implement this algorithm by using a priority queue or any STL which is capable of finding the minimum element from the array in log n and the array is changing each second.