GCD of Two Numbers (C, Python, Java) With Examples

Problem Statement

Given two non-negative integers a and b, we have to find their GCD (greatest common divisor),i.e. the largest number which is a divisor of both a and b. It’s commonly denoted by
gcd(a,b). Mathematically it is defined as

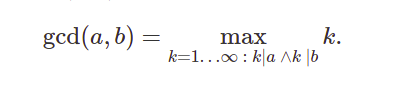
Example:

Input: a=32, b=20
Output: 4
Explanation: 4 is the largest factor that divides both of the numbers.

Input: a=98, b=70
Output: 14
Explanation: 14 is the largest factor that divides both of the numbers.

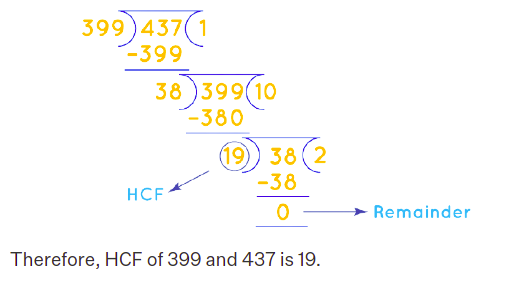
Input: a=399, b=437
Output: 19
Explanation:

Simple Approach

We can traverse over all the numbers from min(A, B) to 1 and check if the current number divides both A and B or not. If it does, then it will be the GCD of A and B.

C++ Implementation

int GCD(int A, int B) {
    int m = min(A, B), gcd;
    for(int i = m; i > 0; --i)
        if(A % i == 0 && B % i == 0) {
            gcd = i;
            return gcd;
        }
}

Python Implementation

def GCD_Loop( a, b):  
    if a > b:  # define the if condition  
        temp = b  
    else:  
        temp = a  
    for i in range(1, temp + 1):  
        if (( a % i == 0) and (b % i == 0 )):  
            gcd = i  
    return gcd 

Java Implementation

class Main {
  public static void main(String[] args) {

    // find GCD between n1 and n2
    int n1 = 81, n2 = 153;
    
    // initially set to gcd
    int gcd = 1;

    for (int i = 1; i <= n1 && i <= n2; ++i) {

      // check if i perfectly divides both n1 and n2
      if (n1 % i == 0 && n2 % i == 0)
        gcd = i;
    }

    System.out.println("GCD of " + n1 +" and " + n2 + " is " + gcd);
  }
}

Time complexity: O(min(A, B))
Space complexity: O(1)

Efficient Approach: Euclid’s Algorithm

The algorithm is based on the below facts.

• When we have to reduce a larger number then what we can do in a simple manner is just subtract small numbers from larger numbers and from this we can notice GCD will not change. Hence we can keep subtracting the larger of two numbers, we end up with the GCD.
• Now instead of doing subtraction, we can do one more thing i.e if we divide the smaller number, the algorithm stops when we find remainder 0.

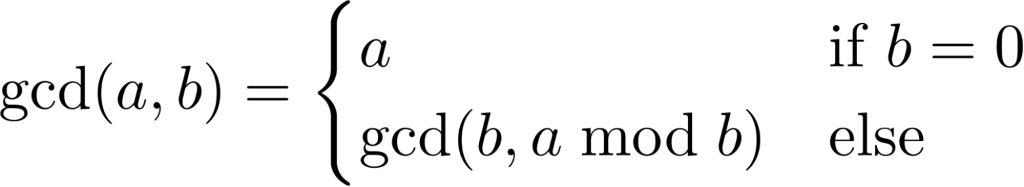
C/C++ Implementation of Efficient Approach

// Function to return
// gcd of a and b
int gcd(int a, int b) {
  if (a == 0)
    return b;
  return gcd(b % a, a);
}

Java Implementation of Efficient Approach

import java.util.*;
import java.lang.*;

class Interviewbit {
  // extended Euclidean Algorithm
  public static int gcd(int a, int b) {
    if (a == 0)
      return b;

    return gcd(b % a, a);
  }

}

Python Implementation of Efficient Approach

def gcd(a, b):
	if a == 0 :
		return b
	
	return gcd(b%a, a)

Time complexity: O(Log min(a, b)) where ‘a’ and ‘b’ are two numbers.
Space complexity: O(1)

Practice Questions

• Solve Problem: Greatest Common Divisor
• Largest Coprime Divisor
• GCD CMPL

Frequently Asked Questions

Q1: How do you find the GCD of two numbers?

Ans: From the Euclidean algorithm as it has less time complexity (log(min(a,b))

Q2: Can we find the GCD of negative numbers?

Ans: Yes, GCD(6, -12) = GCD(-6, 12) = GCD(-6, -12) = GCD(6, 12) = 6.

Q3: Do any two positive integers always have a GCD?

Ans: Yes, as it’s the largest factor dividing both numbers.