Hamiltonian Path Problem

Problem Statement:

Given an undirected graph. The task is to print all the Hamiltonian cycles present in the graph.

A Hamiltonian Cycle is a cycle that traverses all the nodes of the graph exactly once and returns back to the starting point.

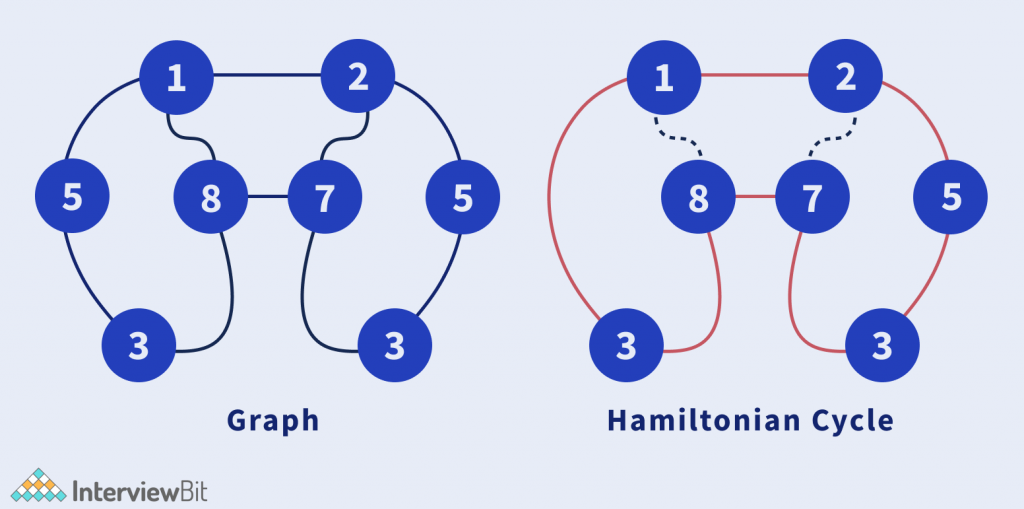
Example :

Input :

Approach: Backtracking

The problem can be solved using a backtracking approach. Follow the below steps to solve the problem.

Algorithm:

• Create an empty path array.
• Add the vertex 0 to the array.
• Start adding vertex 1 and other connected nodes and check if the current vertex can be included in the array or not.
• This can be done by using a visiting array and checking if the vertex has already been visited or is adjacent to the previously added vertex.
• If any such vertex is found, add it to the array and backtrack from that node.
• Try every possible combination and if a path returns false, ignore the vertex and start iterating from the next vertex till all the nodes have been visited.

Implementation of the Approach:

C++ Code

#define N 8
//vertices
char vertices[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'};
//adjacency matrix
int adjacencyM[N][N]= {{0, 1, 0, 0, 0, 0, 0, 1},
                       {1, 0, 1, 0, 0, 0, 0, 0},
                       {0, 1, 0, 1, 0, 0, 0, 1},
                       {0, 0, 1, 0, 1, 0, 1, 0},
                       {0, 0, 0, 1, 0, 1, 0, 0},
                       {0, 0, 0, 0, 1, 0, 1, 0},
                       {0, 0, 0, 1, 0, 1, 0, 1},
                       {1, 0, 1, 0, 0, 0, 1, 0}};
 
//list mapping of vertices to mark vertex visited
int visited[N] {
  0
};
 
class Hamiltonian {
  public:
    //start (& end) vertex
    int start;
  //stack used as list to store the path of the cycle
  list < int > cycle;
  //variable to mark if graph has the cycle
  bool hasCycle = false;
//constructor
  Hamiltonian(int start) {
    this -> start = start;
  }
 
  //method to initiate the search of the Hamiltonian cycle
  void findCycle() {
    //add starting vertex to the list
    cycle.push_back(start);
 
    //start searching the path
    solve(start);
  }
 
  void solve(int vertex) {
    //Base condition: if the vertex is the start vertex
    //and all nodes have been visited (start vertex twice)
    if (vertex == start && cycle.size() == N + 1) {
      hasCycle = true;
 
      //output the cycle
      displayCycle();
 
      //return to explore more hamiltonian cycles
      return;
    }
 
    //iterate through the neighbor vertices
    for (int i = 0; i < N; i++) {
      if (adjacencyM[vertex][i] == 1 && visited[i] == 0) {
        int nbr = i;
        //visit and add vertex to the cycle
        visited[nbr] = 1;
        cycle.push_back(nbr);
 
        //Go to the neighbor vertex to find the cycle
        solve(nbr);
   //Backtrack
        visited[nbr] = 0;
        cycle.pop_back();
      }
    }
  }
 
  //Function to display hamiltonian cycle
  void displayCycle() {
    cout << "[";
    for (int v: cycle) {
      cout << vertices[v] << " ";
    }
    cout << "] \n";
  }
};

Java Code

 class Hamiltonian {
  //vertices
  char vertices[];
  //adjacency matrix
  int adjacencyM[][];
  //list mapping of vertices to mark vertex visited
  int visited[];
  //start (& end) vertex index
  int start;
  //stack used as list to store the path of the cycle
  Stack < Integer > cycle = new Stack < > ();
  //number of vertices in the graph
  int N;
  //variable to mark if graph has the cycle
  boolean hasCycle = false;
 
  //constructor
  Hamiltonian(int start, char vertices[], int adjacencyM[][]) {
    this.start = start;
    this.vertices = vertices;
    this.adjacencyM = adjacencyM;
    this.N = vertices.length;
    this.visited = new int[vertices.length];
  }
 
  //method to initiate the search of the Hamiltonian cycle
  public void findCycle() {
    //add starting vertex to the list
    cycle.push(start);
 
    //start searching the path
    solve(start);
  }
 
  private void solve(int vertex) {
    //Base condition: if the vertex is the start vertex
    //and all nodes have been visited (start vertex twice)
    if (vertex == start && cycle.size() == N + 1) {
      hasCycle = true;
 
      //output the cycle
      displayCycle();
 
      //return to explore more hamiltonian cycles
      return;
    }
 
    //iterate through the neighbor vertices
    for (int i = 0; i < N; i++) {
      if (adjacencyM[vertex][i] == 1 && visited[i] == 0) {
        int nbr = i;
        //visit and add vertex to the cycle
        visited[nbr] = 1;
        cycle.push(nbr);
 
        //Go to the neighbor vertex to find the cycle
        solve(nbr);
 
        //Backtrack
        visited[nbr] = 0;
    cycle.pop();
      }
    }
  }
 
  //Method to display the path of the cycle
  void displayCycle() {
    //converting vertex index to the name
    List < Character > names = new ArrayList < > ();
    for (int idx: cycle) {
      names.add(vertices[idx]);
    }
    System.out.println(names);
  }
}
class Main {
  public static void main(String[] args) {
    //vertices
    char vertices[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'};
    //adjacency matrix
    int adjacencyM[][]= {{0, 1, 0, 0, 0, 0, 0, 1},
                         {1, 0, 1, 0, 0, 0, 0, 0},
                         {0, 1, 0, 1, 0, 0, 0, 1},
                         {0, 0, 1, 0, 1, 0, 1, 0},
                         {0, 0, 0, 1, 0, 1, 0, 0},
                         {0, 0, 0, 0, 1, 0, 1, 0},
                         {0, 0, 0, 1, 0, 1, 0, 1},
                         {1, 0, 1, 0, 0, 0, 1, 0}};
 
    //Driver code
    Hamiltonian hamiltonian = new Hamiltonian(0,vertices, adjacencyM);
    hamiltonian.findCycle();
 
    //if the graph doesn't have any Hamiltonian Cycle
    if(!hamiltonian.hasCycle){
      System.out.println("No Hamiltonian Cycle");
    }
  }
}

Python Code

class Hamiltonian:
    def __init__(self, start):
        # start (& end) vertex
        self.start = start
 
        # list to store the cycle path
        self.cycle = []
 
        # variable to mark if graph has the cycle
        self.hasCycle = False
 
    # method to initiate the search of cycle
    def findCycle(self):
        # add starting vertex to the list
        self.cycle.append(self.start)
 
        # start the search of the hamiltonian cycle
        self.solve(self.start)
 
    # recursive function to implement backtracking
    def solve(self, vertex):
        # Base condition: if the vertex is the start vertex
        # and all nodes have been visited (start vertex twice)
        if vertex == self.start and len(self.cycle) == N + 1:
            self.hasCycle = True
 
            # output the cycle
            self.displayCycle()
 
            # return to explore more cycles
            return
 
        # iterate through the neighbor vertices
        for i in range(len(vertices)):
            if adjacencyM[vertex][i] == 1 and visited[i] == 0:
                nbr = i
 # visit and add vertex to the cycle
                visited[nbr] = 1
                self.cycle.append(nbr)
 
                # traverse the neighbor vertex to find the cycle
                self.solve(nbr)
 
                # Backtrack
                visited[nbr] = 0
                self.cycle.pop()
 
    # function to display the hamiltonian class
    def displayCycle(self):
        names = []
        for v in self.cycle:
            names.append(vertices[v])
        print(names)
 
if __name__ == '__main__':
  vertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
  adjacencyM = [[0, 1, 0, 0, 0, 0, 0, 1],
                [1, 0, 1, 0, 0, 0, 0, 0],
                [0, 1, 0, 1, 0, 0, 0, 1],
                [0, 0, 1, 0, 1, 0, 1, 0],
                [0, 0, 0, 1, 0, 1, 0, 0],
                [0, 0, 0, 0, 1, 0, 1, 0],
                [0, 0, 0, 1, 0, 1, 0, 1],
                [1, 0, 1, 0, 0, 0, 1, 0]]
  #list mapping of vertices to mark vertex visited
  visited = [0 for x in range(len(vertices))]
 
  #number of vertices in the graph
  N = 8
 
  #Driver code
  hamiltonian = Hamiltonian(0)
  hamiltonian.findCycle()
 
  #if the graph doesn't have any Hamiltonian Cycle
  if not hamiltonian.hasCycle:
 print("No Hamiltonian Cycle")

• Time Complexity: O(N!), where N is the number of vertices.
• Space Complexity: O(1), as no extra space is used.

Practice Questions:

• Cycle in Undirected Graph

FAQ

Q.1: What is the time and space complexity of the backtracking approach?

Ans: The time and space complexity of the backtracking approach. is O(N!) and O(1), where N is the number of vertices.

Q.2: What is a Hamiltonian Cycle?

Ans: A Hamiltonian Cycle is a cycle that traverses all the nodes of the graph exactly once and returns back to the starting point.