Josephus Problem

Problem Statement

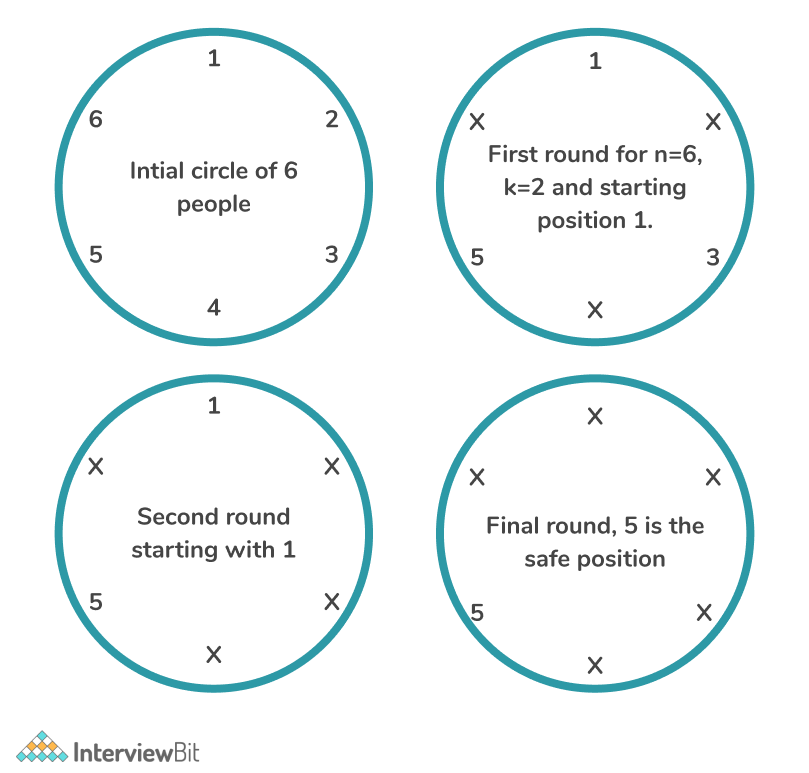
There are N people standing in a circle numbered from 1 to N. Also given an integer K. First, count the K-th number starting from the first one and delete it. Then K numbers are counted starting from the next one and the K-th one is removed again, and so on. The process stops when one number remains. The task is to find the last number.

Examples:

• Input: N = 6, K = 2
• Output: 5

Explanation:

Recursive Approach

A simple approach to solve this problem is to find the position of the step which would be called after each execution.

Therefore, given N persons, and skipping K persons during their deletion, N – 1 persons will be left. Therefore, we need to call the recursive function for N – 1 and K for the next iteration.

Now, for each remaining circle after execution, we need to find the last remaining person present i.e. if Kth person is executed, K+1th will be the next starting safe point the recursive call. Therefore, to keep a track of the position, perform K%N + 1.

The recursive function would be:

josephus(N, K) = (josephus(N – 1 , K) + K – 1) % N + 1.

You can also observe a pattern as follows:

Algorithm

• If N  == 1, return 1. This is the termination condition for the function.
• Else, return (josephus(N – 1 , K) + K – 1) % N + 1.

C++ Code

int josephus(int N, int K) {
  if (N == 1)
    return 1;
  else
    return (josephus(N - 1, K) + K - 1) % N + 1;
}

Java Code

 static int josephus(int N, int K) {
  if (N == 1)
    return 1;
  else
    return (josephus(N - 1, K) + K - 1) % N + 1;
}

Python Code

def josephus(N, K):
 
    if N == 1:
        return 1
    else:
        return (josephus(N - 1, K) + K - 1) % N + 1

• Time Complexity: O(N)
• Space Complexity: O(N), depth of the recursion tree.

Using List – Approach 2

In this approach, initialize a list containing all integers from 1 to N and delete every Kth node until one element is left.

Algorithm

• Create a list containing integers from 1 to N.
• Create a recursive function which deletes every Kth element from the list in each iteration in the clockwise direction.
• Continue repeating the above steps until only one element is left.

Implementation of the Approach:

C++ Code

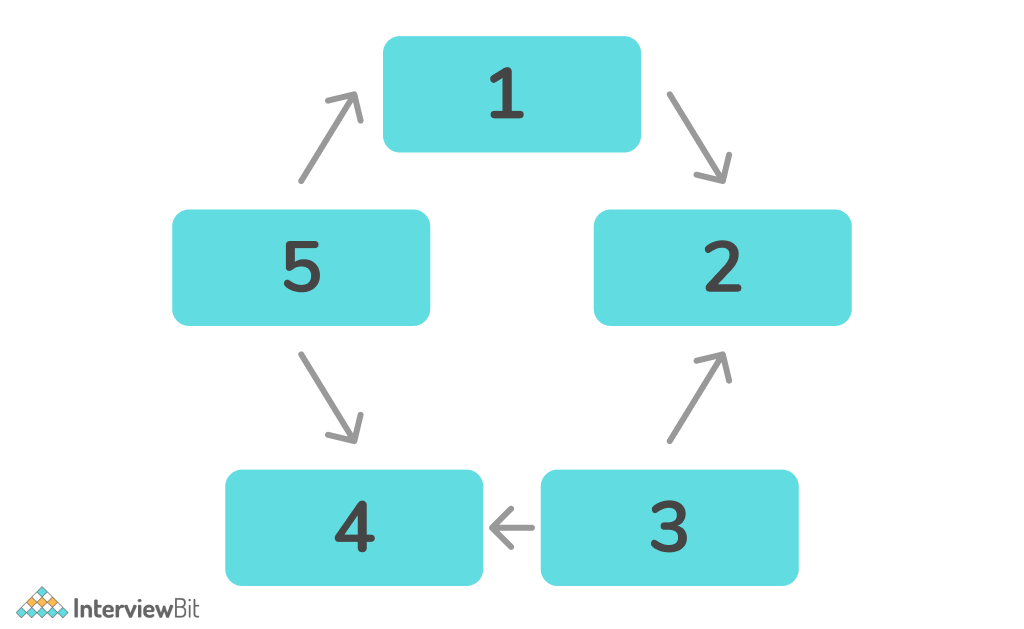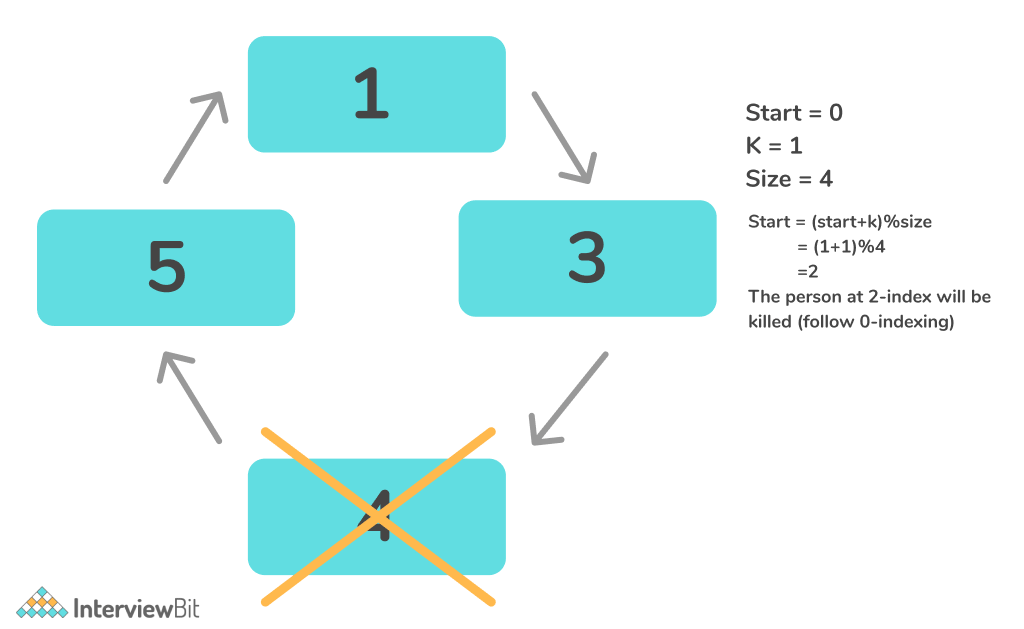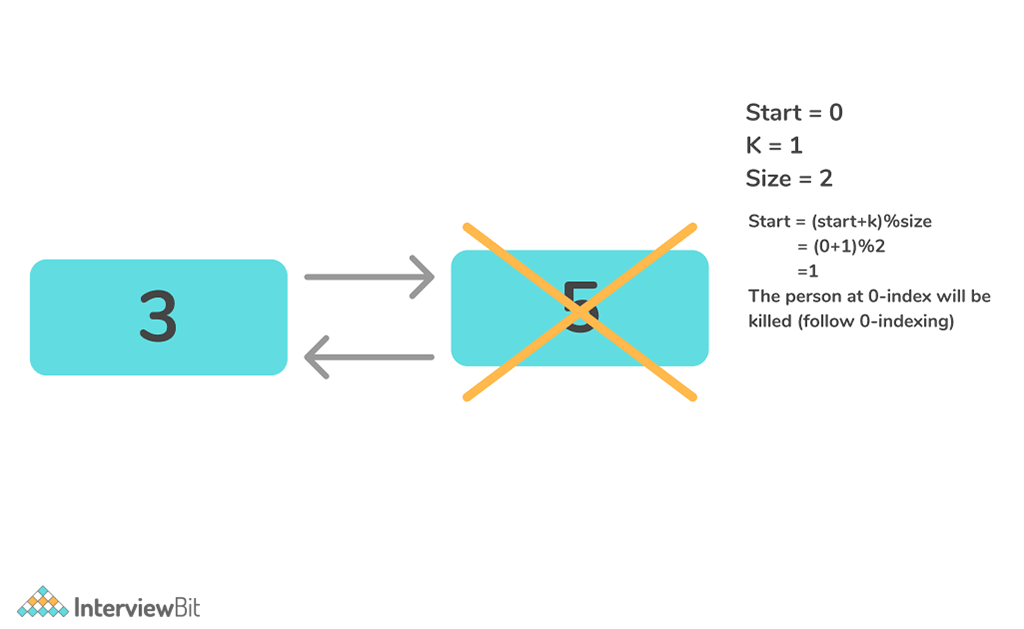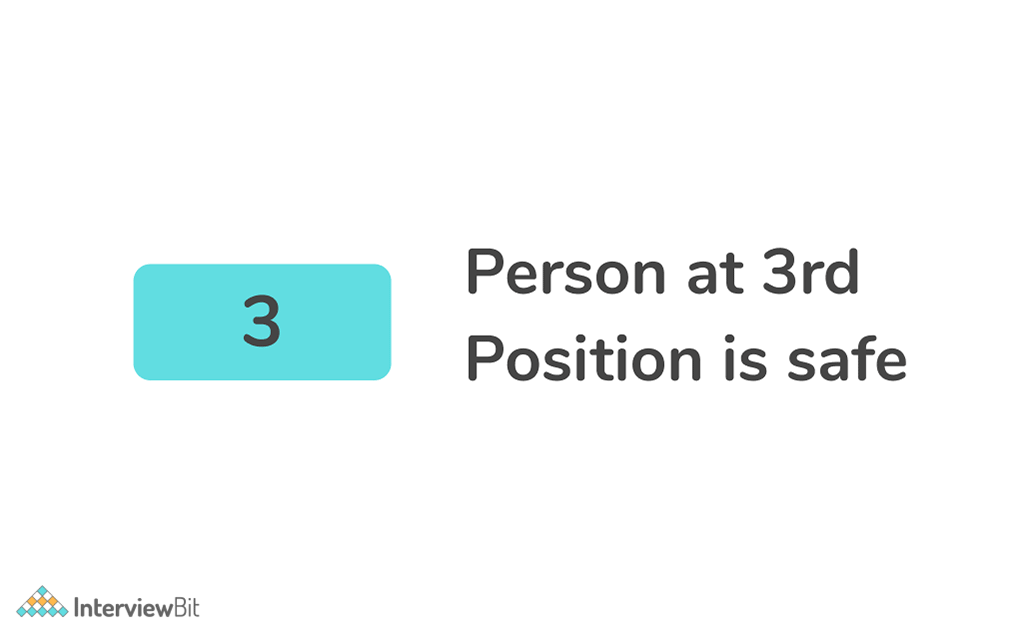
void Josh(vector < int > person, int k, int index) {
  if (person.size() == 1) {
    cout << person[0] << endl;
    return;
  }
  index = ((index + k) % person.size());
  person.erase(person.begin() + index);
  Josh(person, k, index);
}
 
solve(n, k) {
  k--;
  int index = 0;
 
  vector < int > person;
  for (int i = 1; i <= n; i++) {
    person.push_back(i);
  }
 
  Josh(person, k, index);
}

Java Code

 static void Josh(ArrayList < Integer > person, int k, int index) {
  if (person.size == 1) {
    System.out.println(person.get(0));
    return;
  }
  index = ((index + k) % person.size());
  person.remove(index);
  Josh(person, k, index);
}
 
solve(int N, int K) {
  K = K - 1;
  int index = 0;
 
  Arraylist < Integer > person;
  for (int i = 1; i <= N; i++) {
    person.push_back(i);
  }
 
  Josh(person, K, index);
}

Python Code

def Josh(person, k, index):
    if len(person) == 1:
        print(person[0])
        return
 
    index = (index + k) % len(person)
    person.pop(index)
    Josh(person, k, index)
 
 
def solve(N, K):
 
    K = K - 1
    index = 0
 
    persons = [0] * (N)
    for i in range(1, N + 1):
        person.append(i)
 
    Josh(person, K, index)

• Time Complexity: O(N), where N is total persons.
• Space Complexity: O(N), a list of size N, is used.

Special Case: K = 2

For K = 2, the problem becomes much easier to solve.

In case, N is even, first all even positions will get deleted. Then, the remaining N / 2 remains. Therefore, the answer for the remaining N can be found from the answer for N / 2 by multiplying it with 2 and subtracting 1 i.e. shifting the positions.

The answer for even N can obtained as –

josephus(2 * N, 2) =  josephus(N, 2) – 1

Similarly, In case, N is odd, first, all even positions will get deleted. Then, remaining (N – 1) / 2 remains. Therefore, the answer for the remaining N can be found from the answer for (N – 1) / 2 by multiplying it with 2 and subtracting 1 i.e. shifting the positions.

The answer for even N can obtained as –

josephus(2 * N + 1, 2) =  josephus(N, 2) – 1

From the above relations, both can be merged and can be written as –

josephus(N, 2) = 1 + 2 * (N – 2 ^(floor(log2(N))

C++ Code

int josephus(int N) {
  int p = 1;
  while (p <= N)
    p *= 2;
 
  return (2 * N) - p + 1;
}

Java Code

 static int josephus(int N) {
  int p = 1;
  while (p <= N)
    p *= 2;
 
  return (2 * N) - p + 1;
}

Python Code

def josephus(N):
    p = 1
    while p <= N:
        p *= 2
 
    return (2 * N) - p + 1

• Time Complexity: O(logN), where N is the total steps.
• Space Complexity: O(1), as no extra s[ace is used.

Practice Question

• 100 People In A Circle

FAQs

Q.1: What data structure is used in solving the Josephus problem?

Ans: A list can be used to solve the Josephus problem, which initially contains all the integers from 1 to N.

Q.2: How to solve the Josephus problem?

Ans: The Josephus problem can be solved using recursion. For each iteration, recursively delete the Kth position until only one person is left.