Problem Statement
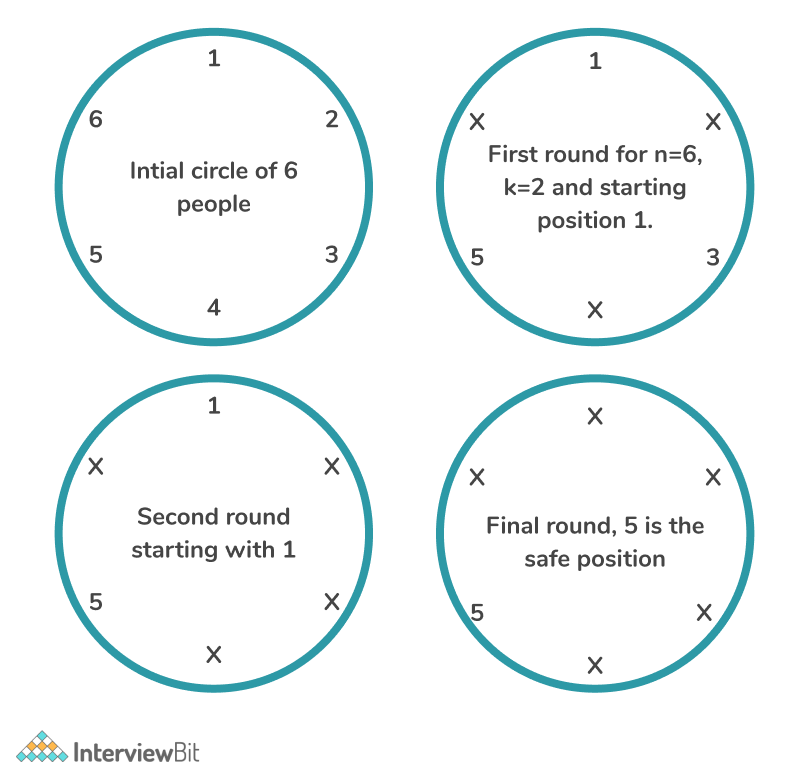
There are N people standing in a circle numbered from 1 to N. Also given an integer K. First, count the K-th number starting from the first one and delete it. Then K numbers are counted starting from the next one and the K-th one is removed again, and so on. The process stops when one number remains. The task is to find the last number.

Examples:
- Input: N = 6, K = 2
- Output: 5
Explanation:
Confused about your next job?
Recursive Approach
A simple approach to solve this problem is to find the position of the step which would be called after each execution.
Therefore, given N persons, and skipping K persons during their deletion, N – 1 persons will be left. Therefore, we need to call the recursive function for N – 1 and K for the next iteration.
Now, for each remaining circle after execution, we need to find the last remaining person present i.e. if Kth person is executed, K+1th will be the next starting safe point the recursive call. Therefore, to keep a track of the position, perform K%N + 1.
The recursive function would be:
josephus(N, K) = (josephus(N – 1 , K) + K – 1) % N + 1.
You can also observe a pattern as follows:
Algorithm
- If N == 1, return 1. This is the termination condition for the function.
- Else, return (josephus(N – 1 , K) + K – 1) % N + 1.
C++ Code
int josephus(int N, int K) {
if (N == 1)
return 1;
else
return (josephus(N - 1, K) + K - 1) % N + 1;
}Java Code
static int josephus(int N, int K) {
if (N == 1)
return 1;
else
return (josephus(N - 1, K) + K - 1) % N + 1;
}Python Code
def josephus(N, K):
if N == 1:
return 1
else:
return (josephus(N - 1, K) + K - 1) % N + 1- Time Complexity: O(N)
- Space Complexity: O(N), depth of the recursion tree.
Using List – Approach 2
In this approach, initialize a list containing all integers from 1 to N and delete every Kth node until one element is left.
Algorithm
- Create a list containing integers from 1 to N.
- Create a recursive function which deletes every Kth element from the list in each iteration in the clockwise direction.
- Continue repeating the above steps until only one element is left.
Implementation of the Approach:
C++ Code
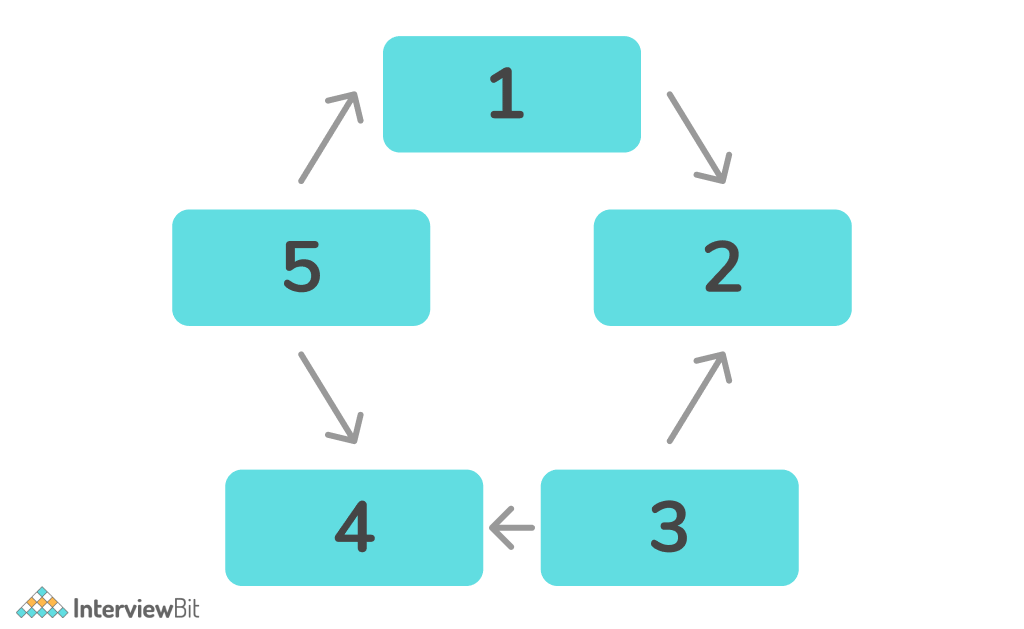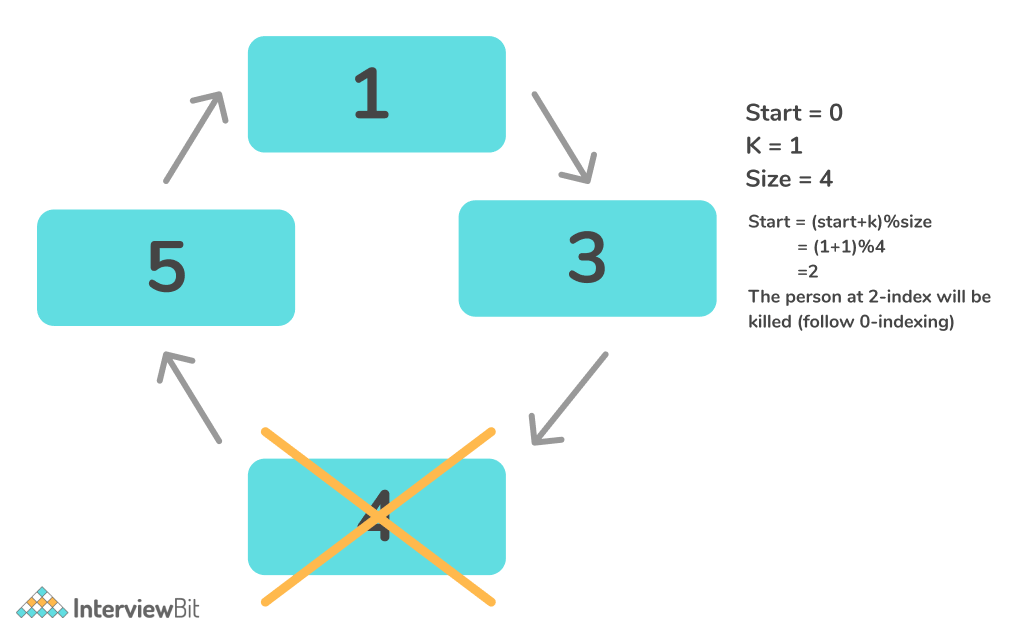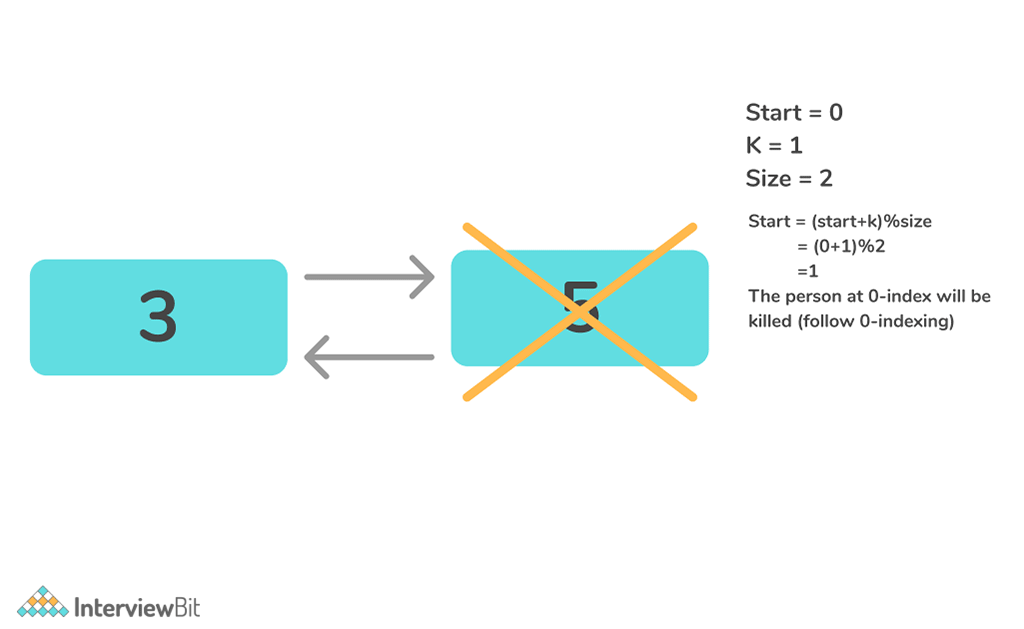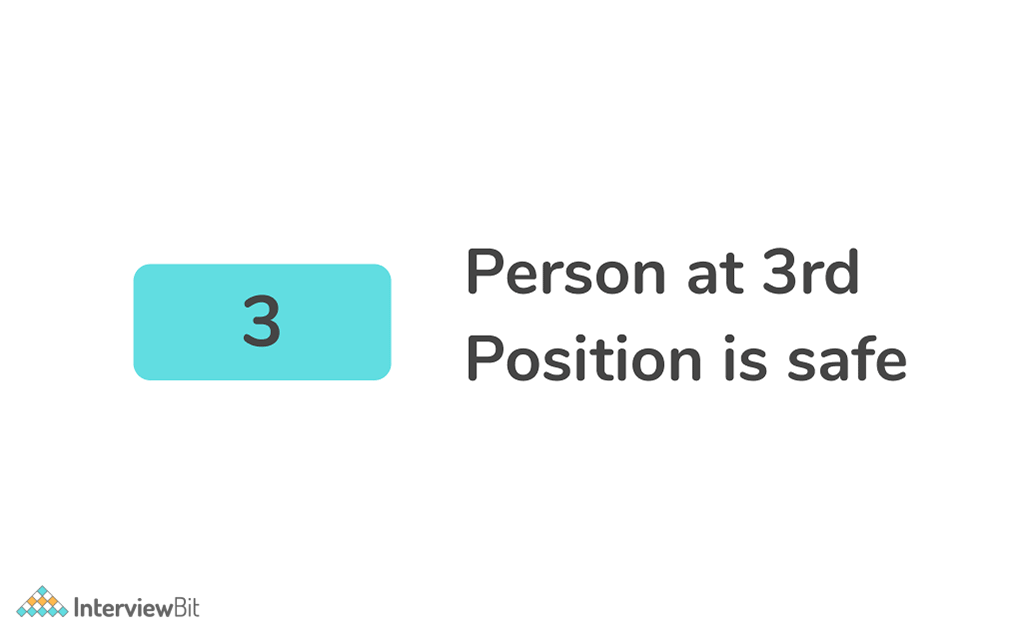
void Josh(vector < int > person, int k, int index) {
if (person.size() == 1) {
cout << person[0] << endl;
return;
}
index = ((index + k) % person.size());
person.erase(person.begin() + index);
Josh(person, k, index);
}
solve(n, k) {
k--;
int index = 0;
vector < int > person;
for (int i = 1; i <= n; i++) {
person.push_back(i);
}
Josh(person, k, index);
}Java Code
static void Josh(ArrayList < Integer > person, int k, int index) {
if (person.size == 1) {
System.out.println(person.get(0));
return;
}
index = ((index + k) % person.size());
person.remove(index);
Josh(person, k, index);
}
solve(int N, int K) {
K = K - 1;
int index = 0;
Arraylist < Integer > person;
for (int i = 1; i <= N; i++) {
person.push_back(i);
}
Josh(person, K, index);
}Python Code
def Josh(person, k, index):
if len(person) == 1:
print(person[0])
return
index = (index + k) % len(person)
person.pop(index)
Josh(person, k, index)
def solve(N, K):
K = K - 1
index = 0
persons = [0] * (N)
for i in range(1, N + 1):
person.append(i)
Josh(person, K, index)- Time Complexity: O(N), where N is total persons.
- Space Complexity: O(N), a list of size N, is used.
Special Case: K = 2
For K = 2, the problem becomes much easier to solve.
In case, N is even, first all even positions will get deleted. Then, the remaining N / 2 remains. Therefore, the answer for the remaining N can be found from the answer for N / 2 by multiplying it with 2 and subtracting 1 i.e. shifting the positions.
The answer for even N can obtained as –
josephus(2 * N, 2) = josephus(N, 2) – 1
Similarly, In case, N is odd, first, all even positions will get deleted. Then, remaining (N – 1) / 2 remains. Therefore, the answer for the remaining N can be found from the answer for (N – 1) / 2 by multiplying it with 2 and subtracting 1 i.e. shifting the positions.
The answer for even N can obtained as –
josephus(2 * N + 1, 2) = josephus(N, 2) – 1
From the above relations, both can be merged and can be written as –
josephus(N, 2) = 1 + 2 * (N – 2 ^(floor(log2(N))
C++ Code
int josephus(int N) {
int p = 1;
while (p <= N)
p *= 2;
return (2 * N) - p + 1;
}Java Code
static int josephus(int N) {
int p = 1;
while (p <= N)
p *= 2;
return (2 * N) - p + 1;
}Python Code
def josephus(N):
p = 1
while p <= N:
p *= 2
return (2 * N) - p + 1- Time Complexity: O(logN), where N is the total steps.
- Space Complexity: O(1), as no extra s[ace is used.
Practice Question
FAQs
Q.1: What data structure is used in solving the Josephus problem?
Ans: A list can be used to solve the Josephus problem, which initially contains all the integers from 1 to N.
Q.2: How to solve the Josephus problem?
Ans: The Josephus problem can be solved using recursion. For each iteration, recursively delete the Kth position until only one person is left.




