Largest Rectangle in Histogram

Given an array of integers A[], where each element A[i] represents the height of a bar in histogram. The width of each bar is 1. The task is to return the area of the largest histogram.

Examples:

Input:

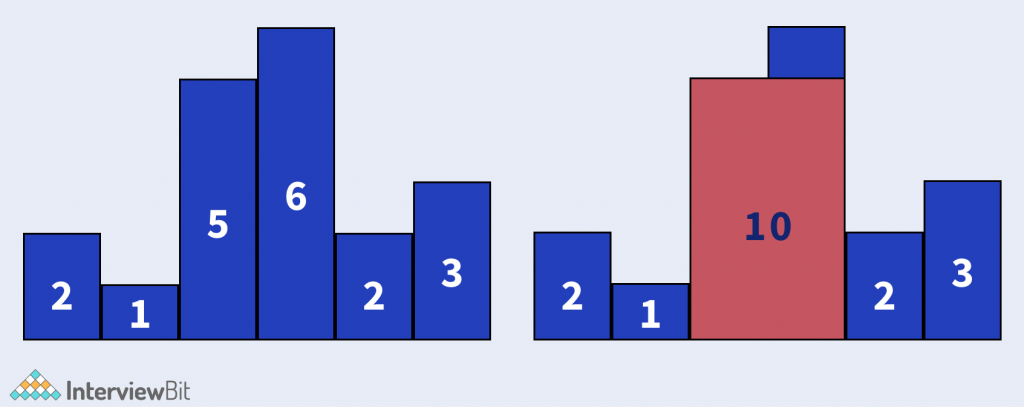
Output: 10
Explanation: Shown in image
Input: 

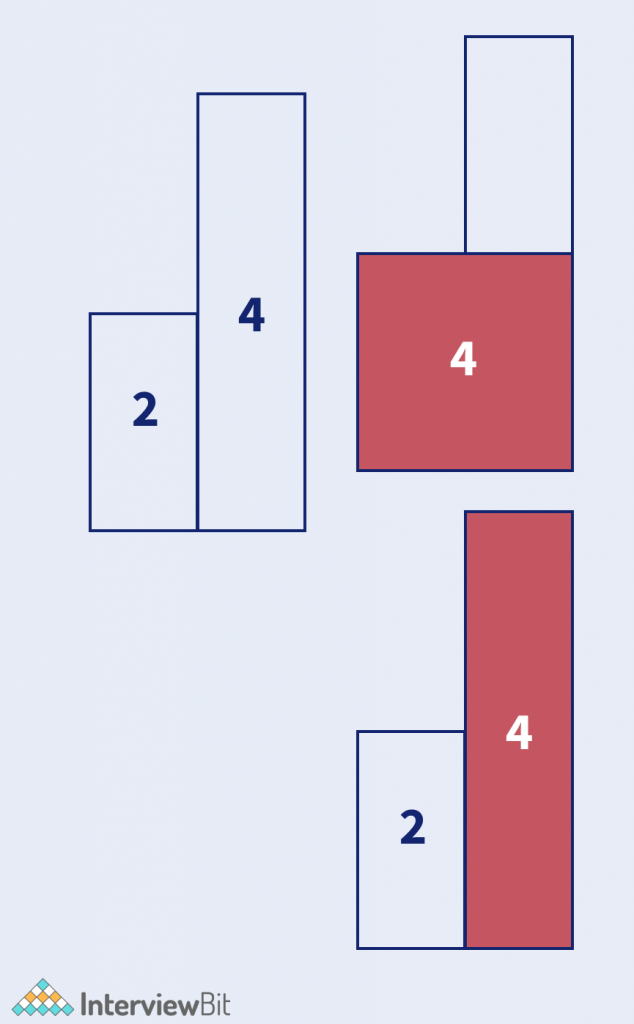
Output: 4
Explanation: Shown in image

Approach 1: Brute Force

The key idea to observe is that the height of the maximum area of the histogram formed between any two bars will always be bounded by the height of the shortest bar lying between them. Observe the below image.

Algorithm:

• Initialise a variable, maxArea = 0, denoting the maximum area of the histogram to be found.
• Run two nested loops from i = 0 till i = N and from j = i till j = N.
• For each jth iteration, run a loop k = i till k = j and find the height of the minimum bar among them.
• The area of the histogram would be minHeight * (j – i + 1).
• Maximize maxArea.

Implementation of the Approach:

C++ Code

int largestRectangleArea(vector < int > & heights) {
  int max_area = 0;
  for (size_t i = 0; i < heights.size(); i++) {
    for (size_t j = i; j < heights.size(); j++) {
      int min_height = INT_MAX;
      for (size_t k = i; k <= j; k++) {
        min_height = min(min_height, heights[k]);
      }
      max_area = max(max_area, min_height * (j - i + 1));
    }
  }
  return max_area;
}

Java Code

 public int largestRectangleArea(int[] heights) {
  int maxarea = 0;
  for (int i = 0; i < heights.length; i++) {
    for (int j = i; j < heights.length; j++) {
      int minheight = Integer.MAX_VALUE;
      for (int k = i; k <= j; k++)
        minheight = Math.min(minheight, heights[k]);
      maxarea = Math.max(maxarea, minheight * (j - i + 1));
    }
  }
  return maxarea;
}

Python Code

def largestRectangleArea(heights):
    max_area = 0
    for i in range(len(heights)):
        for j in range(i, len(heights)):
            min_height = inf
            for k in range(i, j + 1):
                min_height = min(min_height, heights[k])
            max_area = max(max_area, min_height * (j - i + 1))
    return max_area

Time Complexity: O(N^3), where N is the size of the array

Space Complexity: O(1), as no extra space is used.

Approach 2: Divide and Conquer

Instead of traversing through all the elements from A[i] and A[j] again, the idea is to use divide and conquer algorithm.

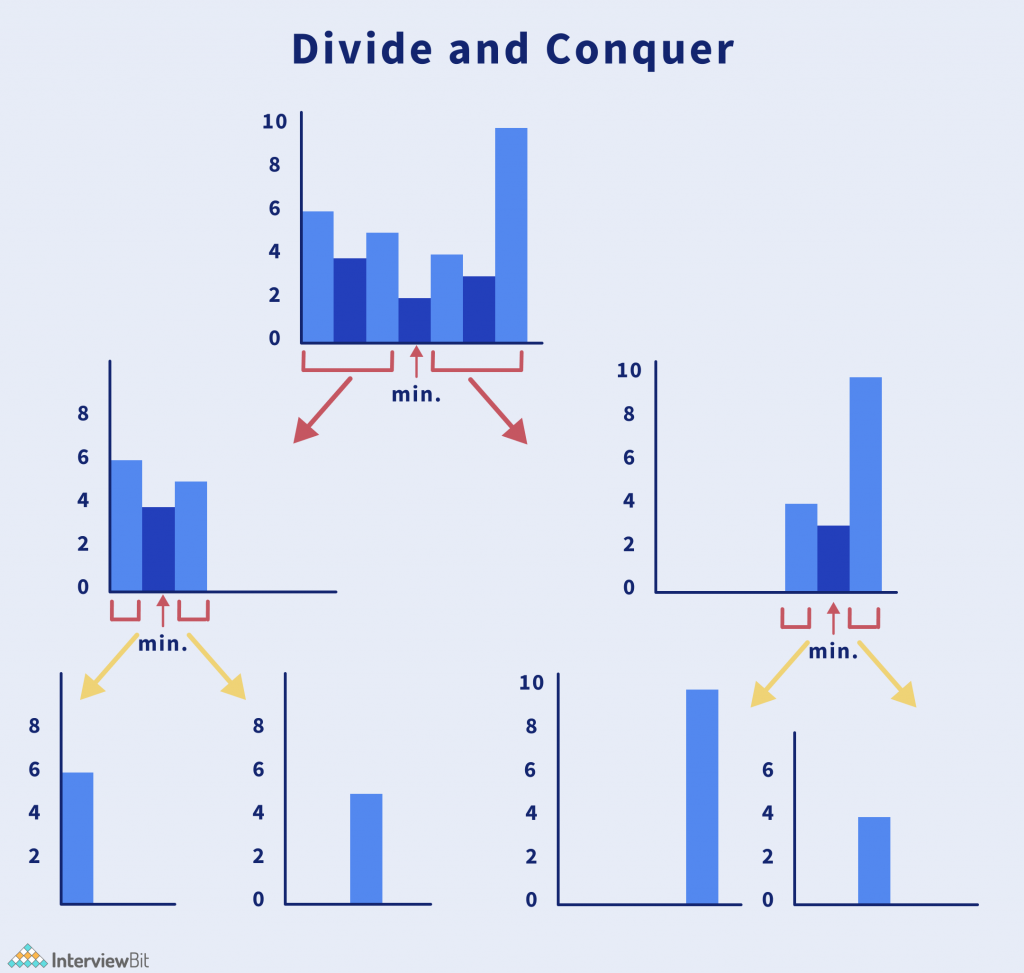
Let us think, how can we obtain the rectangle with maximum area in the histogram.
If you observe clearly, it is based upon these three ideas:

• The rectangle with the widest possible width and height equal to the shortest bar.
• The area of the rectangle formed on the left side of the minimum height.
• The area of the rectangle formed on the right side of the minimum height.

Implementation of the Approach:

C++ Code

int calculateArea(vector < int > & heights, int start, int end) {
  if (start > end) {
    return 0;
  }
  int min_index = start;
  for (int i = start; i <= end; i++) {
    if (heights[min_index] > heights[i]) {
      min_index = i;
    }
  }
  return max({
    heights[min_index] * (end - start + 1),
    calculateArea(heights, start, min_index - 1),
    calculateArea(heights, min_index + 1, end)
  });
}
 
int largestRectangleArea(vector < int > & heights) {
  return calculateArea(heights, 0, heights.size() - 1);
}

Java Code

public int calculateArea(int[] heights, int start, int end) {
  if (start > end)
    return 0;
  int minindex = start;
  for (int i = start; i <= end; i++)
    if (heights[minindex] > heights[i])
      minindex = i;
  return Math.max(heights[minindex] * (end - start + 1),
    Math.max(calculateArea(heights, start, minindex - 1),
      calculateArea(heights, minindex + 1, end))
  );
}
 
public int largestRectangleArea(int[] heights) {
  return calculateArea(heights, 0, heights.length - 1);
}

Python Code

def largestRectangleArea(heights) -> int:
    def calculateArea(heights: List[int], start: int, end: int) -> int:
        if start > end:
            return 0
        min_index = start
        for i in range(start, end + 1):
            if heights[min_index] > heights[i]:
                min_index = i
        return max(
            heights[min_index] * (end - start + 1),
            calculateArea(heights, start, min_index - 1),
            calculateArea(heights, min_index + 1, end),
        )
 
    return calculateArea(heights, 0, len(heights) - 1)

Time Complexity: O(NlogN), where N is the size of the array

Space Complexity: O(N), since array is used.

Approach 3: Stack

The idea is similar to finding the Next Greater element using stack. In this problem, instead of finding the next greater element, we will maintain two arrays left[] and right[] denoting the smaller elements on the left and right. Look at the animation below for better understanding:

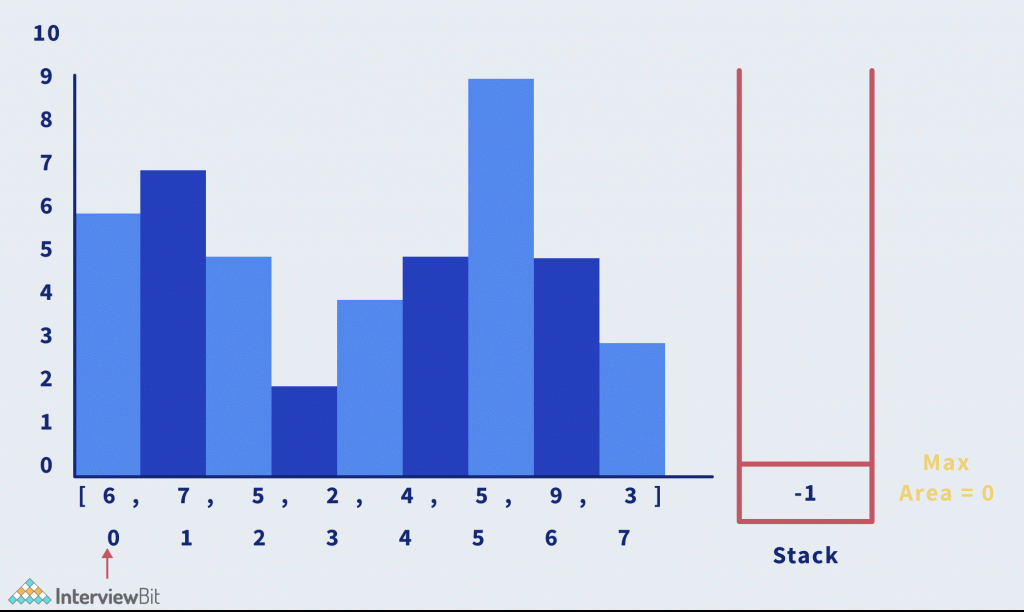
Algorithm:

• Initialise a stack S.
• Push the first index of A[] into the stack.
• Traverse through the array A[] and compare the height of A[i] with the height at the top of the stack.
• If the height is:
  • Greater than A[S.top()], push it into the stack.
  • Less than A[S.top()], keep popping the elements until A[i] >= A[S.top()].
• Keep maximizing the area while popping the elements from the stack.
• Push the index i for each element.
• Return the maximum element.

Implementation of the Approach:

C++ Code

int largestRectangleArea(vector < int > & heights) {
  stack < int > stk;
  stk.push(-1);
  int max_area = 0;
  for (size_t i = 0; i < heights.size(); i++) {
    while (stk.top() != -1 and heights[stk.top()] >= heights[i]) {
      int current_height = heights[stk.top()];
      stk.pop();
      int current_width = i - stk.top() - 1;
      max_area = max(max_area, current_height * current_width);
    }
    stk.push(i);
  }
  while (stk.top() != -1) {
    int current_height = heights[stk.top()];
    stk.pop();
    int current_width = heights.size() - stk.top() - 1;
    max_area = max(max_area, current_height * current_width);
  }
  return max_area;
}

Java Code

 public int largestRectangleArea(int[] heights) {
   Deque < Integer > stack = new ArrayDeque < > ();
   stack.push(-1);
   int length = heights.length;
   int maxArea = 0;
   for (int i = 0; i < length; i++) {
     while ((stack.peek() != -1) &&
       (heights[stack.peek()] >= heights[i])) {
       int currentHeight = heights[stack.pop()];
       int currentWidth = i - stack.peek() - 1;
       maxArea = Math.max(maxArea, currentHeight * currentWidth);
     }
     stack.push(i);
   }
   while (stack.peek() != -1) {
     int currentHeight = heights[stack.pop()];
     int currentWidth = length - stack.peek() - 1;
     maxArea = Math.max(maxArea, currentHeight * currentWidth);
   }
   return maxArea;
 }

Python Code

def largestRectangleArea(self, heights):
    stack = [-1]
    max_area = 0
    for i in range(len(heights)):
        while stack[-1] != -1 and heights[stack[-1]] >= heights[i]:
            current_height = heights[stack.pop()]
            current_width = i - stack[-1] - 1
            max_area = max(max_area, current_height * current_width)
        stack.append(i)
 
    while stack[-1] != -1:
        current_height = heights[stack.pop()]
        current_width = len(heights) - stack[-1] - 1
        max_area = max(max_area, current_height * current_width)
    return max_area

Time Complexity: O(N), where N is the size of the array

Space Complexity: O(N), since stack is used.

Practice Questions:

Largest Rectangle in Histogram

FAQ

• Can the brute force approach be improved?
  Yes, we can run two nested loops and find the minimum height on both left and right half while iterating and maximizing the area. The time complexity would be O(N^2).