Given a string s and a dictionary of strings. The task is to check whether the given string S can be broken into individual words from the dictionary.
Examples:
Input:
s = “applepenapple”
words = [“apple”, “pen”];
Confused about your next job?
Output: True
Explanation:
The string “applepenapple” can be broken into “apple pen apple”
Input:
s = “catsandog”
words = [“cats”, “dog”, “sand”, “and”, “cat”]
Output: False
Approach 1: Brute Force
The most basic approach to solve this problem is to simply use recursion and backtracking. The key idea is to check every possible prefix of the given string in the dictionary of words. If the prefix is found in the dictionary of words, run the recursive function for the rest of the string and at any point if the whole string is found, simply return True.
Implementation of the Approach:
C++ Code
bool wordBreak(string s, vector < string > & wordDict) {
set < string > word_set(wordDict.begin(), wordDict.end());
return wordBreakRecur(s, word_set, 0);
}
bool wordBreakRecur(string & s, set < string > & word_set, int start) {
if (start == s.length()) {
return true;
}
for (int end = start + 1; end <= s.length(); end++) {
if (word_set.find(s.substr(start, end - start)) != word_set.end() and wordBreakRecur(s, word_set, end)) {
return true;
}
}
return false;
}Java Code
public boolean wordBreak(String s, List < String > wordDict) {
return wordBreakRecur(s, new HashSet < > (wordDict), 0);
}
private boolean wordBreakRecur(String s, Set < String > wordDict, int start) {
if (start == s.length()) {
return true;
}
for (int end = start + 1; end <= s.length(); end++) {
if (wordDict.contains(s.substring(start, end)) && wordBreakRecur(s, wordDict, end)) {
return true;
}
}
return false;
}Python Code
def wordBreak(self, s, wordDict: List[str]) -> bool:
def wordBreakRecur(s: str, word_dict: Set[str], start: int):
if start == len(s):
return True
for end in range(start + 1, len(s) + 1):
if s[start:end] in word_dict and wordBreakRecur(s, word_dict, end):
return True
return False
return wordBreakRecur(s, set(wordDict), 0)Time Complexity: O(2^N), where N is the length of the string S.
Space Complexity: O(N), for the recursive stack.
Approach 2: Dynamic Programming
In the previous approach, if you observe carefully, there were many overlapping subproblems which we were calculating again and again.
For example :
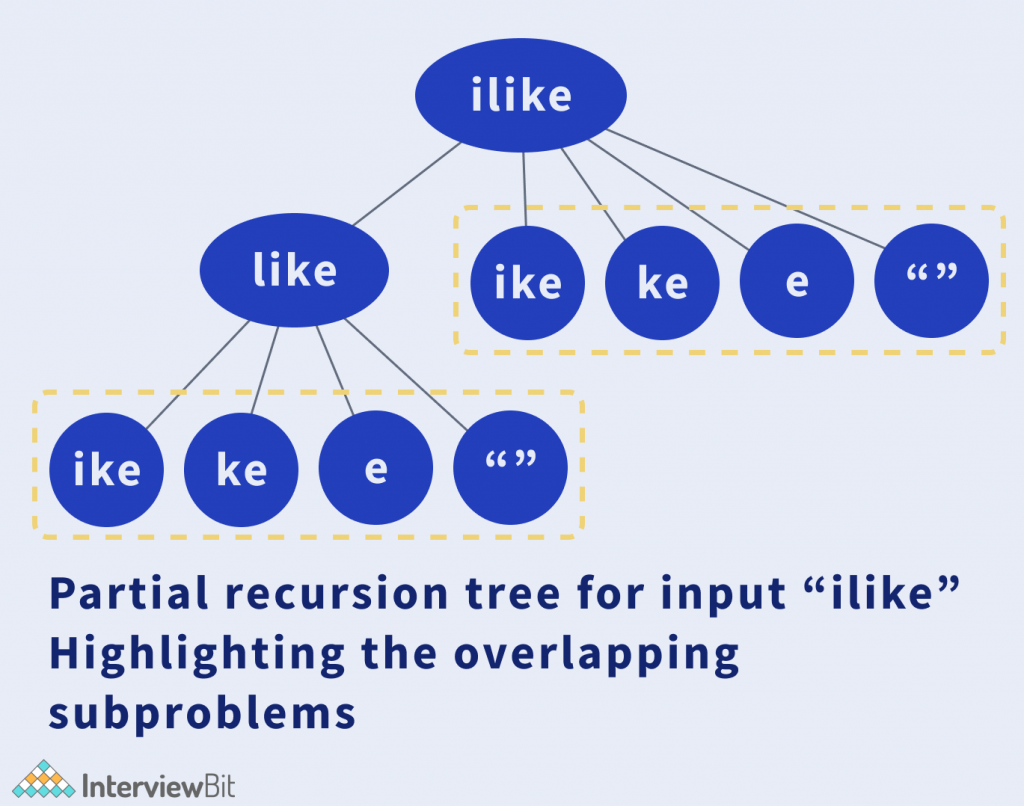
To avoid repetitive calculations, the idea is to use Dynamic Programming to solve the problem.
The intuition behind this approach is that the given problem (s) can be divided into subproblems s1 and s2. If these subproblems individually satisfy the required conditions, the complete problem, s also satisfies the same. e.g. “catsanddog” can be split into two substrings “catsand”, “dog”. The subproblem “catsand” can be further divided into “cats”,”and”, which individually are a part of the dictionary making “catsand” satisfy the condition. Going further backwards, “catsand”, “dog” also satisfy the required criteria individually leading to the complete string “catsanddog” also to satisfy the criteria.
Algorithm:
- Create a 1D dp array of size N + 1, where N is the size of S.
- Consider two pointers i and j, where i refers the starting of the substring and j represents the ending of the substring.
- Run two nested loop, i = 0 till N + 1 and j = 0 to j = i:
- Check if dp[j] > 0 and the dictionary of words contains the substring, then mark dp[i] = True and break.
- Return dp[N] > 0
Implementation of the Approach:
C++ Code
bool wordBreak(string s, vector < string > & wordDict) {
set < string > word_set(wordDict.begin(), wordDict.end());
vector < bool > dp(s.length() + 1);
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] and word_set.find(s.substr(j, i - j)) != word_set.end()) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}Java Code
public boolean wordBreak(String s, List < String > wordDict) {
Set < String > wordDictSet = new HashSet < > (wordDict);
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}Python Code
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
word_set = set(wordDict)
dp = [False] * (len(s) + 1)
dp[0] = True
for i in range(1, len(s) + 1):
for j in range(i):
if dp[j] and s[j:i] in word_set:
dp[i] = True
break
return dp[len(s)]Time Complexity: O(N^3), where N is the length of the string S
Space Complexity: O(N), since dp array is used.
Practice Questions:
FAQ
- What is the time and space complexity of the dynamic programming approach?
The time and space complexity of the dynamic programming approach is O(N^3) and O(N), where N is the length of the given string. - How can you calculate the number of different possible words that can be constructed from the given string?
Following the dynamic programming approach discussed above, instead of making dp[i] = true, add dp[[j – 1] with dp[i] for j > 0. At the end, return dp[N].