Problem Statement
Given a string S. The task is to find the lexicographically smallest string possible by inserting a given character.
A string a is lexicographically smaller than string b (of the same length) if in the first position where a and b differ, string a has a letter that appears earlier in the alphabet than the corresponding letter in b. For example, “abc” is lexicographically smaller than “bac” because ‘a’ comes before ‘b’ in dictionary order.
Examples:
Confused about your next job?
Input: S = “axc”, ch = ‘b’
Output: abxc
Explanation:
Inserting character b in the second position gives the lexicographically smallest string.
Input: S = “abcd”, ch = ‘e’
Output: abcde
Explanation:
Inserting character e in the last index gives the lexicographically smallest string.
Approach
The approach is to insert the given character just before the position, where the S[i] is lexicographically larger than the character ch.
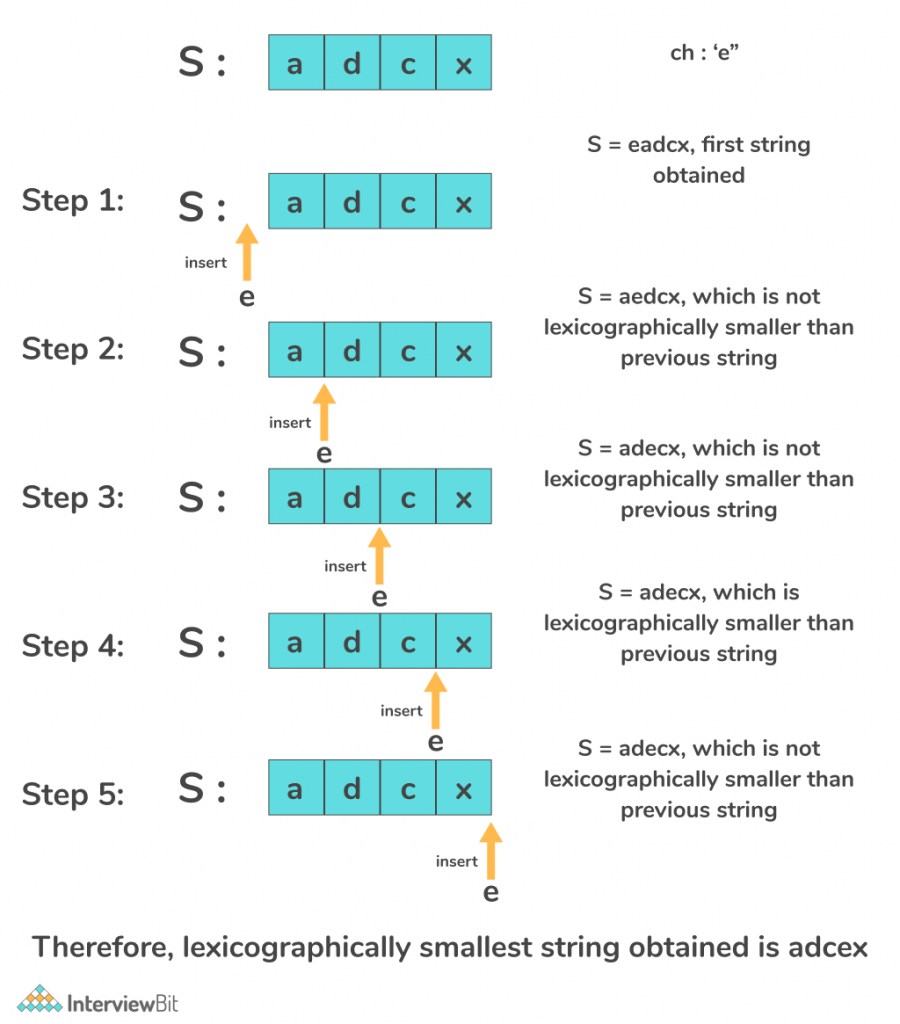
Algorithm:
- Iterate over the string from i = 0 till i = N.
- If the current character of the string S[i] is lexicographically larger than the character ch, insert the character at that index and terminate the loop.
- Else, continue iterating and if no such character is found which is lexicographically greater than ch, insert ch at the end of the string.
C++ Implementation
Java Implementation
Python Implementation
Time Complexity: O(N), where N is the length of the string.
Space Complexity: O(1), as no extra space is used.
Practice Question
Lexicographically Largest Array
Frequently Asked Questions
What is the lexicographically smallest string?
A string a is lexicographically smaller than string b (of the same length) if in the first position where a and b differ, string a has a letter that appears earlier in the alphabet than the corresponding letter in b
What is the time complexity of the insertion of a character at a given position?
The time complexity of insertion of a character at a given position is O(1).




