Longest Common Prefix (With Solution)

Problem Statement

Given the array of strings S[], you need to find the longest string S which is the prefix of ALL the strings in the array.

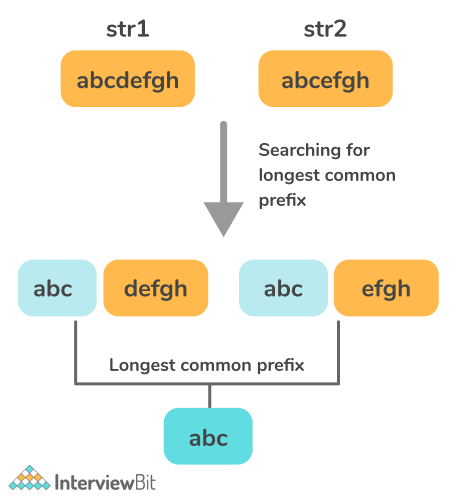
Longest common prefix (LCP) for a pair of strings S1 and S2 is the longest string S which is the prefix of both S1 and S2.

For Example: longest common prefix of “abcdefgh” and “abcefgh” is “ABC”.

Examples:

Input: S[] = {“abcdefgh”, “abcefgh”}
Output: “abc”
Explanation: Explained in the image description above

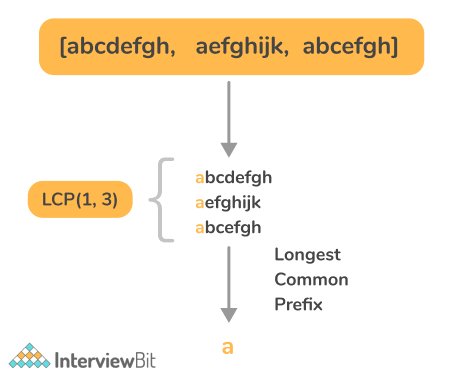
Input: S[] = {“abcdefgh”, “aefghijk”, “abcefgh”}
Output: “a”

Horizontal Scanning Approach

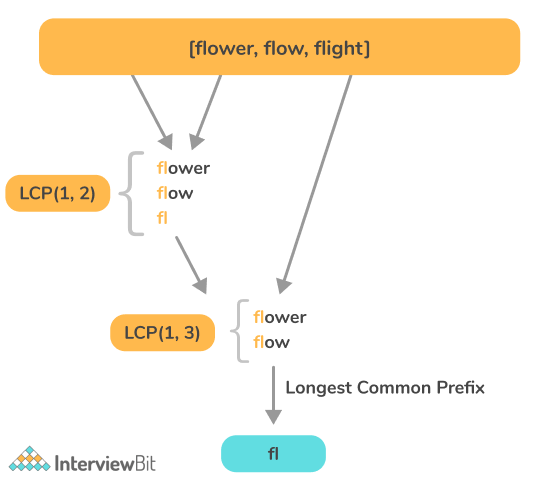
The idea is to horizontally scan all the characters of the array of strings one by one and find the Longest Common Prefix among them. The LCP can be obtained as follows – 

LCP(S1…SN) = LCP(LCP(LCP(S1, S2), S3),…., SN)

Algorithm

• Iterate through the string one by one from S1 till SN.
• For each iteration till ith index, the LCP(S1…Si) can be obtained.
• In case, the LCP is an empty string, terminate loop and return the empty string.
• Else, continue and after scanning of N strings, the LCP(S1…SN) can be obtained.

C++ Implementation Horizontal Scanning

Java Implementation Horizontal Scanning

Python Implementation Horizontal Scanning

Time Complexity: O(N) where N is the size of the array S[].
Space Complexity: O(1), as no extra space is used.

Vertical Scanning Approach

The idea is to scan and compare the characters from top to bottom of the ith index for each string.

This approach is efficient in cases when the LCP string is very small. Hence, we do not need to perform K comparisons.

Algorithm

• Iterate through the string one by one from S1 till SN.
• Start comparing the 0th index, 1st index … ith index simultaneously for each string.
• In case, any of the ith index characters doesn’t match, terminate the algorithm and return the LPS(1,i)
• Else, continue and after scanning of N strings, the LCP(S1…SN) can be obtained.

C++ Implementation of Vertical Scanning

Java Implementation of Vertical Scanning

Python Implementation of Vertical Scanning

Time Complexity: O(K) where K is the sum of all the characters in all strings.
Space Complexity: O(1), as no extra space is used.

Divide and Conquer Approach

The approach is to divide the given array of strings into various subproblems and merge them to get the LCP(S1..SN).

First, divide the given array into two parts. Then, in turn, divide the left and right array obtained into two parts and recursively keep dividing them, until they cannot be divided further.

Mathematically,LCP(S1….SN) = LCP(S1….Sk) + LCP(Sk+1…SN), where LCP(S1..SN) is the LCP of the array of strings and 1 < k < N.

Algorithm:

• Recursively divide the input array of strings into two parts.
• For each division, find the LCP obtained so far.
• Merge the obtained LCP from both the subarrays and return it.
• I.e. LCP(LCP(S[left…mid], LCP(S[mid + 1, right])) and return it.

C++ Implementation

Java Implementation

Python Implementation

Time Complexity: O(K) where K is the sum of all the characters in all strings.
Space Complexity: O(M log N), as there are log N recursive calls and each needs a space of M.

Binary Search Approach

Another way to approach the problem is to use the concept of Binary Search.

Algorithm:

• Consider the string with the smallest length. Let the length be L.
• Consider a variable low = 0 and high =  L – 1.
• Perform binary search:
  • Divide the string into two halves, i.e. low – mid and mid + 1 to high.
  • Compare the substring upto the mid of this smallest string to every other character of the remaining strings at that index.
  • If the substring from 0 to mid – 1 is common among all the substrings, update low with mid + 1, else update high with mid – 1
  • If low == high, terminate the algorithm and return the substring from 0 to mid.

C++ Implementation of Binary Search Approach

Java Implementation of Binary Search Approach

Python Implementation of Binary Search Approach

Time Complexity: O(K. logN) where K is the sum of all the characters in all strings.
Space Complexity: O(1)

Practice Question

Longest Common Prefix

Frequently Asked Questions

What is the best time and space complexity of finding the longest prefix string?
The best time complexity is O(N) and the space complexity is O(1) using the horizontal and vertical scanning approach.

Is the binary search approach better than the other approaches?
No, the binary search takes O(K*logN) time complexity. Hence, it is not the most efficient approach.