Rearrange Array Alternately

Problem Statement

Given a sorted array A[] consisting of N integers. The task is to rearrange the array alternatively i.e. the first element should be maxed value, second should be min value, third should be the second max, fourth should be the second min, and so on.

Examples:
Input: A[] = {1, 2, 3, 4, 5, 6, 7}
Output: {7, 1, 6, 2, 5, 3, 4}
Explanation:

Input: A[] = {1, 2, 3, 4, 5, 6}
Output: {6, 1, 5, 2, 4, 3}

Auxiliary Space Approach

The idea is to use a two-pointer approach. The below diagram shows the approach

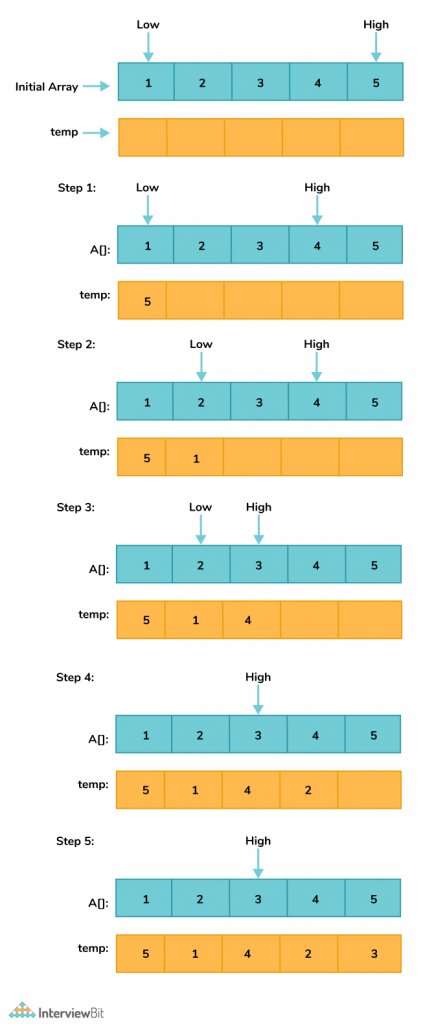
Algorithm

• Consider two pointers low = 0 and high = N – 1, which are pointing to the first and last element of the array.
• Create a temp[] array for storing the resultant array.
• Start copying the last element of the array followed by the first element and so on into the temp array.
• Repeat the above process, until the low pointer becomes less than or equal to the high pointer.

C++ Code For Auxiliary Space Approach

 
void rearrange(int A[], int N)
{
    int temp[N];
    int low = 0, high = N - 1;
    int flag = true;
    
    for (int i = 0; i < N; i++) {
        if (flag)
            temp[i] = A[high--];
        else
            temp[i] = A[low++];
 
        flag = !flag;
    }
    for (int i = 0; i < N; i++)
        A[i] = temp[i];
}

Java Code For Auxiliary Space Approach

static void rearrange(int[] A, int N)
    {
        int temp[] = A.clone();
        int low = 0, high = N - 1;
        boolean flag = true;
 
        // Store result in temp[]
        for (int i = 0; i < N; i++) {
            if (flag)
                A[i] = temp[high--];
            else
                A[i] = temp[low++];
 
            flag = !flag;
        }
    }

Python Code For Auxiliary Space Approach

def rearrange(A, N):
    temp = N*[None]
    low, high = 0, N - 1
 
    flag = True
 
    for i in range(N):
        if flag is True:
            temp[i] = A[high]
            high -= 1
        else:
            temp[i] = A[low]
            low += 1
 
        flag = bool(1-flag)
 
    for i in range(N):
        A[i] = temp[i]
    return A

Time Complexity: O(N) where N is the size of the array A[].
Space Complexity: O(N), as extra space, is used.

Constant Space Approach – Efficient Approach

The efficient approach solves the problem in place without considering any auxiliary array.

The idea is to use multiplication and modular tricks to store two elements at the same index. Observe the below example

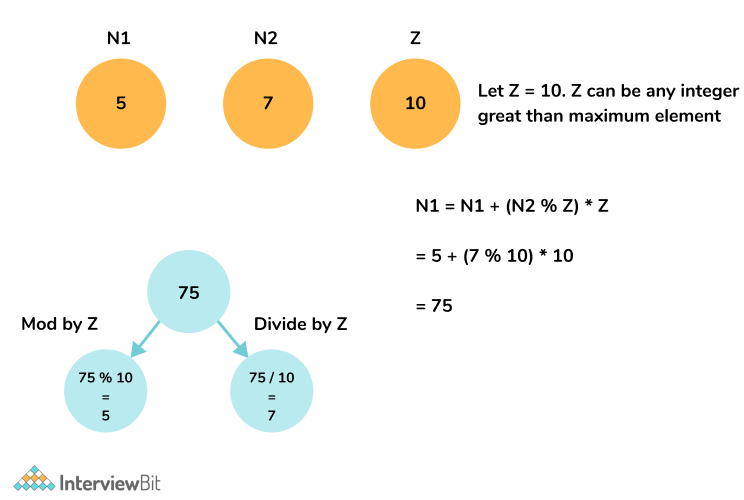
We will use the same approach to solve the problem.

Algorithm

• Initialize two pointers max_idx = N – 1 and min_idx =0 , where N is the size of the array.
• Initialise an element mx equal to 1 + maximum element of the array. Note: You can initialise mx to any integer greater than the maximum element. 
• Iterate over the array and perform the following operations:
  • If the current index is even:
    • Update A[i] = A[i] + (A[max_idx] % mx) * mx
    • Decrement max_idx by 1.
  • If the current index is odd:
    • Update A[i] = A[i] + (A[min_idx] % mx) * mx
    • Increment min_idx by 1.
• To update the array element back to its original form, divide A[i] by mx.

C++ Code For Constant Space Approach

void rearrange(int A[], int N)
{
    int max_idx = N - 1, min_idx = 0;
    int max_elem = A[N - 1] + 1;
    for (int i = 0; i < N; i++) {
        if (i % 2 == 0) {
            A[i] += (A[max_idx] % max_elem) * max_elem;
            max_idx--;
        }
        else {
            A[i] += (A[min_idx] % max_elem) * max_elem;
            min_idx++;
        }
    }
    for (int i = 0; i < N; i++)
        A[i] = A[i] / max_elem;
}

Java Code For Constant Space Approach

public static void rearrange(int A[], int N){
        int max_idx = N - 1, min_idx = 0;
        int mx = A[N - 1] + 1;
        for (int i = 0; i < N; i++) {
            if (i % 2 == 0) {
                A[i] += (A[max_idx] % mx) * mx;
                max_idx--;
            }
            else {
                A[i] += (A[min_idx] % mx) * mx;
                min_idx++;
            }
        }
        for (int i = 0; i < N; i++)
            A[i] = A[i] / mx;
    }

Python Code For Constant Space Approach

def rearrange(A, N):
    max_idx = N - 1
    min_idx = 0
 
    mx = A[N-1] + 1
 
    for i in range(0, N) :
        if i % 2 == 0 :
            A[i] += (A[max_idx] % mx ) * mx
            max_idx -= 1
 
        else :
            A[i] += (A[min_idx] % mx ) * mx
            min_idx += 1
 
    for i in range(0, N) :
        A[i] = A[i] / mx

Time Complexity: O(N) where N is the size of the array A[].
Space Complexity: O(1), as no extra space is used.

Practice Question

Rearrange Array

Frequently Asked Questions

What is the time and complexity of arranging in max-min form?
The time complexity is O(N). The space complexity is O(N) for the naive approach and O(1) using the efficient approach.

Do you need to sort the array A[]?
If the given array is unsorted, then we need to sort the array first and then apply the given approach.