Longest Palindromic Subsequence (With Solution)

Problem Statement

Given a string S, find the common palindromic sequence ( A sequence that does not need to be contiguous and is a palindrome), which is common in itself.

You need to return the length of the longest palindromic subsequence in A.

A string is said to be palindrome if the reverse of the string is the same as the string. For example, “abba” is a palindrome, but “abbc” is not a palindrome.

Examples:

Input: S = “BEBEEED”
Output: 4
Explanation:

The longest common palindromic subsequence is “EEEE”, which has a length of 4

Input: S = “AABCDEBAZ”
Output: 5

Brute force: Recursion Approach

A simple approach to solve this problem is to generate all the subsequences of the given string and find the longest palindromic string among all the generated strings. There are a total of 2^N strings possible, where N denotes the length of the given string.

The idea is to check and compare the first and last characters of the string. There are only two possibilities for the same:

• If the first and the last characters are the same, it can be ensured that both the characters can be considered in the final palindrome and hence, add 2 to the result, since we have found a sequence of length 2 and recurse the remaining substring S[i + 1, j – 1].
• In case, the first and the last characters aren’t the same, the following operation must be performed:
  • Recurse S[i + 1, j]
  • Recurse S[ i, j  – 1]
• Find the maximum length obtained amongst them.

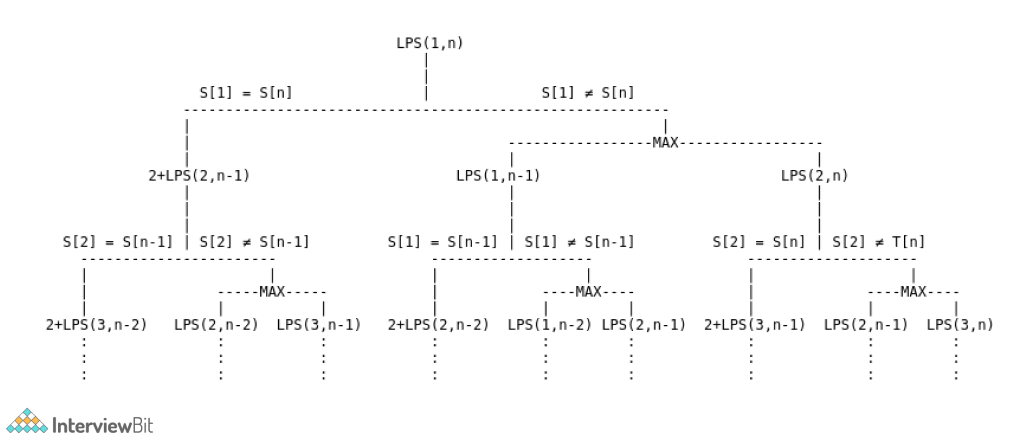
The recursion tree can be shown as follows: LPS(1, N) denotes the length of the longest palindromic subsequence of the given string S[1..N].

C++ Implementation

int LPS(string S, int left, int right){
        if (left > right) {
            return 0;
        } 
        if(left == right){
            return 1;
        }   
        if (S[left] == S[right])
        {
            return 2 + LPS(str,left+1,right-1);
        }
  
  
     return max(LPS(S, left, right - 1), LPS(S, left + 1, right));
    }

Practice on our C++ Compiler

Java Implementation

 static int LPS(String S, int left, int right){
        if (left > right) {
            return 0;
        } 
        if(left == right){
            return 1;
        }   
        if (S.charAt(left) == S.charAt(right) )
        {
            return 2 + LPS(str,left+1,right-1);
        }
  
  
     return Math.max(LPS(S, left, right - 1), LPS(S, left + 1, right));
    }

Practice on our Java Compiler

Python Implementation

def LPS(S, left, right){
        if left > right:
            return 0
        If left == right:
            return 1
        
        if S[left] == S[right]:
            return 2 + LPS(str,left+1,right-1);
  
  
       return max(LPS(S, left, right - 1), LPS(S, left + 1, right))

Practice on our Python Compiler

Time Complexity: O(2^N) where N is the size of the string S.
Space Complexity: O(1), as no extra space is used.

Efficient Approach (Using Dynamic Programming)

The efficient approach uses a dynamic programming approach for the problem.

It can be clearly observed that some of the subsequences are repeating i.e it contains overlapping subproblems. Let us take the example of the string ABCDE.

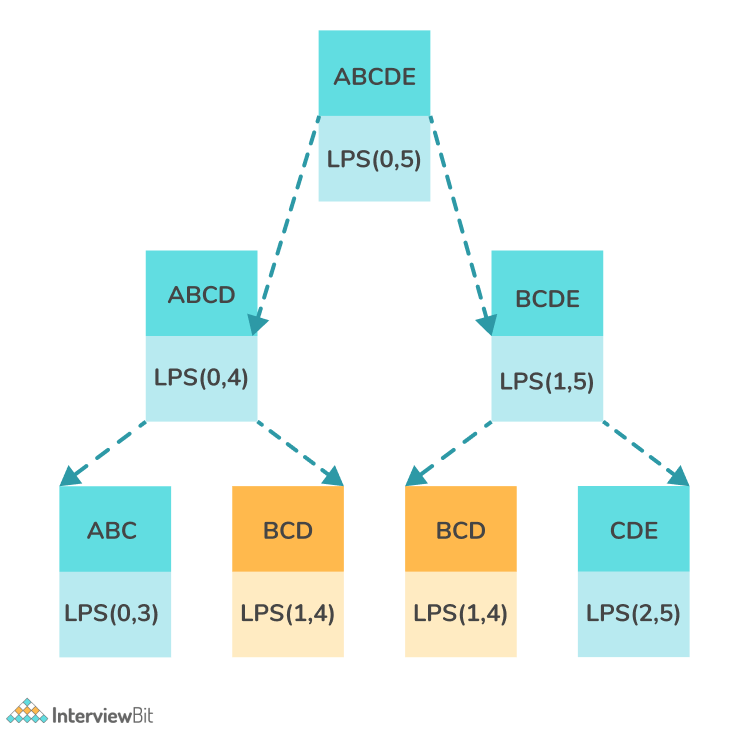
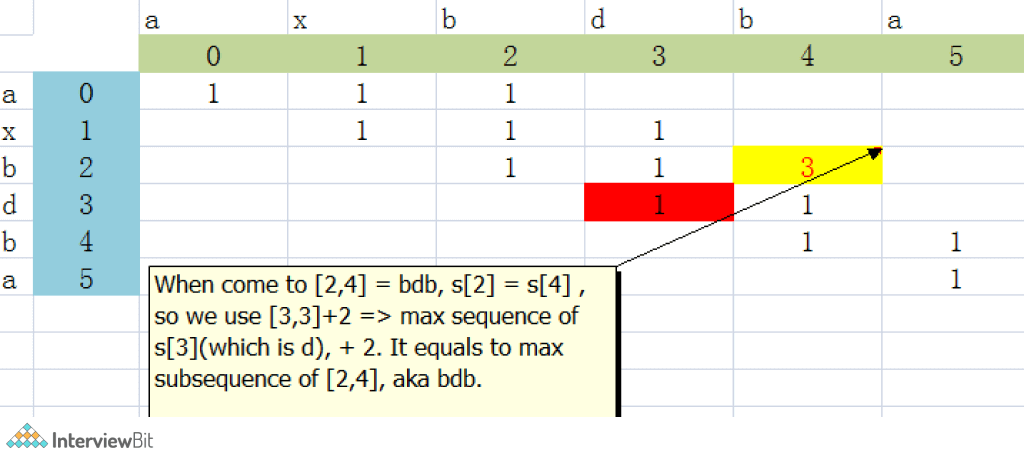
The subproblems BCD is repeating twice, hence instead of calculating the value twice, we can instead store it in a table. Let’s illustrate the algorithm with the string – “axbdba”.

Consider a dp array of size N * N.

Algorithm:

Fill the table with a start case, dp[i, i] == 1, since all single char in a string is a palindrome, which length is 1.

When s[i] == s[j]

When s[i] == s[j]

Continue the process until the whole dp array is filled.

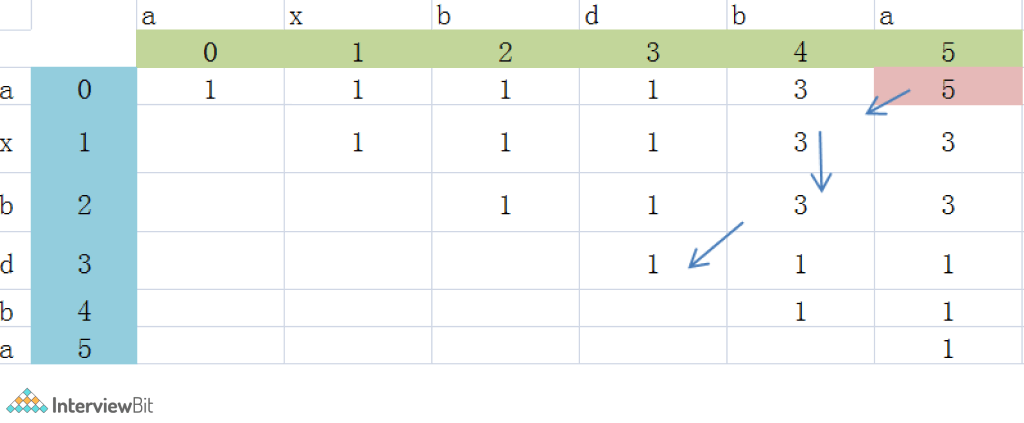
Return dp[0][N  – 1] is the longest palindromic subsequence(LPS)

C++ Code for DP Approach

public int LPS(string S) {
        int dp[S.length()][S.length()];
        
        for (int i = S.length() - 1; i >= 0; i--) {
            dp[i][i] = 1;
            for (int j = i+1; j < S.length(); j++) {
                if (S[i] == S[j]) {
                    dp[i][j] = dp[i+1][j-1] + 2;
                } else {
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        return dp[0][S.length()-1];
 }

Java Code for DP Approach

public int LPS(String S) {
        int[][] dp = new int[S.length()][S.length()];
        
        for (int i = S.length() - 1; i >= 0; i--) {
            dp[i][i] = 1;
            for (int j = i+1; j < S.length(); j++) {
                if (S.charAt(i) == S.charAt(j)) {
                    dp[i][j] = dp[i+1][j-1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        return dp[0][S.length()-1];
 }

Python Code for DP Approach

def LPS(S):
        dp = [[0 for x in range(len(S))] for x in range(len(S))]
        
        for i in range(len(S) - 1, -1, -1):
            dp[i][i] = 1;
            for j in range(i + 1, len(S)):
                if S[i] == S[j]:
                    dp[i][j] = dp[i+1][j-1] + 2;
                 
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
                
            
        return dp[0][S.length()-1];

Time Complexity: O(N^2) where N is the size of the string S.
Space Complexity: O(N^2), as extra dp array is used.

Practice Question

Longest Palindromic Subsequence

Frequently Asked Questions

How to find the longest palindromic subsequence?
The LPS can be calculated efficiently using the dynamic programming approach, which can be solved in O(N^2), where N is the size of the given string.

How to find the palindromic subsequence from the table?
To find the subsequence, which gives us the longest LPS, backtrack from dp[0][N – 1] and trace the path back to dp[0][0].