Number of Pairs

Problem Statement

Given two integer arrays A[] and B[] of size N and M respectively. The task is to count the number of pairs (x, y) such that x^y > y^x, where x is an element of array A[], while y is an element of array B[].

Examples:

Input: A[] = {2, 1, 6}, B[] = {1, 5}
Output: 3
Explanation:
There are three possible pairs :

• (2, 1)  : 2 ^ 1 > 1 ^ 2
• (6, 1) : 6 ^ 1 > 1 ^ 6
• (2, 5) : 2 ^ 5 > 5 ^ 2

Input: A[] = {1, 2, 3}, B[] = {4, 5, 6, 7};
Output: 7

Brute Force Approach

The simplest approach is to run two nested loops over the arrays A[] and B[] and if any of the pairs satisfy the above condition, increment the count.

C++ Implementation of Brute Force Approach

int countPairs(int A[], int B[], int N, int M) 
{ 
    int count = 0; 
    for (int i = 0; i < N; i++){ 
       for (int j = 0; j < M; j++){
          if (pow(A[i], B[j]) > pow(B[j], A[i])){
              count++; 
          }
       }
    }
    return ans; 
}

Java Implementation of Brute Force Approach

countPairs(int[] A, int[] B, int N, int M) 
{ 
    int count = 0; 
    for (int i = 0; i < N; i++){ 
       for (int j = 0; j < M; j++){
          if (Math.pow(A[i], B[j]) > Math.pow(B[j], A[i])){
              count++; 
          }
       }
    }
    return ans; 
}

Python Implementation of Brute Force Approach

def countPairs(A, B, N, M) 
{ 
     count = 0; 
     for i in range(N):
        for j in range(M):
          if (A[i]**B[j] > B[j]**A[i])){
              count = count + 1; 
          
    return ans; 
}

Time Complexity: O(N * M) where N and M are the size of the A[] and B[].
Space Complexity: O(1), as no extra space is used.

Efficient Approach (Using binary search)

The trick to solving this problem is based on the fact that, for a pair (X, Y), if Y > X,
then X ^ Y > Y ^ X.

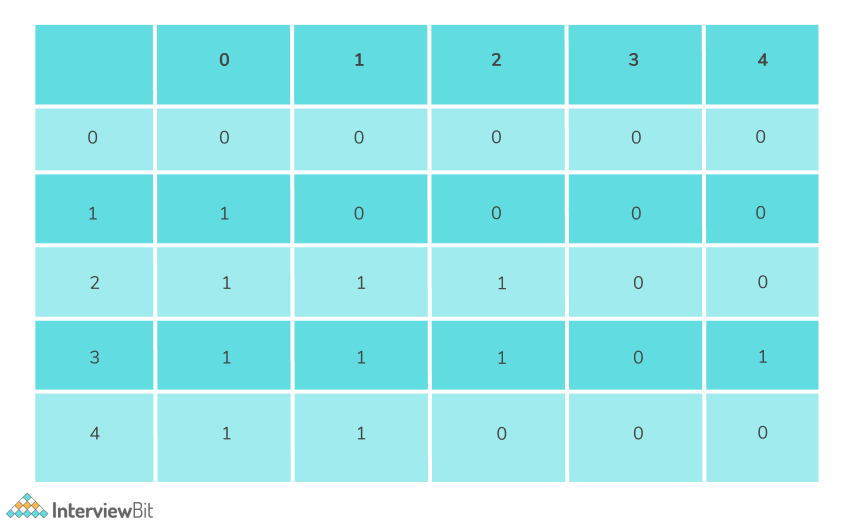
There are a few exceptions, for which this condition fails.

• If X = 0, then RHS is always 1 i.e. 0 ^ Y < Y ^ 0, hence the count for this case is 0.
• If X = 1, then total pairs is equal to the number of 0’s in the array B[]. This is based on the fact that 1 ^ 0 > 0 ^ 1, but 0 < 1.
• If X = 2. but  Y = 3 or Y = 4, the condition fails, as 2 ^ 3 < 3 ^3. Similarly, 2 ^ 4 == 4 ^2

If X = 3, but  Y = 2, we need to consider it since, 3 ^ 2 > 2 ^3 but 2 < 3.

The exceptions can be shown in tabular format as follows:

Algorithm

• Sort the array B[].
• Consider a frequency array to count the frequency of 0, 1, 2, 3, 4 in array B[].
• For every ith element of A[], find the index, idx of the smallest element greater than A[i] in B[] using binary search.
• To handle the exceptions, follow the below approach:
  • If, A[i] = 0, count = 0
  • If, A[i] = 1, count = freq[1] in B[].
  • If, A[i] = 2, decrement count by frequency of 3 and 4 in B[].
  • If, A[i] = 3, increment count by frequency of 2 in B[].
• All the integers, after index idx satisfies the above condition, hence count should be incremented by N – idx.
• Return count.

C++ Code

int count(int x, int B[], int N, int freq[])
{
    if (x == 0)
        return 0;
 
    if (x == 1)
        return freq[0];
 
    int* idx = upper_bound(B, B + M, x);
    int countx = (B + M) - idx;
 
    countx += (freq[0] + freq[1]);
 
    if (x == 2)
        countx -= (freq[3] + freq[4]);
 
    if (x == 3)
        countx += freq[2];
 
    return countx;
}
 
int countPairs(int A[], int B[], int N, int M)
{
    int freq[5] = { 0 };
    for (int i = 0; i < M; i++)
        if (B[i] < 5)
            freq[Y[i]]++;
 
    sort(B, B + M);
 
    int total_pairs = 0;
 
    for (int i = 0; i < N; i++)
        total_pairs += count(A[i], B, M, freq);
 
    return total_pairs;
}

Java Code

count(int x, int B[], int M, int freq[]){
 
        if (x == 0)
            return 0;
 
        if (x == 1)
            return freq[0];
 
        int idx = Arrays.binarySearch(B, x);
        int countx = 0;
        if (idx < 0) {
            idx = Math.abs(idx + 1);
            countx = Y.length - idx;
        }
        else {
            while (idx < n && Y[idx] == x) {
                idx++;
            }
            countx = M - idx;
        }
        countx += (freq[0] + freq[1]);
 
        if (x == 2)
            countx -= (freq[3] + freq[4]);
 
        if (x == 3)
            countx += freq[2];
 
        return countx;
    }
 
    countPairs(int A[], int B[], int N, int M)
    {
        int freq[] = new int[5];
        for (int i = 0; i < M; i++)
            if (B[i] < 5)
                freq[Y[i]]++;
 
 
        Arrays.sort(B);
 
        long total_pairs = 0;
 
        for (int i = 0; i < N; i++)
            total_pairs += count(A[i], B, M, freq);
 
        return total_pairs;
    }

Python Code

import bisect
def count(x, B , n, freq):
    if x == 0:
        return 0
 
    if x == 1:
        return freq[0]
 
    idx = bisect.bisect_right(B, x)
    countx = n - idx
 
    ans += freq[0] + freq[1]
    if x == 2:
        countx -= freq[3] + freq[4]
 
    if x == 3:
        countx += freq[2]
 
    return ans
 
def count_pairs(A, B, N, M):
 
    freq = [0] * 5
    for i in range(M):
        if B[i] < 5:
            freq[B[i]] += 1
 
    B.sort()
    total_pairs = 0 
 
    for x in A:
        total_pairs += count(x, B, M, freq)
 
    return total_pairs

Time Complexity: O(N * log N + M * log M), where N and M are the size of the A[] and B[].Space Complexity: O(1)

Practice Questions

Pairs With Given XOR
Pair With Given Difference

Frequently Asked Questions

What is the time complexity of the above approach?
The time complexity is O(NlogN + MlogM), where N and M are the size of arrays A[] and B[]  respectively.

Why do you need to sort the array B[]?
Since we are applying binary search on array B, to count the smallest index greater than A[i], and binary search works on sorted arrays, we need to sort array B[].