Lowest Common Ancestor

The Lowest Common Ancestor of two nodes is the lowest node that has both nodes as descendants.

Problem Statement

Given a binary tree of integers. The task is to find the Lowest Common Ancestor of two nodes in the given tree.

Examples

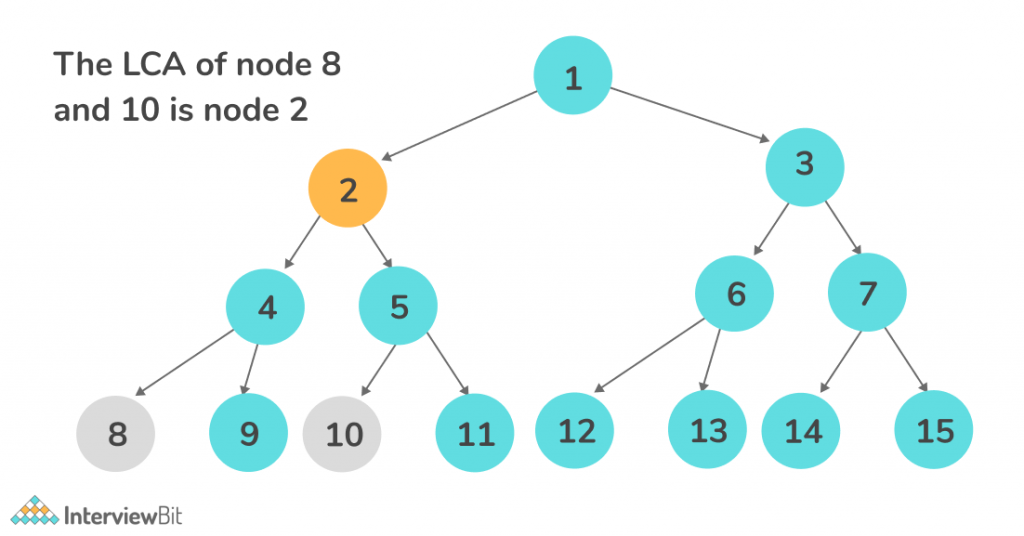
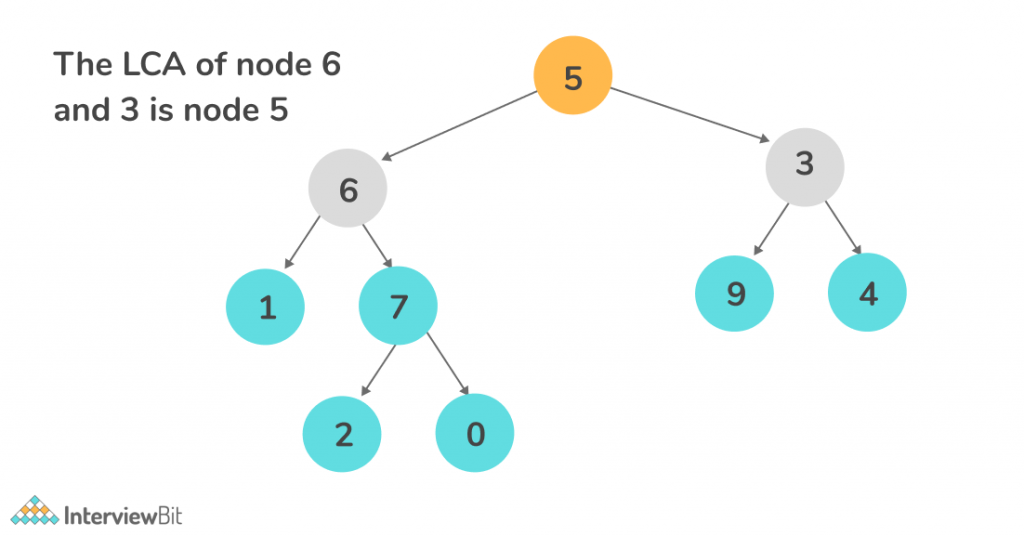
Recursive Approach

The idea is to traverse the binary tree in a depth-first approach and search for both nodes in the binary tree. The LCA of both nodes is the node, for which the recursion on the subtree returns the same node.

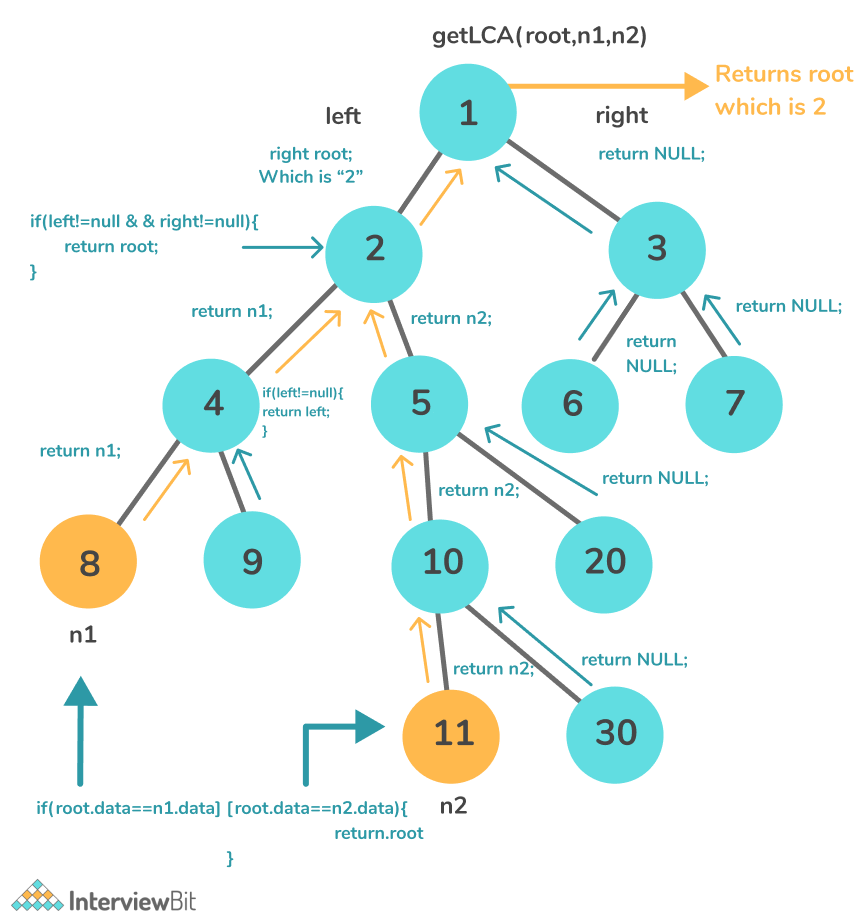
Algorithm

• Start from the DFS from the root of the binary tree.
• Recurse the left and right subtree.
• If the current nodes visited is any of the given nodes whose LCA is to be found, return that node.
• Else, for both the nodes, if the subtree provides the same non NULL node, it is the LCA, hence return the node.

C++ Code Implementation

struct Node * findLCA(struct Node * root, int n1, int n2) {
  if (root == NULL) return NULL;
  if (root -> key == n1 || root -> key == n2)
    return root;
 
  Node * left_lca = findLCA(root -> left, n1, n2);
  Node * right_lca = findLCA(root -> right, n1, n2);
 
  if (left_lca && right_lca) return root;
 
  return (left_lca != NULL) ? left_lca : right_lca;
}

Java Code Implementation

Node root;
 
Node findLCA(int n1, int n2) {
  return findLCA(root, n1, n2);
}
Node findLCA(Node node, int n1, int n2) {
  if (node == null)
    return null;
 
  if (node.data == n1 || node.data == n2)
    return node;
 
  Node left_lca = findLCA(node.left, n1, n2);
  Node right_lca = findLCA(node.right, n1, n2);
 
  if (left_lca != null && right_lca != null)
    return node;
 
  return (left_lca != null) ? left_lca : right_lca;
}

Python Code Implementation

def findLCA(root, n1, n2):
 
    if root is None:
        return None
 
    if root.key == n1 or root.key == n2:
        return root
 
    left_lca = findLCA(root.left, n1, n2)
    right_lca = findLCA(root.right, n1, n2)
 
    if left_lca and right_lca:
        return root
 
    return left_lca if left_lca is not None else right_lca

• Time Complexity: O(N) where N is the number of nodes of the binary tree.
• Space Complexity: O(N), because of the recursive stack.

Approach 2 (Iterative)

The iterative approach to solve this problem is to use parent pointers. The idea is to establish parent pointers for each node so that we can traverse back from the nodes to get their descendants.

Algorithm

• Start traversing from the root node.
• For each node visited, keep storing the parent pointers in a map.
• Continue, until both the given nodes are found.
• Since all parent points for each node are stored now, traverse back for node1. Similarly, for node2, traverse back through the parent pointers.
• If at any point, the same ancestor appears for both nodes, return that node, since it is the LCA of both nodes.
• Else, continue traversing.

C++ Code Implementation

Node * LCA(Node * n1, Node * n2) {
  map < Node * , bool > ancestors;
  while (n1 != NULL) {
    ancestors[n1] = true;
    n1 = n1 -> parent;
  }
  while (n2 != NULL) {
    if (ancestors.find(n2) != ancestors.end())
      return n2;
    n2 = n2 -> parent;
  }
 
  return NULL;
}

Java Code Implementation

Node LCA(Node n1, Node n2) {
  Map < Node, Boolean > ancestors = new HashMap < Node, Boolean > ();
  while (n1 != null) {
    ancestors.put(n1, Boolean.TRUE);
    n1 = n1.parent;
  }
  while (n2 != null) {
    if (ancestors.containsKey(n2) != ancestors.isEmpty())
      return n2;
    n2 = n2.parent;
  }
 
  return null;
}

Python Code Implementation

def find_lca(n1, n2):
    seen_on_path: Set[BinaryTreeNode] = set()
 
    while n1 or n2:
 
        if n1:
            if n1 in seen_on_path:
                return n1
            seen_on_path.add(n1)
            n1 = n1.parent
 
        if n2:
            if n2 in seen_on_path:
                return n2
            seen_on_path.add(n2)
            n2 = n2.parent
    return None

• Time Complexity: O(N) where N is the number of nodes of the binary tree.
• Space Complexity: O(N), as a map is used.

Practice Question

1. Least Common Ancestor

FAQs

Q.1: What will happen if the tree is a BST?

Ans: Though the time complexity will remain the same, for BST, fewer checks need to be done, as we know can apply the property of BST.

Q.2: Why is a Hashmap used?

Ans: The hashmap is used to store the parent pointers of all the nodes so that the nodes can be traversed back and the common ancestors can be found.