Problem Statement
Given a 2D matrix, find the largest possible sum submatrix in it and print its value.
Submatrix: In this problem, a submatrix is defined as a rectangle, which can be obtained by deleting a certain number of boundary rows and columns from the given original matrix. All elements of the rectangle need to be contiguous either row-wise or column-wise.
Sample Test Cases :
Input 1:
Matrix =
{{1, 2, -1, -4, -20},
{-8, -3, 4, 2, 1},
{3, 8, 10, 1, 3},
{-4, -1, 1, 7, -6}}
Confused about your next job?
Output 1:
(top, left) : (1, 1)
(bottom, right) : (3, 3)
29
Explanation 1:
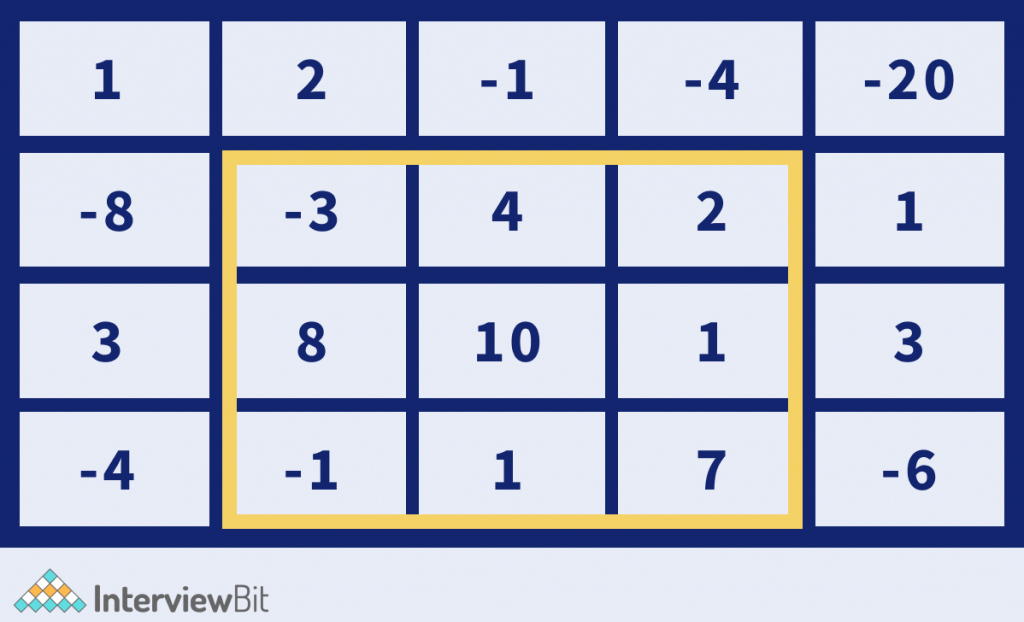
We can observe from the image that the shaded submatrix denotes the maximum sum rectangle in the above example. The sum of elements in this submatrix gives us a value of 29.
Input 2:
Matrix =
{{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0}}
Output 2:
(top, left) : (0, 0)
(bottom, right) : (3, 4)
10
Explanation 2: The entire matrix will correspond to the maximum sum rectangle for this matrix.
Naive Approach
The naive approach is to iterate over all the submatrices of the matrix and calculate the maximum rectangle sum over all the submatrices. We will use 4 nested loops to fix the corners of the rectangle/submatrix, and then another 2 nested loops to calculate the sum of that submatrix.
C++ Implementation
void maxMatrixSum(vector < vector < int >> & matrix) {
int n = matrix.size();
int m = matrix[0].size();
int maxSum = INT_MIN;
int top = 0, bottom = 0, left = 0, right = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
for (int k = 0; k < n; k++) {
for (int l = 0; l < m; l++) {
int currSum = 0;
for (int x = i; x <= k; x++) {
for (int y = j; y <= l; y++) {
currSum += matrix[x][y];
}
}
if (currSum > maxSum) {
maxSum = currSum;
top = i;
left = j;
right = k;
bottom = l;
}
}
}
}
}
cout << "The Top Left of the rectangle is: " << top << " " << left << endl;
cout << "The Bottom Right of the rectangle is: " << bottom << " " << right << endl;
cout << "The sum of this rectangle is: " << maxSum << endl;
}Java Implementation
public static void maxMatrixSum(int[][] matrix) {
int n = matrix.length;
int m = matrix[0].length;
int maxSum = -999999999;
int top = 0, bottom = 0, left = 0, right = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
for (int k = 0; k < n; k++) {
for (int l = 0; l < m; l++) {
int currSum = 0;
for (int x = i; x <= k; x++) {
for (int y = j; y <= l; y++) {
currSum += matrix[x][y];
}
}
if (currSum > maxSum) {
maxSum = currSum;
top = i;
left = j;
right = k;
bottom = l;
}
}
}
}
}
System.out.println("The Top Left of the rectangle is: " + top + " " + left);
System.out.println("The Bottom Right of the rectangle is: " + bottom + " " + right);
System.out.println("The sum of the rectangle is: " + maxSum);
}Python Implementation
def maxMatrixSum(matrix):
maxSum = -9999999
n = len(matrix)
m = len(matrix[0])
top, left, right, bottom = None, None, None, None
for i in range(n):
for j in range(m):
for k in range(n):
for l in range(m):
currSum = 0
for x in range(i, k + 1):
for y in range(j, l + 1):
currSum += matrix[x][y]
if currSum > maxSum:
maxSum = currSum
top = i
left = j
right = k
bottom = l
print("The Top Left of the Rectangle is: ", top, left)
print("The Bottom Right of the Rectangle is: ", bottom, right)
print("The maximum sum is: ", maxSum)Complexity Analysis
- Time Complexity: O(n6)
- Space Complexity: O(1)
Optimal Approach
We will use Kadane’s Algorithm for finding the largest sum subarray (in 1D) to improve our time complexity over the naive approach. The key idea in this approach is that we will fix the left and right columns one by one and then for contiguous rows, we will find the maximum sum, for all possible choices of left and right column pairs with the help of Kadane’s Algorithm. The algorithm is as follows:
- Store the sum of elements in each row, from column, numbered left to right, in an array (stored[])
- By applying Kadane’s Algorithm in this stored[] array, we will obtain the maximum sum subarray of this array, which is equal to the maximum sum, that can be obtained with column boundaries from left to right.
- To obtain the overall maximum sum, we take the maximum of all such values of sums obtained so far till the algorithm terminates.

C++ Code
int kadaneAlgorithm(vector < int > & a, int & start, int & end, int n) {
int currSum = 0, maxSum = INT_MIN;
end = -1;
int currStart = 0;
for (int i = 0; i < n; i++) {
currSum += a[i];
if (currSum < 0) {
currSum = 0;
currStart = i + 1;
} else if (maxSum < currSum) {
maxSum = currSum;
start = currStart;
end = i;
}
}
if (end != -1) {
return maxSum;
}
int index = max_element(a.begin(), a.end()) - a.begin();
start = end = index;
maxSum = * max_element(a.begin(), a.end());
return maxSum;
}
void maxMatrixSum(vector < vector < int >> & matrix) {
int n = matrix.size();
int m = matrix[0].size();
int matrixLeft = -1, matrixRight = -1, matrixTop = -1, matrixBottom = -1;
int maxSum = INT_MIN;
vector < int > stored(n);
int sum, start, end;
for (int left = 0; left < m; left++) {
stored.assign(n, 0);
for (int right = left; right < m; right++) {
for (int i = 0; i < n; i++) {
stored[i] += matrix[i][right];
}
sum = kadaneAlgorithm(stored, start, end, n);
if (maxSum < sum) {
maxSum = sum;
matrixLeft = left;
matrixRight = right;
matrixTop = start;
matrixBottom = end;
}
}
}
cout << "The Top Left of the rectangle is: " << matrixTop << " " << matrixLeft << endl;
cout << "The Bottom Right of the rectangle is: " << matrixBottom << " " << matrixRight << endl;
cout << "The sum of this rectangle is: " << maxSum << endl;
}Java Code
public static void maxMatrixSum(int[][] matrix) {
int n = matrix.length;
int m = matrix[0].length;
int matrixLeft = -1, matrixRight = -1, matrixTop = -1, matrixBottom = -1;
int maxSum = Integer.MIN_VALUE;
int[] stored = new int[n];
int sum, start = 0, end;
for (int left = 0; left < m; left++) {
Arrays.fill(stored, 0);
for (int right = left; right < m; right++) {
for (int i = 0; i < n; i++) {
stored[i] += matrix[i][right];
}
int currSum = 0, greatestSum = Integer.MIN_VALUE;
end = -1;
int currStart = 0;
for (int i = 0; i < n; i++) {
currSum += stored[i];
if (currSum < 0) {
currSum = 0;
currStart = i + 1;
} else if (maxSum < currSum) {
greatestSum = currSum;
start = currStart;
end = i;
}
}
if (end != -1) {
sum = greatestSum;
} else {
start = 0;
end = 0;
greatestSum = stored[0];
for (int i = 0; i < n; i++) {
if (greatestSum < stored[i]) {
greatestSum = stored[i];
start = i;
end = i;
}
}
sum = greatestSum;
}
if (maxSum < sum) {
maxSum = sum;
matrixLeft = left;
matrixRight = right;
matrixTop = start;
matrixBottom = end;
}
}
}
System.out.println("The Top Left of the rectangle is: " + matrixTop + " " + matrixLeft);
System.out.println("The Bottom Right of the rectangle is: " + matrixBottom + " " + matrixRight);
System.out.println("The sum of the rectangle is: " + maxSum);
}Python Code
def kadaneAlgorithm(a, start, end, n):
currSum = 0
maxSum = -9999999
end[0] = -1
currStart = 0
for i in range(n):
currSum += a[i]
if currSum < 0:
currSum = 0
currStart = i + 1
elif maxSum < currSum:
maxSum = currSum
start[0] = currStart
end[0] = i
if end[0] != -1:
return maxSum
maxSum = max(a)
for i in range(n):
if maxSum == a[i]:
start = i
end = i
return maxSum
def maxMatrixSum(matrix):
maxSum = -9999999
matrixLeft, matrixRight, matrixTop, matrixBottom = None, None, None, None
n = len(matrix)
m = len(matrix[0])
stored = [0] * n
sum = 0
start = [0]
end = [0]
for left in range(m):
stored = [0] * n
for right in range(left, m):
for i in range(n):
stored[i] += matrix[i][right]
sum = kadaneAlgorithm(stored, start, end, n)
if sum > maxSum:
maxSum = sum
matrixLeft = left
matrixRight = right
matrixTop = start[0]
matrixBottom = end[0]
print("The Top Left of the Rectangle is: ", matrixTop, matrixLeft)
print("The Bottom Right of the Rectangle is: ", matrixBottom, matrixRight)
print("The maximum sum is: ", maxSum)Complexity Analysis
- Time Complexity: O(n3)
- Space Complexity: O(n)
Practice Problem
FAQs
Q. What is Kadane’s Algorithm used for?
A. Kadane’s Algorithm is used to find the largest sum subarray in a 1D array or list.
Q. Will this algorithm work if all the array elements are negative?
A. Yes, even in that case the algorithm will work, and the result should be equal to the largest number in the array.




