Problem Statement
Given an n * m grid, where each element can contain one of the 3 given values,
- 0 represents an empty cell.
- 1 represents a cell containing fresh orange.
- 2 represents a cell containing rotten orange.
Every day, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of days that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Confused about your next job?
Sample Test Cases
Input 1:
grid = [[2, 1, 0],
[1, 1, 0], [0, 1, 1]]Output 1:
4
Explanation 1:
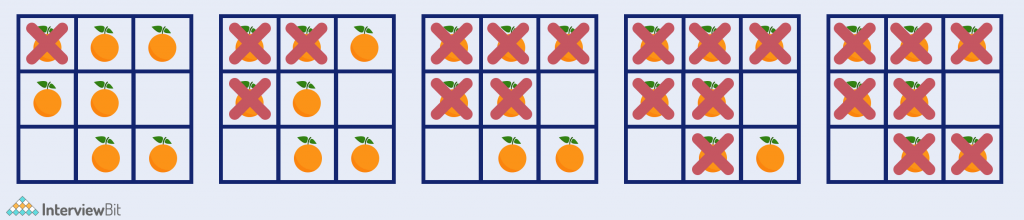
From the figure, we see that on the 4th day, all the oranges get rotten.
Input 2:
grid = [[2, 1, 0],
[1, 1, 0], [1, 0, 1]]Output 2:
-1
Explanation 2:
The orange at (2, 0) will never get rotten.
Approach
Naive Approach:
In the naive approach, we can traverse through all the oranges in the grid in multiple rounds.
In each round, we can rot the oranges to adjacent positions of oranges that had gotten rotten in the previous round. The algorithm is as follows:
- Create variables days and flag and initialize them to 2 and false respectively.
- We run an infinite loop that will continue until there is no cell in the grid, which is changed in the current iteration.
- Traverse through every element of the grid and if the elements of the matrix are equal to days and its adjacent elements values are 1, then update them to days + 1. Also, set the flag to true.
- Search for a cell containing value 1, by traversing the matrix. If found return -1.
- Else return days – 2.
Code / Implementation:
C++ Code
bool isSafe(vector < vector < int >> & grid, int i, int j) {
int n = grid.size();
int m = grid[0].size();
return (i >= 0 && j >= 0 && i < n && j < m);
}
int numberOfDays(vector < vector < int >> & grid) {
int days = 2;
bool flag = false;
int n = grid.size();
int m = grid[0].size();
while (1) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == days) {
if (isSafe(grid, i + 1, j) && grid[i + 1][j] == 1) {
grid[i + 1][j] = grid[i][j] + 1;
flag = true;
}
if (isSafe(grid, i, j + 1) && grid[i][j + 1] == 1) {
grid[i][j + 1] = grid[i][j] + 1;
flag = true;
}
if (isSafe(grid, i - 1, j) && grid[i - 1][j] == 1) {
grid[i - 1][j] = grid[i][j] + 1;
flag = true;
}
if (isSafe(grid, i, j - 1) && grid[i][j - 1] == 1) {
grid[i][j - 1] = grid[i][j] + 1;
flag = true;
}
}
}
}
if (flag == false) {
break;
}
flag = false;
days++;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
days = -1;
}
}
}
return days == -1 ? days : days - 2;
}Java Code
public static boolean isSafe(int[][] grid, int i, int j) {
int n = grid.length;
int m = grid[0].length;
return (i >= 0 && j >= 0 && i < n && j < m);
}
public static int numberOfDays(int[][] grid) {
int days = 2;
boolean flag = false;
int n = grid.length;
int m = grid[0].length;
while (true) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == days) {
if (isSafe(grid, i + 1, j) && grid[i + 1][j] == 1) {
grid[i + 1][j] = grid[i][j] + 1;
flag = true;
}
if (isSafe(grid, i, j + 1) && grid[i][j + 1] == 1) {
grid[i][j + 1] = grid[i][j] + 1;
flag = true;
}
if (isSafe(grid, i - 1, j) && grid[i - 1][j] == 1) {
grid[i - 1][j] = grid[i][j] + 1;
flag = true;
}
if (isSafe(grid, i, j - 1) && grid[i][j - 1] == 1) {
grid[i][j - 1] = grid[i][j] + 1;
flag = true;
}
}
}
}
if (flag == false) {
break;
}
flag = false;
days++;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
days = -1;
}
}
}
return days == -1 ? days : days - 2;
}Python Code
def isSafe(grid, i, j):
n = len(grid)
m = len(grid[0])
return i >= 0 and j >= 0 and i < n and j < m
def numberOfDays(grid):
days = 2
flag = False
n = len(grid)
m = len(grid[0])
while 1:
for i in range(n):
for j in range(m):
if grid[i][j] == days:
if isSafe(grid, i + 1, j) and grid[i + 1][j] == 1:
grid[i + 1][j] = grid[i][j] + 1
flag = True
if isSafe(grid, i - 1, j) and grid[i - 1][j] == 1:
grid[i - 1][j] = grid[i][j] + 1
flag = True
if isSafe(grid, i, j + 1) and grid[i][j + 1] == 1:
grid[i][j + 1] = grid[i][j] + 1
flag = True
if isSafe(grid, i, j - 1) and grid[i][j - 1] == 1:
grid[i][j - 1] = grid[i][j] + 1
flag = True
if flag == False:
break
flag = False
days += 1
for i in range(n):
for j in range(m):
if grid[i][j] == 1:
days = -1
return -1 if days == -1 else days - 2Complexity Analysis:
- Time Complexity: O((n * m) * (n * m))
- Space Complexity: O(1)
Optimal Approach:
We can solve this problem optimally using the “Multisource BFS” algorithm on a grid. The key observation is that fresh oranges adjacent to rotten oranges are rotten on day 1, those adjacent to those oranges are rotten on day 2, and so on. The phenomenon is similar to a level order traversal on a graph, where all the initial rotten oranges act as root nodes.
We can just push all these root nodes into a queue and perform BFS on a grid algorithm, to calculate the total time taken to rot all the oranges. If all oranges are not rotten before our algorithm terminates, we will return -1.
The algorithm is described as follows:
- Initialize the number of days to 0.
- Declare a queue of appropriate datatype and push all the cells containing rotten oranges into it one by one.
- While the queue is not empty, pop the cell from the front of the queue, and try to go all its neighbors in 4 directions, keeping check that they lie within the boundary of the matrix, and changing their values to 2(rotten orange). Push all these adjacent into the queue, and continue the algorithm until the next iteration.
- Keep updating the days passed variable appropriately, and continue the algorithm till all the cells are visited.
- Iterate through the grid again and if a cell with a fresh orange is found, return -1.
- Else return the days passed.
Implementation:
C++ Code
const int dx[] = { 1, 0, -1, 0};
const int dy[] = {0, 1, 0, -1};
bool isSafe(vector < vector < int >> & grid, int x, int y) {
int r = grid.size();
int c = grid[0].size();
return (x >= 0 && x < r && y >= 0 && y < c && grid[x][y] == 1);
}
int numberOfDays(vector < vector < int >> & grid) {
int r = grid.size();
int c = grid[0].size();
queue < pair < int, int >> q;
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
if (grid[i][j] == 2) {
q.push({ i, j });
}
}
}
int days = -2;
while (!q.empty()) {
int qs = q.size();
while (qs--) {
pair < int, int > p = q.front();
int x = p.first;
int y = p.second;
q.pop();
for (int i = 0; i < 4; i++) {
if (isSafe(grid, x + dx[i], y + dy[i])) {
q.push({
x + dx[i],
y + dy[i]
});
grid[x + dx[i]][y + dy[i]] = 2;
}
}
}
days += 1;
}
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
if (grid[i][j] == 1) {
return -1;
}
}
}
return days == -2 ? 0 : days + 1;
}Java Code
static int dx[] = {1, 0, -1, 0};
static int dy[] = {0, 1, 0, -1};
public static int numberOfDays(int[][] grid) {
int r = grid.length;
int c = grid[0].length;
int days = 0, countOfOnes = 0;
Queue < int[] > q = new LinkedList < > ();
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
if (grid[i][j] == 2) {
q.add(new int[] {i, j});
}
if (grid[i][j] == 1) {
countOfOnes += 1;
}
}
}
if (countOfOnes == 0) {
return 0;
}
while (!q.isEmpty()) {
int size = q.size();
while (size--> 0) {
int[] temp = q.remove();
int i = temp[0], j = temp[1];
for (int l = 0; l < 4; l++) {
int nr = i + dx[l], nc = j + dy[l];
if (nr < 0 || nc < 0 || nr == r || nc == c) {
continue;
}
if (grid[nr][nc] == 1) {
countOfOnes -= 1;
q.add(new int[] {
nr,
nc
});
grid[nr][nc] = 2;
}
}
}
if (q.size() > 0) {
days += 1;
}
}
return countOfOnes == 0 ? days : -1;
}Python Code
def numberOfDays(grid):
r = len(grid)
c = len(grid[0])
fresh = 0
queue = []
vis = set()
for i in range(r):
for j in range(c):
if grid[i][j] == 2:
queue.append((i, j, 0))
vis.add((i, j))
elif grid[i][j] == 1:
fresh += 1
if not fresh:
return 0
while queue:
size = len(queue)
while size:
x, y, days = queue.pop(0)
if x < r - 1 and (x + 1, y) not in vis and grid[x + 1][y] == 1:
queue.append((x + 1, y, days + 1))
vis.add((x + 1, y))
fresh -= 1
if x > 0 and (x - 1, y) not in vis and grid[x - 1][y] == 1:
queue.append((x - 1, y, days + 1))
vis.add((x - 1, y))
fresh -= 1
if y < c - 1 and (x, y + 1) not in vis and grid[x][y + 1] == 1:
queue.append((x, y + 1, days + 1))
vis.add((x, y + 1))
fresh -= 1
if y > 0 and (x, y - 1) not in vis and grid[x][y - 1] == 1:
queue.append((x, y - 1, days + 1))
vis.add((x, y - 1))
fresh -= 1
size -= 1
return -1 if fresh else daysComplexity Analysis:
- Time Complexity: O(n * m)
- Space Complexity: O(n * m)
FAQs
1. What is the main insight which can be learned from this problem?
A. The key insight to learn from this problem is to learn how to model a seemingly unrelated problem into a graph traversal problem.
2. What is the difference between Single Source and Multi-Source BFS?
A. The difference is as the name suggests, in multi-source BFS, multiple nodes act as the root node of the graph network simultaneously.