Problem Statement
Given N intervals, where each interval denotes startTime and endTime. The task is to merge all overlapping intervals possible and return a list of overlapping intervals in sorted order of their startTime.
Examples:
Input:
Confused about your next job?
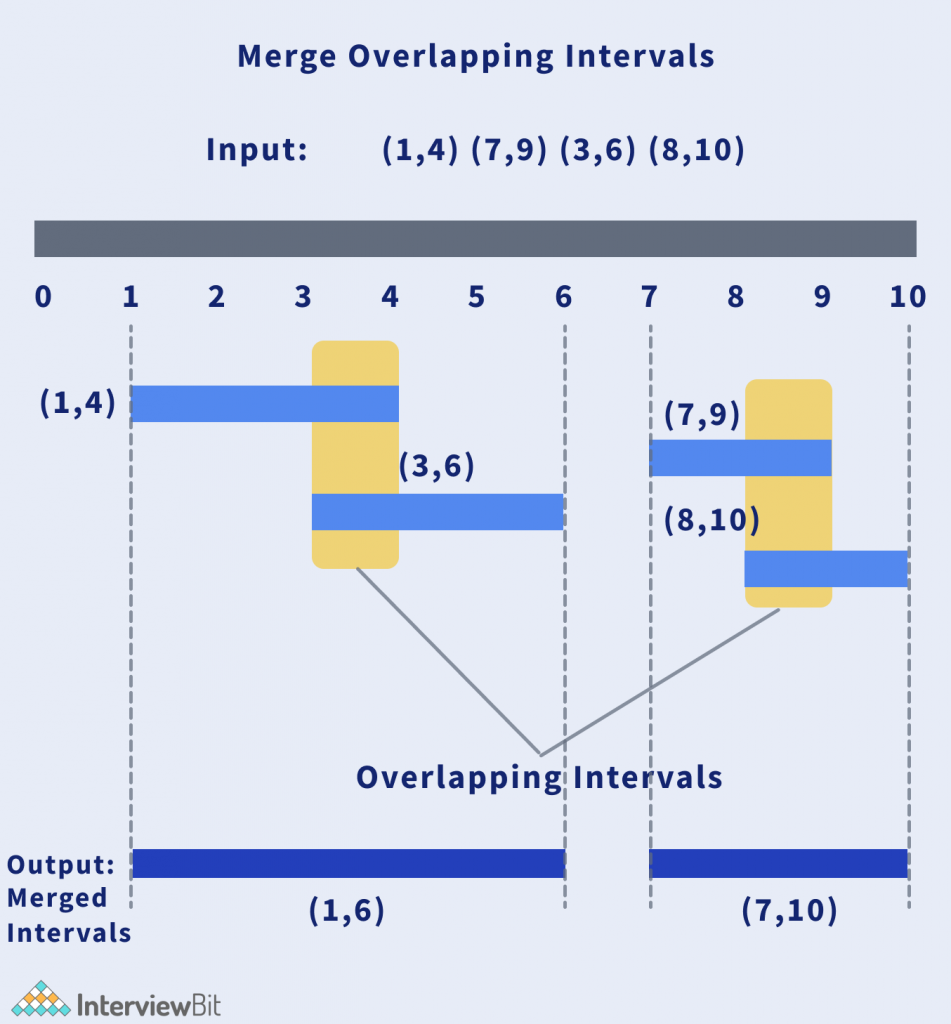
Explanation: Provided in the image
Input: intervals[] = {[1, 3],[2, 6],[8, 10],[15, 18]}
Output: {[1,6],[8,10],[15,18]}
Approach 1: Brute Force
First of all, let us try to understand the different types of intervals possible.
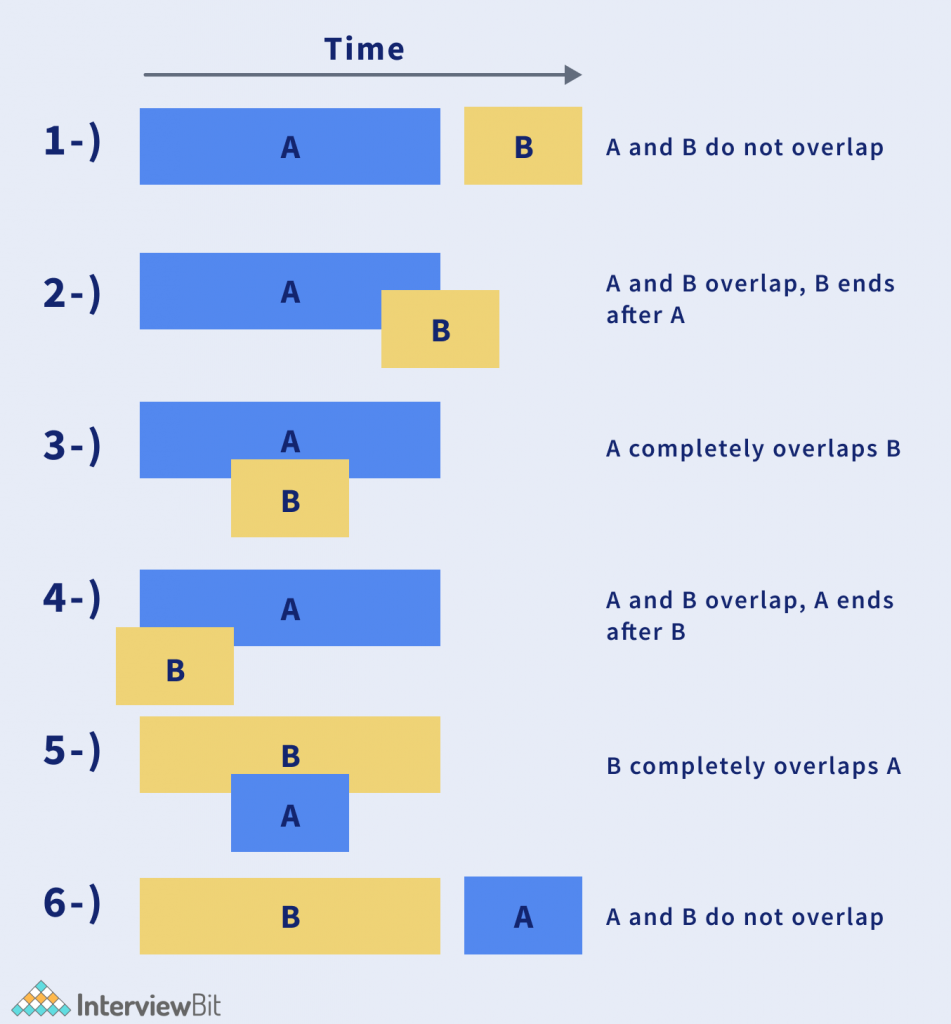
The idea is to try to mark each interval as non-visited and for each intervals which is marked as non-visited, find if another interval exists, which overlaps in any form with the current interval.
If such an interval exists, merge both intervals and mark them visited.
C++ Code
bool isOverlap(int minS, int maxE, vector<int> interval)
{
if (minS > interval[1] || maxE < interval[0])
{
return false;
}
return true;
}
vector<vector<int>> mergeIntervals(vector<vector<int>> &intervals)
{
int n = intervals.size();
vector<vector<int>> res;
vector<bool> vis(n, false);
for (int i = 0; i < n; i++)
{
if (vis[i])
{
continue;
}
vis[i] = true;
int minS = intervals[i][0];
int maxE = intervals[i][1];
while (true)
{
int cnt = 0;
for (int j = 0; j < n; j++)
{
if (!vis[j] && isOverlap(minS, maxE, intervals[j]))
{
vis[j] = true;
minS = min(minS, intervals[j][0]);
maxE = max(maxE, intervals[j][1]);
cnt++;
}
}
if (cnt == 0)
{
break;
}
}
vector<int> interval = {minS, maxE};
res.push_back(interval);
}
sort(res.begin(), res.end());
return res;
}Java Code
public static List < Interval > mergeIntervals(Interval[] intervals) {
int n = intervals.length;
List < Interval > res = new ArrayList();
boolean vis[] = new boolean[n];
for (int i = 0; i < n; i++) {
if (vis[i]) {
continue;
}
vis[i] = true;
int minS = intervals[i].start;
int maxE = intervals[i].finish;
while (true) {
int c = 0;
for (int j = 0; j < n; j++) {
if (!vis[j] && isOverlap(minS, maxE, intervals[j])) {
vis[j] = true;
minS = Math.min(minS, intervals[j].start);
maxE = Math.max(maxE, intervals[j].finish);
c++;
}
}
if (c == 0) {
break;
}
}
res.add(new Interval(minS, maxE));
}
Collections.sort(res, new Comparator < Interval > () {
public int compare(Interval a, Interval b) {
if (a.start == b.start) {
return a.finish - b.finish;
}
return a.start - b.start;
}
});
return res;
}
public static boolean isOverlap(int minS, int maxE, Interval i) {
if (minS > i.finish || maxE < i.start) {
return false;
}
return true;
}Python Code
def isOverlap(minS, maxE, i):
if minS > i.end or maxE < i.start:
return False
return True
def mergeIntervals(intervals):
n = len(intervals)
res = []
vis = [False for i in range(n)]
for i in range(n):
if vis[i] is True:
continue
vis[i] = True
minS = intervals[i].start
maxE = intervals[i].end
while 1:
cnt = 0
for j in range(n):
if vis[j] is False and isOverlap(minS, maxE, intervals[j]):
vis[j] = True
minS = min(minS, intervals[j].start)
maxE = max(maxE, intervals[j].end)
cnt += 1
if cnt == 0:
break
a = Solution(minS, maxE)
res.append(a)
return res- Time Complexity: O(N^2), where N is the total size of the interval array
- Space Complexity: O(N), as visiting array is used.
Approach 2: Sorting
Since we need to merge all the possible intervals, instead of finding if an unvisited interval exists that overlaps the current interval, the intervals can be simply sorted according to their starting time.
This ensures that all the intervals are arranged in a contagious fashion.
Let us understand this with an example :

Algorithm:
- Sort the intervals array according to startTime.
- Create an array to store the merged intervals.
- If the current and previous intervals does not overlap each other, append the current interval to the merged array.
- Else, merge both previous and current intervals and insert it into the merged array.
C++ Code
vector < vector < int >> merge(vector < vector < int >> & intervals) {
sort(intervals.begin(), intervals.end());
vector < vector < int >> merged;
for (auto interval: intervals) {
if (merged.empty() || merged.back()[1] < interval[0]) {
merged.push_back(interval);
} else {
merged.back()[1] = max(merged.back()[1], interval[1]);
}
}
return merged;
}Java Code
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
LinkedList<int[]> merged = new LinkedList<>();
for (int[] interval : intervals) {
if (merged.isEmpty() || merged.getLast()[1] < interval[0]) {
merged.add(interval);
}
else {
merged.getLast()[1] = Math.max(merged.getLast()[1], interval[1]);
}
}
return merged.toArray(new int[merged.size()][]);
}Python Code
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort(key=lambda x: x[0])
merged = []
for interval in intervals:
if not merged or merged[-1][1] < interval[0]:
merged.append(interval)
else:
merged[-1][1] = max(merged[-1][1], interval[1])
return merged- Time Complexity: O(NlogN), where N is the total size of the array
- Space Complexity: O(N), where N is the total size of the merged array
Practice Questions:
FAQ
Q.1: What is the advantage of sorting the input array according to start time?
Ans: Sorting the input array according to start time ensures that all the intervals are in a contagious manner, and helps in merging without having to search for the whole array again.
Q.2: How are the intervals merged?
Ans: The intervals are merged based on their start time and end time.
Let us consider two intervals [a, b] and [x, y]
Both the intervals overlap, if and only if: b >= x