Strassen’s Matrix Multiplication

Problem Statement

Why Strassen’s matrix algorithm is better than normal matrix multiplication and How to multiply two matrices using Strassen’s matrix multiplication algorithm?

So the main idea is to use the divide and conquer technique in this algorithm – divide matrix A & matrix B into 8 submatrices and then recursively compute the submatrices of C.

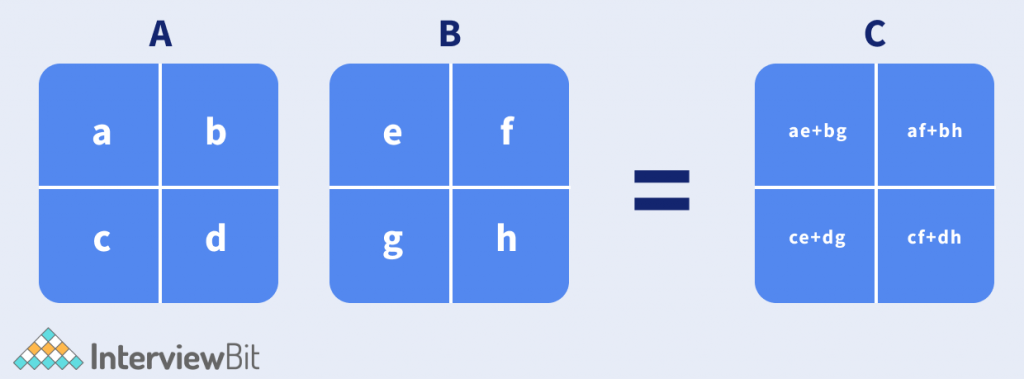
Consider the following matrices A and B:

A = |a b|,  B = |e f| and we know A*B = matrix C = |ae+bg af+bh| 
    |c d|       |g h|                              |ce+dg cf+dh|

There will be 8 recursive calls:

a * e
b * g
a * f
b * h
c * e
d * g
c * f
d * h

The above strategy is the basic O(N^3) strategy

Using the Master Theorem with T(n) = 8T(n/2) + O(n^2) we still get a runtime of O(n^3).

But Strassen came up with a solution where we don’t need 8 recursive calls but can be done in only 7 calls and some extra addition and subtraction operations.

Strassen’s 7 calls are as follows:

a * (f - h)
(a + b) * h
(c + d) * e
d * (g - e)
(a + d) * (e + h)
(b - d) * (g + h)
(a - c) * (e + f)

Our new matrix C’s new quadrants

matrix C = |p5+p4-p2+p6    p1+p2   |
           |   p3+p4    p1+p5-p3-p7| 

Approach: Strassen’s Submatrix

p5+p4-p2+p6 = (a+d)*(e+h) + d*(g-e) - (a+b)*h + (b-d)*(g+h)
            = (ae+de+ah+dh) + (dg-de) - (ah+bh) + (bg-dg+bh-dh)
            = ae+bg
 p1+p2 = a*(f-h) + (a+b)*h
       = (af-ah) + (ah+bh)
       = af+bh
 p3+p4 = (c+d)*e + d*(g-e)
       = (ce+de) + (dg-de)
       = ce+dg 
 p1+p5-p3-p7 = a*(f-h) + (a+d)*(e+h) - (c+d)*e - (a-c)*(e+f)
             = (af-ah) + (ae+de+ah+dh) -(ce+de) - (ae-ce+af-cf)
             = cf+dh

The time complexity using the Master Theorem.

T(n) = 7T(n/2) + O(n^2) = O(n^log(7)) runtime.

Approximately O(n^2.8074) which is better than O(n^3)

Pseudocode of Strassen’s multiplication

• Divide matrix A and matrix B in 4 sub-matrices of size N/2 x N/2 as shown in the above diagram.
• Calculate the 7 matrix multiplications recursively.
• Compute the submatrices of C.
• Combine these submatrices into our new matrix C

Complexity:

• Worst case time complexity: Θ(n^2.8074)
• Best case time complexity: Θ(1)
• Space complexity: Θ(logn)

C++ Code Implementation

Java Code Implementation

Python Code Implementation

Applications

Generally, Strassen’s Method is not preferred for practical applications for the following reasons.

• The constants used in Strassen’s method are high and for a typical application Naive method works better.
• For Sparse matrices, there are better methods especially designed for them.
• The submatrices in recursion take extra space.
• Because of the limited precision of computer arithmetic on noninteger values, larger errors accumulate in Strassen’s algorithm than in Naive Method