Problem Statement
We are given two sorted arrays, our task is to merge two sorted arrays in a sorted manner.
Example 1:
- Input: vec1[] = { 1, 3, 4, 5}, vec2[] = {2, 4, 6, 8}
- Output: vec3[] = {1, 2, 3, 4, 4, 5, 6, 8}
Example 2:
Confused about your next job?
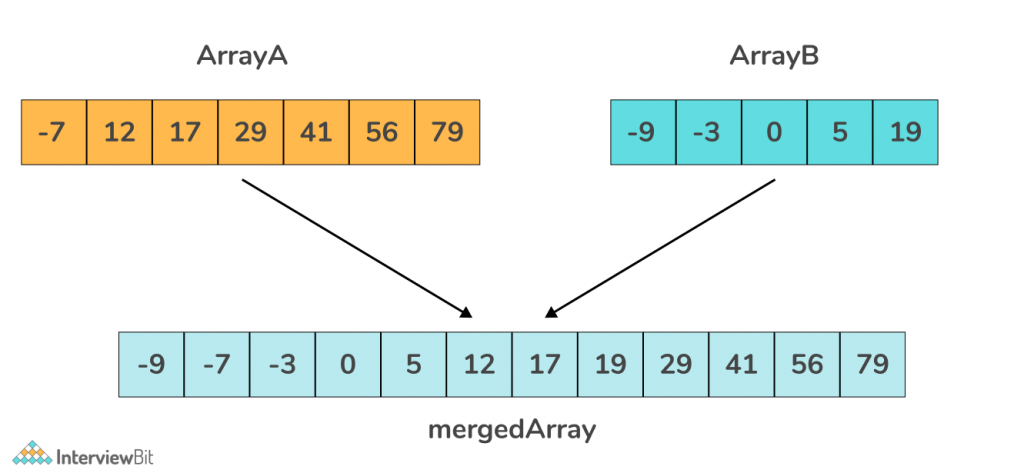
- Input : vec1[]= {-7,12,17,29,41,56,79} , vec2[]= {-9,-3,0,5,19}
- Output: {-9,-7,-3,0,5,12,17,19,29,41,56,79}
Explanation: If we merge both arrays in a sorted fashion then the resultant array will be sorted array as above.
Method 1
INTUITION: We can see the given arrays are sorted. Now our target is to make a sorted array by merging both the arrays so if we will put the smallest element always in the front of the final array then we can make our sorted array. So to choose which element is smaller we can just simply compare the front elements of both arrays.
Algorithm
- Create an array vec3[] of size n1 + n2.
- Simultaneously traverse vec1[] and vec2[].
- Pick a smaller of the current elements in vec1[] and vec2[], copy this smaller element to the next position in vec3[] and move ahead in vec3[] and the array whose element is picked.
- If there are remaining elements in vec1[] or vec2[], copy them also in vec3[].
C++ Code Implementation
void mergeArrays(int vec1[], int vec2[], int n1,
int n2, int vec3[]) {
int i = 0, j = 0, k = 0;
while (i < n1 && j < n2) {
if (vec1[i] < vec2[j])
vec3[k++] = vec1[i++];
else
vec3[k++] = vec2[j++];
}
while (i < n1)
vec3[k++] = vec1[i++];
while (j < n2)
vec3[k++] = vec2[j++];
}Java Code Implementation
public static void mergeArrays(int[] vec1, int[] vec2, int n1,
int n2, int[] vec3) {
int i = 0, j = 0, k = 0;
while (i < n1 && j < n2) {
if (vec1[i] < vec2[j])
vec3[k++] = vec1[i++];
else
vec3[k++] = vec2[j++];
}
while (i < n1)
vec3[k++] = vec1[i++];
while (j < n2)
vec3[k++] = vec2[j++];
}Python Code Implementation
def mergeArrays(vec1, vec2, n1, n2):
vec3 = [None] * (n1 + n2)
i = 0
j = 0
k = 0
while i < n1 and j < n2:
if vec1[i] < vec2[j]:
vec3[k] = vec1[i]
k = k + 1
i = i + 1
else:
vec3[k] = vec2[j]
k = k + 1
j = j + 1
while i < n1:
vec3[k] = vec1[i];
k = k + 1
i = i + 1
while j < n2:
vec3[k] = vec2[j];
k = k + 1
j = j + 1Time Complexity: O(n1 * n2) where n1 and n2 are the sizes of two arrays.
Space Complexity: O(n1+n2) where n1 and n2 are the sizes of two arrays.
Merging Without Using Extra Space
While iterating over the two sorted arrays parallelly, if we encounter the jth second array element being smaller than ith first array element, then the jth element is to be included and replace some kth element in the first array.
Algorithm
- Initialize i,j,k as 0,0,n-1 where n is the size of vec1
- Iterate through every element of vec1 and vec2 using two pointers i and j respectively
if vec1[i] is less than vec2[j]
increment i
else
swap the vec2[j] and vec1[k]
increment j and decrement k
- Sort both vec1 and vec2.
C++ Code Implementation
void merge(int vec1[], int vec2[], int n, int m) {
int i = 0, j = 0, k = n - 1;
while (i <= k && j < m) {
if (vec1[i] < vec2[j])
i++;
else {
swap(vec2[j++], vec1[k--]);
}
}
sort(vec1, vec1 + n);
sort(vec2, vec2 + m);
}Java Code Implementation
static void merge(int m, int n)
{
int i = 0, j = 0, k = n - 1;
while (i <= k && j < m) {
if (vec1[i] < vec2[j])
i++;
else {
int temp = vec2[j];
vec2[j] = vec1[k];
vec1[k] = temp;
j++;
k--;
}
}
Arrays.sort(vec1);
Arrays.sort(vec2);
}Python Code Implementation
def merge(self, nums1, m, nums2, n):
while m > 0 and n > 0:
if nums1[m-1] >= nums2[n-1]:
nums1[m+n-1] = nums1[m-1]
m -= 1
else:
nums1[m+n-1] = nums2[n-1]
n -= 1
if n > 0:
nums1[:n] = nums2[:n]- Time Complexity: O((n+m)log(n+m)) where n and m are the sizes of two arrays.
- Space Complexity: O(1).
Practice Question
FAQs
Q.1: Why does merge sort require extra space?
Ans: When we are merging two arrays then for merging we need one more additional space to create the array.
Q.2: Is Quicksort faster than mergesort?
Ans: Merge sort is more efficient and works faster than quicksort in the case of a larger size array. Quicksort is more efficient and works faster than merge sort in case of the smaller size of an array.