Minimum Number of Jumps

Minimum Jumps To Reach End of an Array

Given an array of non-negative integers, A, of length N. You are initially positioned at the first index of the array. Each element in the array represents your maximum jump length at that position.

Return the minimum number of jumps required to reach the last index.

If it is not possible to reach the last index, return -1.

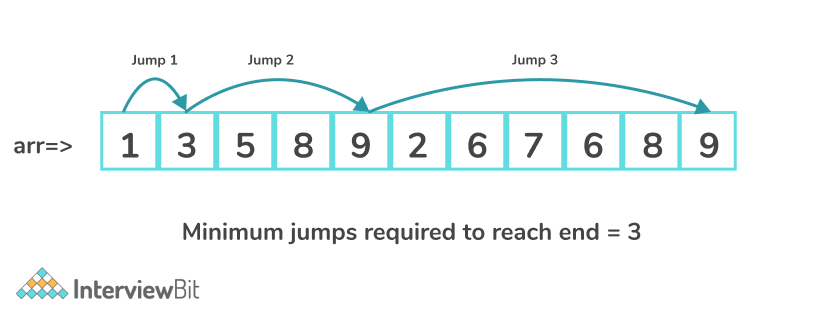
Examples:

Input: arr[] = [1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9]
Output: 3
Explanation: Provided in the above image

Input:  arr[] = [2, 3, 1, 1, 4]
Output: 2
Explanation: Travel from 2 -> 3 -> end.

Approach 1: Bruteforce(Recursive)

A simple approach to solve this problem is to start from the first element of the array and recursively travel to all elements that are reachable from that element. Similarly, recursively travel to all other elements and find the minimum jumps to reach the end of the array.

Algorithm:

• Create a recursive function that determines the minimum jumps required to reach the end of the array.
• Start from the first element of the array and recurse for each step till current step > 0.
• Minimise the value for each iteration.
• Return the minimum jumps.

C++Implementation

 
int decideJump(int nums[], int n, int currPos){
    if(currPos >=  n-1){
        return 0;
    }
    int minJump = INT_MAX;
    int maxSteps = nums[currPos]
    while(maxSteps > 0){
        minJump = min(minJump, 1 + decideJump(nums,n,currPos+maxSteps))
        maxSteps = maxSteps - 1;
    }
    return minJump
}
   
int jump(int nums[], int n) {
    return decideJump(nums, n, 0);
}

JavaImplementation

int decideJump(int[] nums, int n, int currPos){
    if(currPos >=  n-1){
        return 0
    }
    int minJump = INT_MAX
    int maxSteps = nums[currPos]
    while(maxSteps > 0){
        minJump = min(minJump, 1 + decideJump(nums,n,currPos+maxSteps))
        maxSteps = maxSteps - 1
    }
    return minJump
}
   
int jump(int[] nums, int n) {
    return decideJump(nums, n, 0)
}

PythonImplementation

def decideJump(nums, n, currPos):
    if currPos >=  n-1:
        return 0
    minJump = 9999999999999
    maxSteps = nums[currPos]
    whilemaxSteps > 0 :
        minJump = min(minJump, 1 + decideJump(nums,n,currPos+maxSteps))
        maxSteps = maxSteps - 1
    return minJump
 
   
def jump(nums, n):
    return decideJump(nums, n, 0)

Time Complexity: O(N^N), where N is the total elements in the array.
Space Complexity: O(1), since no extra space is used.

Approach 2: Dynamic Programming

In the previous approach, if you clearly observe the recursion tree, it can be clearly seen that many of the subproblems are calculated more than once, which in turn takes more time as well as space. Therefore, we can store the answer to such overlapping subproblems in a table and get the answer to this problem in O(1) using a dynamic programming approach.

Algorithm:

• Create a dp[] array of size N, where N is the size of the given array.
• Initialise all the elements of the array to INT_MAX.
• Initialise dp[0] = 0, since, we are standing at the first index and we need no jumps to reach the first element.
• The recursive structure would be:
  dp[i] = 1 + min(dp[i], 1 + min( dp[i+1], dp[i+2],. . . dp[i + dp[i] + 1]))
• Iterate a loop from 0 till N – 1. Run a nested loop from i + 1 till min(i + arr[i] + 1, n) and find the minimum of jumps[i] and i + jumps[i].
• After iterations, return the value of dp[N – 1]

C++Code For DP Method

int minJump(int num[], int n){
    int dp[n] = {INT_MAX}
    dp[0] = 0
    for(i = 0 to i < n){
        for(j = i+1 to j < min(i+num[i]+1, n)) {
            dp[j] = min(dp[j], 1 + dp[i])
        }
    }
    return dp[n-1]
}

Java Code For DP Method

int minJump(int[] num, int n){
    int[n] dp = {INT_MAX}
    dp[0] = 0
    for(i = 0 to i < n){
        for(j = i+1 to j < min(i+num[i]+1, n)) {
            dp[j] = min(dp[j], 1 + dp[i])
        }
    }
    return dp[n-1]
}

Python Code For DP Method

def minJump(num, n){
    dp = [n] * (99999999)
    dp[0] = 0
    For i in range(n):
        For j in range(i+1,  min(i+num[i]+1, n)):
            dp[j] = min(dp[j], 1 + dp[i])
    return dp[n-1]

Time Complexity: O(N^ 2), where N is the total elements in the array.
Space Complexity: O(N), since dp[] array is used.

Approach 3: Greedy Approach

In the previous approach, it was observed that if we are at position i, the maximum one can jump is (i,  i + nums[i]).

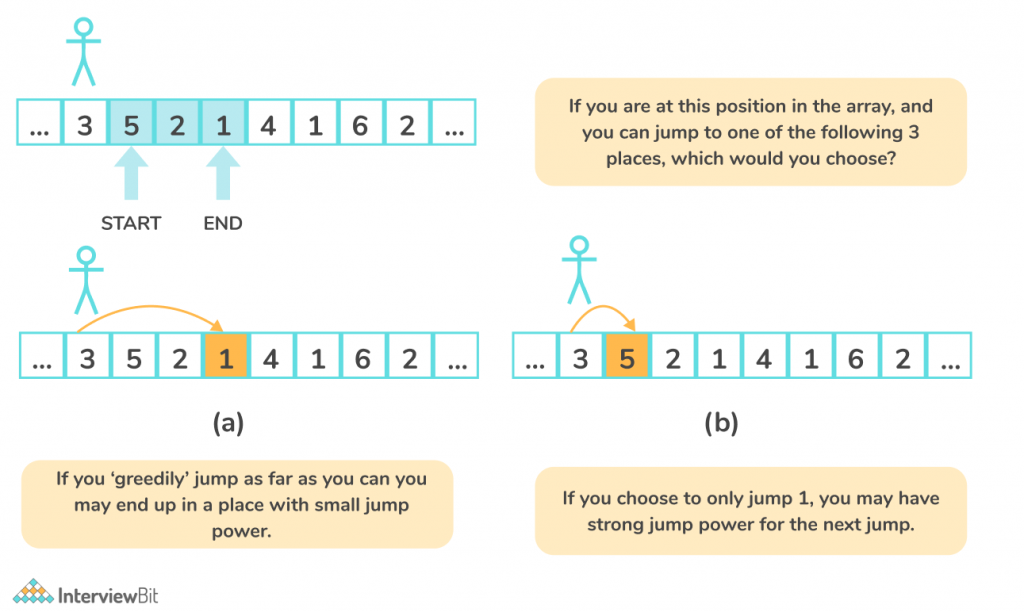
In the below example, only can jump in three different positions from the given index i.

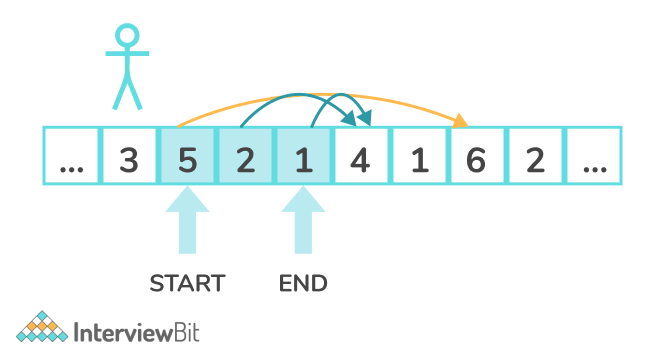
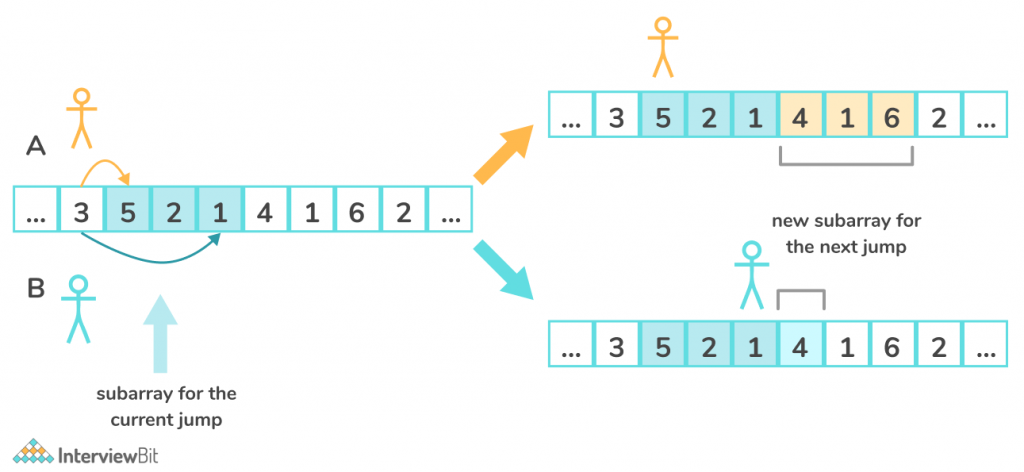
Algorithm:

• Consider three variables, jumps, which stores the number of jumps, end, which denotes the end of the array and farthest denoting the farthest one can jump and initialise them to 0.
• Traverse over the given array and perform the following operation:
  • farthest = i + nums[i]
  • If end is reached, then ith jump is finished, therefore update end = farthest.
• Return total jumps.

C++Code For Greedy Approach

int minJump(int nums[], int n) {
        int jumps = 0, currentJumpEnd = 0, farthest = 0;
        for (int i = 0; i < n - 1; i++) {
             farthest = max(farthest, i + nums[i]);
             if (i == currentJumpEnd) {
                jumps++;
                currentJumpEnd = farthest;
            }
        }
        return jumps;
    }

JavaCode For Greedy Approach

public int minJump(int[] nums) {
        int jumps = 0, currentJumpEnd = 0, farthest = 0;
        for (int i = 0; i < nums.length - 1; i++) {
             farthest = Math.max(farthest, i + nums[i]);
             if (i == currentJumpEnd) {
                jumps++;
                currentJumpEnd = farthest;
            }
        }
        return jumps;
    }

Python Code For Greedy Approach

def minJump(nums):
        jumps = 0
        current_jump_end = 0
        farthest = 0
        for i in range(len(nums) - 1):
            farthest = max(farthest, i + nums[i])
            if i == current_jump_end:
                jumps += 1
                current_jump_end = farthest
        return jumps

Time Complexity: O(N), where N is the total elements in the array.
Space Complexity: O(1), since dp[] array is used.

Practice Question

Min Jumps Array

FAQ

1. What is the most efficient approach to solve this problem?
   The greedy approach is the most efficient approach since it takes, O(N) time and O(1) space,

2. What is the recurrence relation of the dynamic programming approach?
   The recurrence relation of the dynamic programming approach is as follows –
           dp[i] = 1 + min(dp[i], 1 + min( dp[i+1], dp[i+2],. . . dp[i + dp[i] + 1]))