Problem Statement
Given an array with distinct integers, find the minimum number of swaps required to sort it.
Sample Test Cases:
Input 1:
Confused about your next job?
a = [4, 3, 2, 1]
Output 1:
2
Explanation 1:
We swap 4 with 1, and 2 with 3 requiring a minimum of 2 swaps.
Input 2:
a = [1, 5, 4, 3, 2]
Output 2:
2
Explanation 2:
We swap 5 with 2 and 4 with 3 requiring a minimum of 2 swaps.
Approach 1(Graph-Based Approach)
This problem can be solved quite easily if we change our perspective and try to model this problem into a graph problem. The n indexes in the array will act as nodes of our graph, and there will be a directed edge from node i to node j if the element at index i has its position as j in the sorted version of the array.
For the input of [4, 3, 2, 1], the graph will be as follows,
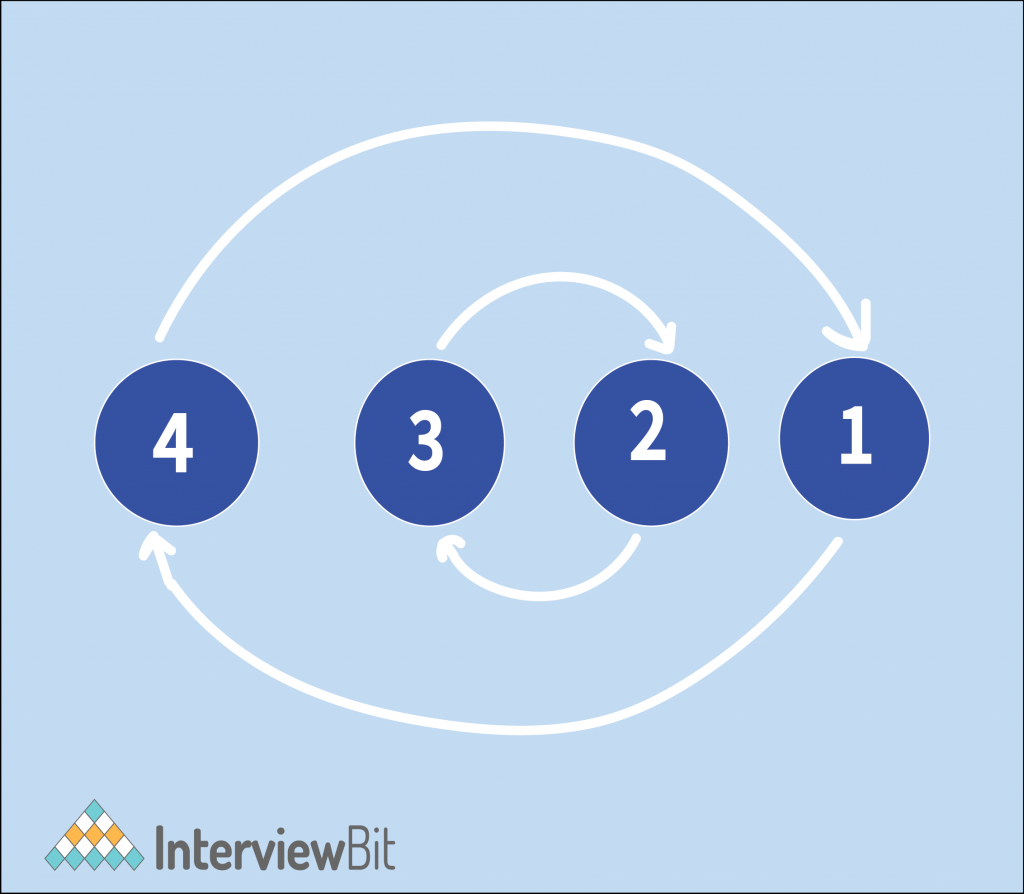
For the input of [1, 5, 4, 3, 2], the graph will be as follows,
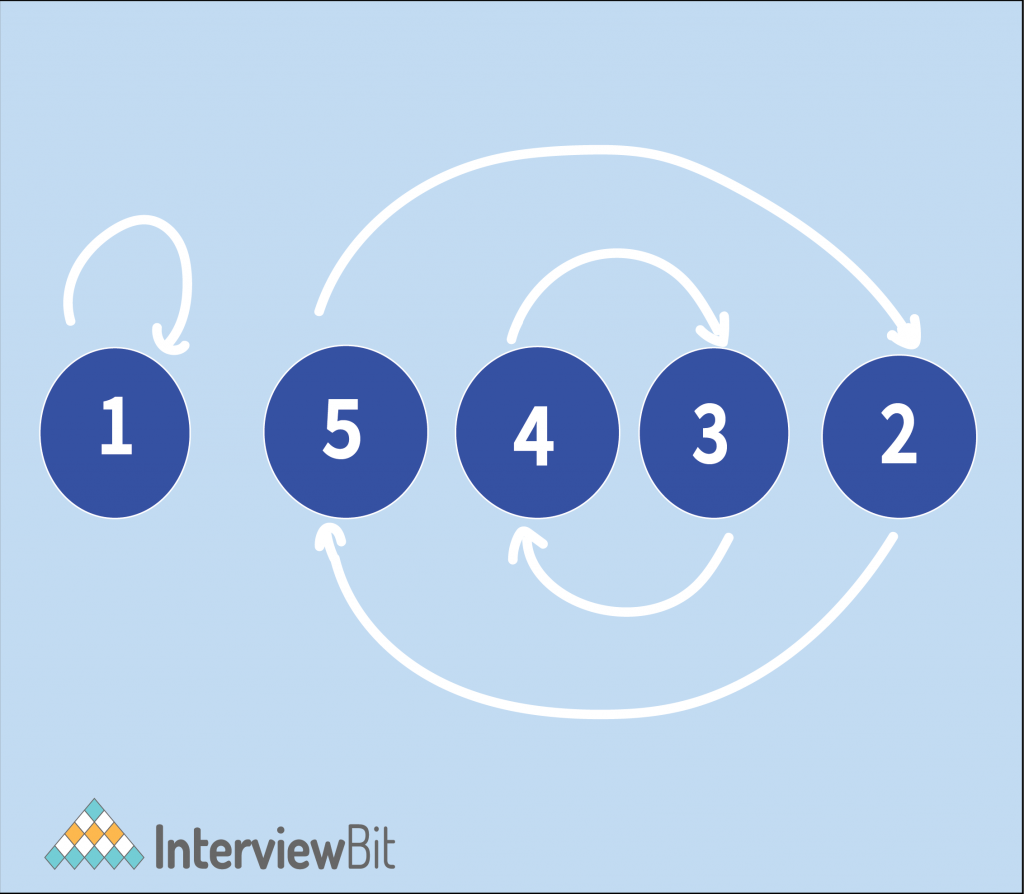
Observe that the graph is made up of many non-intersecting cycles. Note for a cycle of size 2, we need at most 1 swap to sort it, for a cycle of size 3, we need at most 2 swaps to sort it, and so on. So we can generalize that for a cycle of size n, we need at most n – 1 swaps to sort it. So, to sort the entire array, we will need to sum up (cycle size – 1) over all the cycles of the graph, which can be performed easily with a standard Depth First Search.
How to form the graph?
To form the graph, we need to know at what position will the current element go in the final array? For that the following algorithm can be used:
- Store the Pair of (elements, indexes) in a list.
- Sort the list on the basis of the first entity (elements).
- Using the indexes of the sorted list and the original list, we can add the edges for the graph.
Code / Implementation:
C++ Code
void dfs(vector < int > vec[], vector < bool > & vis, int node, int & compSize) {
vis[node] = true;
compSize += 1;
for (auto x: vec[node]) {
if (!vis[x]) {
dfs(vec, vis, x, compSize);
}
}
}
int minimumSwaps(vector < int > & a, int n) {
vector < int > vec[n + 1];
vector < pair < int, int >> aux;
for (int i = 0; i < n; i++) {
pair < int, int > p = {
a[i],
i + 1
};
aux.push_back(p);
}
sort(aux.begin(), aux.end());
for (auto x: aux) {
cout << x.first << " " << x.second << endl;
}
vector < bool > vis(n + 1, false);
for (int i = 0; i < n; i++) {
vec[aux[i].second].push_back(i + 1);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
int compSize = 0;
dfs(vec, vis, i, compSize);
ans += (compSize - 1);
}
}
return ans;
}Java Code
public class Pair < T, U > {
private final T key;
private final U value;
public Pair(T key, U value) {
this.key = key;
this.value = value;
}
public T getKey() {
return this.key;
}
public U getValue() {
return this.value;
}
}
public void dfs(ArrayList < Integer > vec[], boolean[] vis, int node, int[] compSize) {
vis[node] = true;
compSize[0] += 1;
for (int i = 0; i < vec[node].size(); i++) {
if (!vis[(int) vec[node].get(i)]) {
dfs(vec, vis, vec[node].get(i), compSize);
}
}
}
public int minimumSwaps(int[] a, int n) {
ArrayList < Pair < Integer, Integer >> aux = new ArrayList < Pair < Integer, Integer >> ();
for (int i = 0; i < n; i++) {
aux.add(new Pair < Integer, Integer > (a[i], i + 1));
}
aux.sort(new Comparator < Pair < Integer, Integer >> () {
public int compare(Pair < Integer, Integer > first, Pair < Integer, Integer > second) {
if (first.key > second.key) {
return 1;
} else if (first.key < second.key) {
return -1;
} else {
return 0;
}
}
});
boolean[] vis = new boolean[n + 1];
for (int i = 0; i <= n; i++) {
vis[i] = false;
}
ArrayList < Integer > vec[] = new ArrayList[n + 1];
for (int i = 0; i < n; i++) {
vec[i + 1] = new ArrayList < > ();
}
for (int i = 0; i < n; i++) {
vec[aux.get(i).value].add(i + 1);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
int[] compSize = new int[1];
compSize[0] = 0;
if (!vis[i]) {
dfs(vec, vis, i, compSize);
ans += (compSize[0] - 1);
}
}
return ans;
}Python Code
def dfs(vec, vis, node, compSize):
vis[node] = True
compSize[0] += 1
for x in vec[node]:
if not vis[x]:
dfs(vec, vis, x, compSize)
def minimumSwaps(a, n):
aux = [*enumerate(a)]
aux.sort(key=lambda it: it[1])
vis = [False] * (n + 1)
vec = [[] for i in range(n + 1)]
for i in range(n):
vec[aux[i][0] + 1].append(i + 1)
ans = 0
for i in range(1, n + 1):
compSize = [0]
if not vis[i]:
dfs(vec, vis, i, compSize)
ans += compSize[0] - 1
return ansComplexity Analysis:
- Time Complexity: O(n * logn)
- Space Complexity: O(n)
Approach 2(Observation Based)
A simple approach can also be used to solve this problem since it tells us that the array elements are distinct. We can compress the array into numbers from 1 to n, using the same sorting-based approach we used in the previous algorithm. However, this time, instead of forming the graph, we can simply swap an element with the element where it ought to be in the sorted array, whenever we find it out of position, and count the number of swaps needed. It can be proved that the algorithm takes at the maximum upper bound of O(n) moves to terminate and sort the array completely.
Proof that the algorithm terminates with at max of O(n) moves:
Observe that each swap operation puts at least one element into its proper position in the array. Since the total number of elements in the array is bounded by n, the number of swap operations required to sort the array must also be bounded by n.
Implementation:
C++ Code
int minimumSwaps(vector < int > & a, int n) {
map < int, int > m;
vector < int > copy = a;
sort(copy.begin(), copy.end());
for (int i = 0; i < n; i++) {
m[copy[i]] = i + 1;
}
int moves = 0;
for (int i = 0; i < n; i++) {
if (i + 1 != m[a[i]]) {
swap(a[i], a[m[a[i]] - 1]);
moves++;
}
}
return moves;
}Java Code
public static int minimumSwaps(int[] a, int n) {
HashMap < Integer, Integer > m = new HashMap < Integer, Integer > ();
int[] copy = new int[n];
for (int i = 0; i < n; i++) {
copy[i] = a[i];
}
Arrays.sort(copy);
for (int i = 0; i < n; i++) {
m.put(copy[i], i + 1);
}
int moves = 0;
for (int i = 0; i < n; i++) {
if ((i + 1) != (int) m.get(a[i])) {
int temp = a[i];
int pos = m.get(a[i]) - 1;
a[i] = a[pos];
a[pos] = temp;
moves++;
}
}
return moves;
}Python Code
def minimumSwaps(a, n):
copy = a.copy()
copy.sort()
m = {}
for i in range(n):
m[copy[i]] = i + 1
moves = 0
for i in range(n):
if (i + 1) != m[a[i]]:
temp = a[i]
pos = m[a[i] - 1]
a[i] = a[pos]
a[pos] = temp
moves += 1
return movesComplexity Analysis:
- Time Complexity: O(n * logn) // Due to Sorting
- Space Complexity: O(n)
FAQs
1. Can the complexity of the algorithm be improved if the array was a permutation?
A. The complexity of the 2nd approach can be improved to O(n) if the array was a permutation.
2. What algorithm is used to sort the array?
A. Although there is a variety of sorting algorithms available, merge sort is used here to sort the array as it provides one of the best worst-case asymptotics among all sorting algorithms.