Preorder Traversal

Problem Statement

Given a binary tree, the task is to print the preorder traversal of the tree.

Pre-Order is a way to traverse the binary tree in which our directions are fixed

i.e. root-> left – > right. It means first we will traverse the root of the tree and then go to its left subtree and after traversing that subtree we will move to its right part of the subtree.

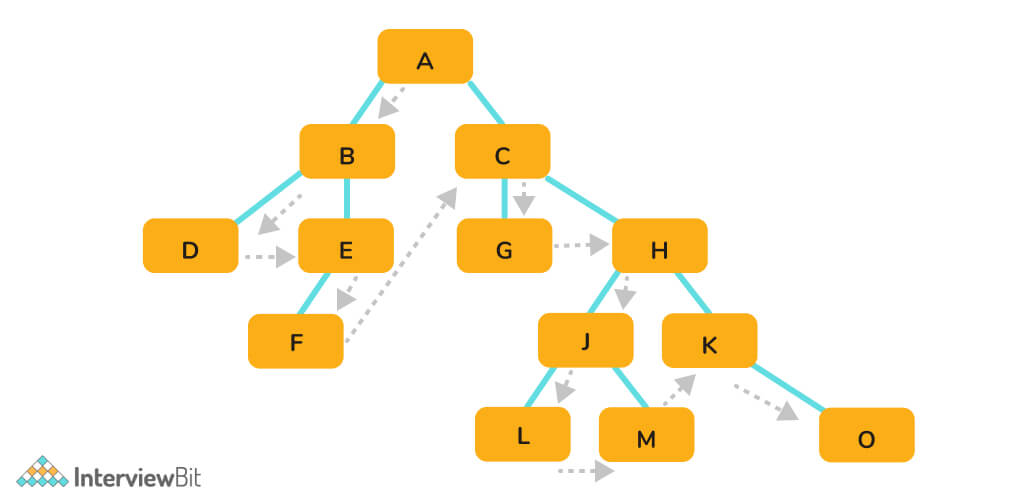
Example:

• Input: [A,B,C,D,E,F,G,NULL,NULL,NULL,NULL]
• Output: [A,B,DE,C,F,G]

Explanation:

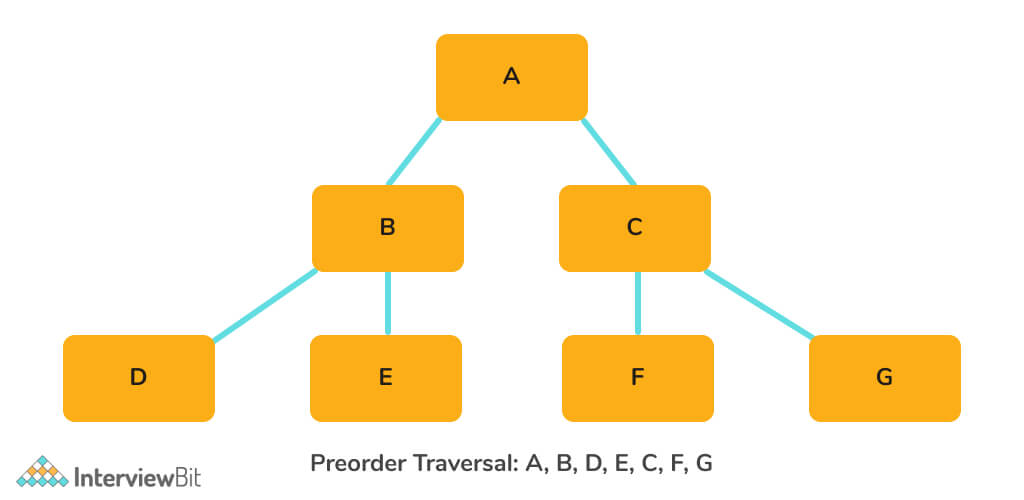
• Input: [1,2,3,4,5,6,7,-1,-1,-1,-1]
• Output: [1,2,4,5,3,6,7]

1. Recursive Approach

For implementing a recursive approach we first call the root of the current tree and then traverse the left and right subtree.

Implementation of Recursive Approach

C++ Implementation

void printPreorder(struct Node* node)
{
    if (node == NULL)
        return;
 
    /* first print data of node */
    cout << node->data << " ";
 
    /* then recur on left subtree */
    printPreorder(node->left);
 
    /* now recur on right subtree */
    printPreorder(node->right);
}

Java Implementation

public List < Integer > preorderTraversal(TreeNode root) {
  List < Integer > pre = new LinkedList < Integer > ();
  if (root == null) return pre;
  pre.add(root.val);
  pre.addAll(preorderTraversal(root.left));
  pre.addAll(preorderTraversal(root.right));
  return pre;
}

Python Implementation

def printPreorder(root):
 
    if root:
 
        # First print the data of node
        print(root.val),
 
        # Then recur on left child
        printPreorder(root.left)
 
        # Finally recur on right child
        printPreorder(root.right)

• Time complexity: O(N), Where N is the size of the binary tree.
• Space complexity: O(1) If we don’t consider the function call stack, else O(h), h is the height of the tree.

2. Iterative Approach

The iterative approach uses stack data structure to print the preorder traversal. Follow the below steps.

• Create an empty stack, Push the root node to the stack.
• Do the following while the stack is not empty.
• Pop an item from the stack and print it.
• Push the right child of the popped item to stack.
• Push the left child of the popped item to stack.

Implementation of Iterative Approach

C++ Implementation of Iterative Approach

vector < int > preorderTraversal(TreeNode * root) {
  stack < TreeNode * > nodeStack;
  vector < int > result;
  //base case
  if (root == NULL)
    return result;
  nodeStack.push(root);
  while (!nodeStack.empty()) {
    TreeNode * node = nodeStack.top();
    result.push_back(node -> val);
    nodeStack.pop();
    if (node -> right)
      nodeStack.push(node -> right);
    if (node -> left)
      nodeStack.push(node -> left);
  }
  return result;

}

Java Implementation of Iterative Approach

public List < Integer > preorderTraversal(TreeNode node) {
  List < Integer > list = new LinkedList < Integer > ();
  Stack < TreeNode > rights = new Stack < TreeNode > ();
  while (node != null) {
    list.add(node.val);
    if (node.right != null) {
      rights.push(node.right);
    }
    node = node.left;
    if (node == null && !rights.isEmpty()) {
      node = rights.pop();
    }
  }
  return list;
}

Python Implementation of Iterative Approach

def preorderTraversal(self, root):
    ret = []
    stack = [root]
    while stack:
        node = stack.pop()
        if node:
            ret.append(node.val)
            stack.append(node.right)
            stack.append(node.left)
    return ret

• Time complexity: O(N), Where N is the size of the binary tree.
• Space complexity: O(N)

Practice Questions

Preorder Traversal
Valid BST from Preorder

Frequently Asked Questions

Q.1: Is there any way to print the preorder traversal in O(1) space (Including function call stack)?

Ans: Yes, using Morris traversal.

Q.2: Can we write preorder traversal from Inorder and Postorder traversal?

Ans: Yes.

Q.3: Is Preorder sufficient to maintain the structure of the tree?

Ans: No, we need a Preorder and Inorder to find a unique structure.