Longest Common Subsequence

Problem Statement

Given two strings, the task is to find the longest common subsequence present in the given strings in the same order.

The subsequence of a given sequence is a sequence that can be derived from the given sequence by deleting some or no elements without changing the order of the remaining elements.

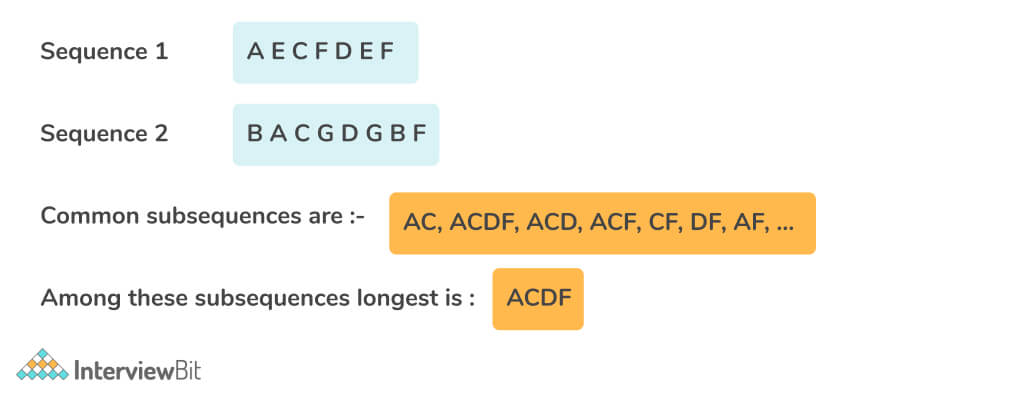
Example:

• Input s1: “abcde”
• s2: “ace”
• Output: 3

Explanation: Subsequence “ace” of length 3 is the longest.

• Input s1: “ezupkr”
• s2: “ubmrapg”
• Output: 2

Explanation: Subsequence “ur” of length 2 is the longest.

1. Simple Approach Solution

The simple approach checks for every subsequence of sequence 1 whether it is also a subsequence in sequence 2.

Sequence S1 and S2 with length n and m respectively. So, the lcs of S1 and S2 is the maximum of LCS( S1[1…m-1],S2[1….n]),LCS(S1[1…m],S2[1…..n-1])).

• So, the parameters needed are the two sequences and two iterators (S1, S2,i,j) for the sequences
• The base case will be if any of the lengths is not valid (i.e less or equal to zero) then return
• Check for the current element of both iterators if equal then include that in LCS and make a recursive call for the prev element in both sequences (i.e. i-1,j-1).
• If both iterator elements are not equal then LCS can be obtained by including any of the current elements. So making both calls and taking the maximum of those
  • Including S1’s recursive call will be LCS(S1,S2,i,j-1) [ i is for S1 and j is for S2]
  • Including S2’s recursive call will be LCS(S1,S2,i-1,j)

Printing Longest Common Subsequence

C++ Implementation

// Finding Length of longest common subsequence
// iterating from last character so i and j are the length of strings initially
int LCS(string X, string Y, int i, int j) {
  if (i == 0 || j == 0) {
    return 0;
  }

  if (X[m - 1] == Y[n - 1]) {
    return LCS(X, Y, i - 1, j - 1) + 1;
  }

  return max(LCS(X, Y, i, j - 1), LCS(X, Y, i - 1, j));
}

Java Implementation

public static int LCS(String X, String Y, int i, int j) {
  if (i == 0 || j == 0) {
    return 0;
  }

  if (X.charAt(i - 1) == Y.charAt(j - 1)) {
    return LCS(X, Y, i - 1, j - 1) + 1;
  }

  return Integer.max(LCS(X, Y, i, j - 1),
    LCS(X, Y, i - 1, j));
}

Python Implementation

# sequences `S1[0...m-1]` and `Y[0...n-1]`
def LCS(X, Y, m, n):
 
    # return if the end of either sequence is reached
    if m == 0 or n == 0:
        return 0
 
    if X[i - 1] == Y[j - 1]:
        return LCS(X, Y, i - 1, j - 1) + 1
 
    return max(LCS(X, Y, i, j - 1), LCS(X, Y, i- 1, j))

Recursive Tree for Example 1

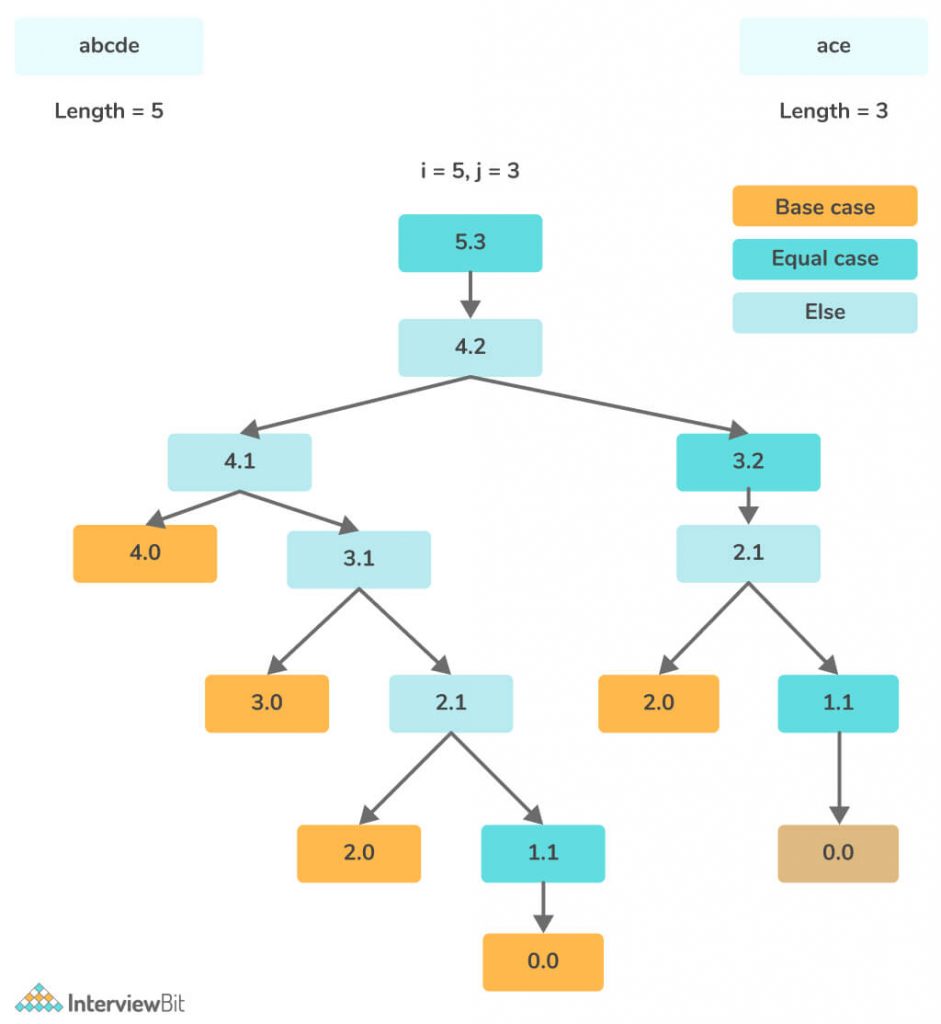
So total subsequence possible is 2^n for a sequence of length n

• Time complexity: O(2^(n+m)), Where n and m are lengths of sequences.
• Space complexity: O(1)

2. Dynamic Programming Approach

• We can see in our recursive tree that many of the sub-problems are overlapping and it would be very much increased as the tree size increases and it would compute for the same problem again.
• Using dynamic programming we can compute a problem and store the optimal result and use it further avoiding repeated execution.
• DP[i][j] state: longest sequence using starting I characters of string S1 and starting j characters of string S2.

Implementation of the DP Approach

C++ Implementation of DP Approach

// dp[][] Initialized with -1
int dp[N][M];
int LCS(string X, string Y, int i, int j) {
  if (i == 0 || j == 0) {
    return 0;
  }
  // Here we are checking if this problem has been computed earlier 
  if (dp[i][j] != -1)
    return dp[i][j];
  if (X[m - 1] == Y[n - 1]) {
    return dp[i][j] = LCS(X, Y, i - 1, j - 1) + 1;
  }
  // computing and storing the problem in dp
  return dp[i][j] = max(LCS(X, Y, i, j - 1), LCS(X, Y, i - 1, j));
}

Java Implementation of DP Approach

public static int LCS(String X, String Y, int i, int j, Map < String, Integer > dp) {
  if (i == 0 || j == 0) {
    return 0;
  }
  String key = i + "|" + j;
  if (!dp.containsKey(key)) {
    if (X.charAt(i - 1) == Y.charAt(j - 1)) {
      dp.put(key, LCS(X, Y, i - 1, j - 1, dp) + 1);
    } else
      dp.put(key, Integer.max(LCS(X, Y, i, j - 1, dp),
        LCS(X, Y, i - 1, j, dp)));
  }
  return dp.get(key);
}

Python Implementation of DP Approach

def LCSLength(X, Y, i, j, dp={}):

    if i == 0 or j == 0:
        return 0
    key = (i, j)
    if key not in dp:

        if X[i - 1] == Y[j - 1]:
            dp[key] = LCSLength(X, Y, i - 1, j - 1, dp) + 1

        else:
            dp[key] = max(LCSLength(X, Y, i, j - 1, dp), LCSLength(X, Y, i - 1, j, dp))

    return dp[key]

• Time complexity: O(nm), Where n and m are the lengths of sequences.
• Space complexity: O(nm)

3. Bottom-Up Technique

It’s a bottom-up technique in which we compute the smaller values of the problem and compute larger ones from them. It’s more efficient w.r.t time complexity as it doesn’t use the recursive stack and is hence more efficient.

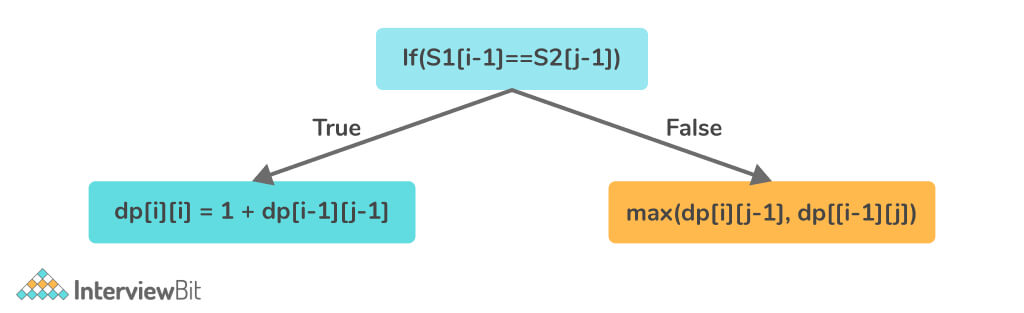
Implementation

C++ Implementation of Bottom-Up Technique

int LCS(string a, string b) {
    int m = a.length(), n = b.length();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (a[i - 1] == b[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m][n];
}

Java Implementation of Bottom-Up Technique

public int LCS_iterative(String X, String Y) {
  int dp[][] = new int[Y.length() + 1][X.length() + 1];
  char[] s1 = X.toCharArray();
  char[] s2 = Y.toCharArray();

  for (int i = 1; i <= s2.length; i++) {
    for (int j = 1; j <= s1.length; j++) {
      if (s2[i - 1] == s1[j - 1]) {
        dp[i][j] = 1 + dp[i - 1][j - 1];
      } else {
        dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
      }
    }
  }
  return dp[s2.length][s1.length];
}

Python Implementation of Bottom-Up Technique

def solve(self, X, Y):
    # Initializing X dp array of size
    n = len(X)
    m = len(Y)
    dp = [[0 for i in range(m + 1)] for i in range(n + 1)]

    for i in range(n - 1, -1, -1):
        for j in range(m - 1, -1, -1):
            if X[i] == Y[j]:
                dp[i][j] = dp[i + 1][j + 1] + 1
            else:
                dp[i][j] = max(dp[i + 1][j], dp[i][j + 1])
    return dp[0][0]

• Time complexity: O(nm), Where n and m are the lengths of sequences.
• Space complexity: O(nm)

Practice Question

Longest Common Subsequency

Frequently Asked Questions

Q.1: How do you find the longest common subsequence?

Ans: The most efficient method is to use the dynamic programming approach of storing sub-problems.

Q.2: What is the time complexity of the longest common subsequence?

Ans: It depends if we don’t use dynamic programming to store subproblems then it would be O(2^(n+m)) time and O(1) space and using dynamic programming its O(nm) time and O(nm) space where n,m are lengths of sequence.

Q.3: Is the longest common subsequence NP-complete?

Ans: The 2D-LCS problem is NP-hard.

Proof: We prove the hardness of the problem by a reduction from the Clique problem.