Remove Loop in Linked List

Problem Statement

Given a linked list. If the linked list contains a loop, return True and remove the loop.
A linked list contains a cycle if it consists of a node that can be reached again by continuously following the next pointer.

Examples:
Input:

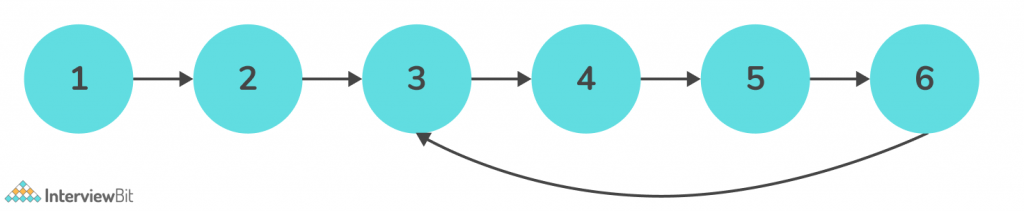
Output: 1 -> 2 -> 3 -> 4 -> 5
Explanation: The linked list consists of a loop, where the last node connects to the second node. Hence, remove the loop

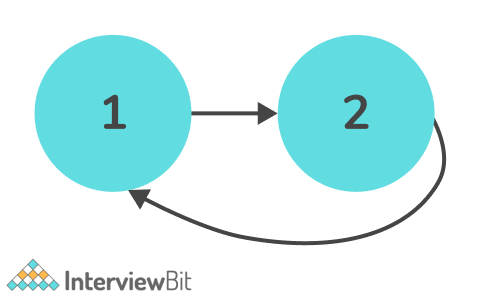
Output: 1 -> 2

Approach: Using HashSet

The most straightforward approach to solve this problem is to check whether a node in the linked list has been visited before. To perform this operation, a hashmap can be used. If a node has already occurred before, simply set the current pointer to NULL.

Algorithm

• Initialise a hashmap.
• Traverse the linked list till the head pointer isn’t NULL:
  • If the current node is already present in the hashmap, it ensures that the linked list contains a loop. Hence, set the node to NULL.
  • Else, continue traversing and continue inserting the node into the HashSet.
• If no node satisfies the above conditions, then the linked list does not contain any cycle.

C++ Implementation

void hashAndRemove(Node * head) {
  unordered_map < Node * , int > node_map;
  Node * last = NULL;
  while (head != NULL) {
    if (node_map.find(head) == node_map.end()) {
      node_map[head]++;
      last = head;
      head = head -> next;
    } else {
      last -> next = NULL;
      break;
    }
  }
}

Java Implementation

 static boolean removeLoop(Node h)
    {
        HashSet<Node> s = new HashSet<Node>();
        Node prev = null;
        while (h != null) {
            if (s.contains(h)) {
                prev.next = null;
                return true;
            }
            else {
                s.add(h);
                prev = h;
                h = h.next;
            }
        }
 
        return false;
    }

Python Implementation

def removeLoop(head):
        mp = set()
        prev = NULL
        while head is not None:
            if head in mp:
                prev.next = NULL
                return True
            else:
                mp.add(head)
                prev = head
                head = head.next
        return False

• Time Complexity: O(N) where N is the number of nodes of the linked list.
• Space Complexity:O(N), as HashSet is used

Efficient Approach: Using Floyd’s Cycle Detection Algorithm

This approach uses a two-pointer – a fast pointer and a slow pointer to determine if there exists a cycle in the loop. The slow pointer moves one node ahead at a time, while the fast pointer moves two nodes ahead at a time.

If a loop exists in the linked list, the fast and slow pointers are bound to meet at some point.

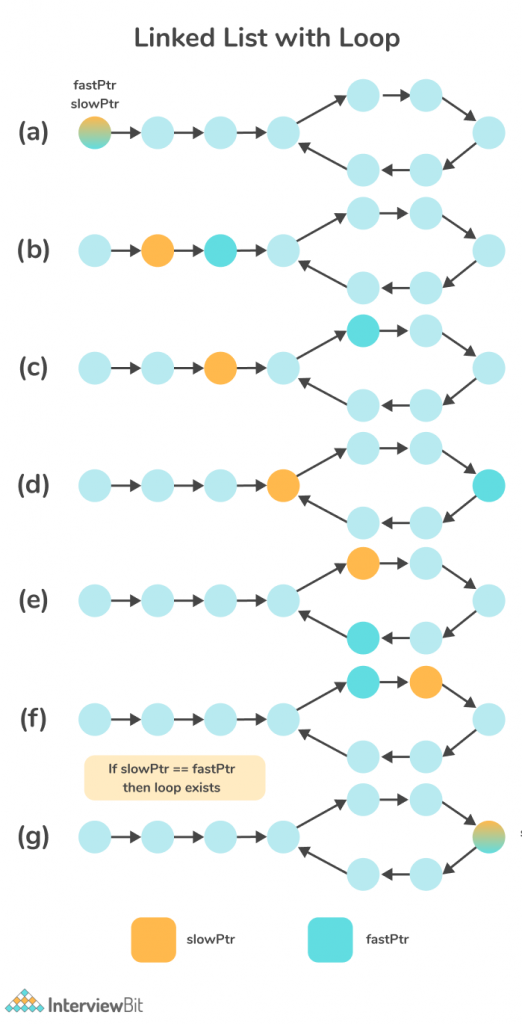
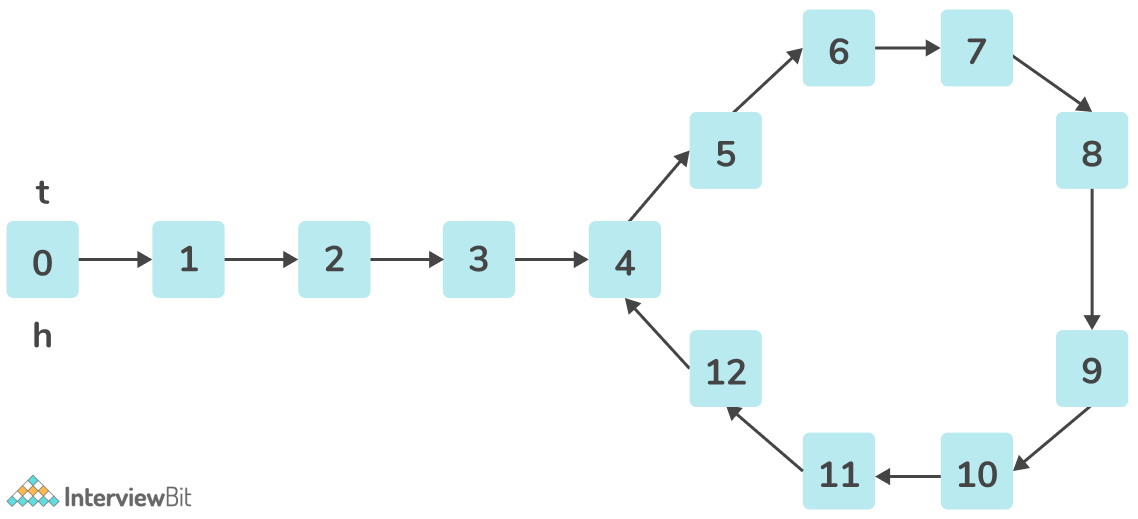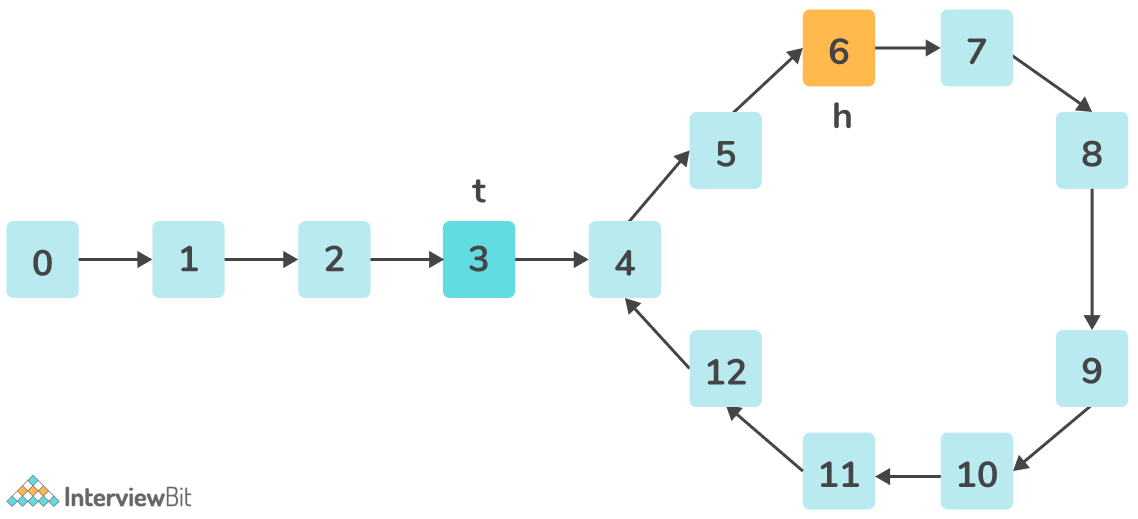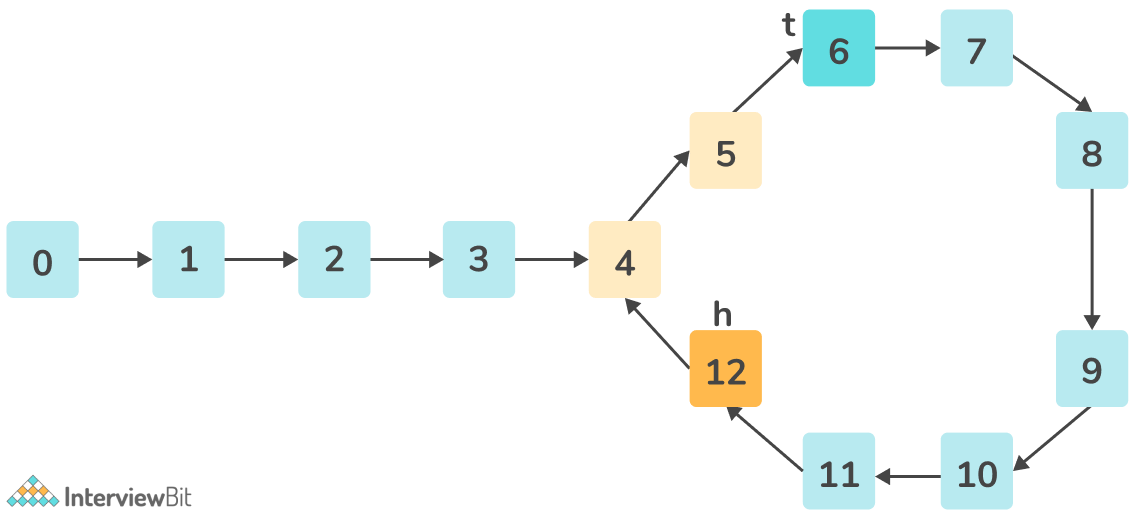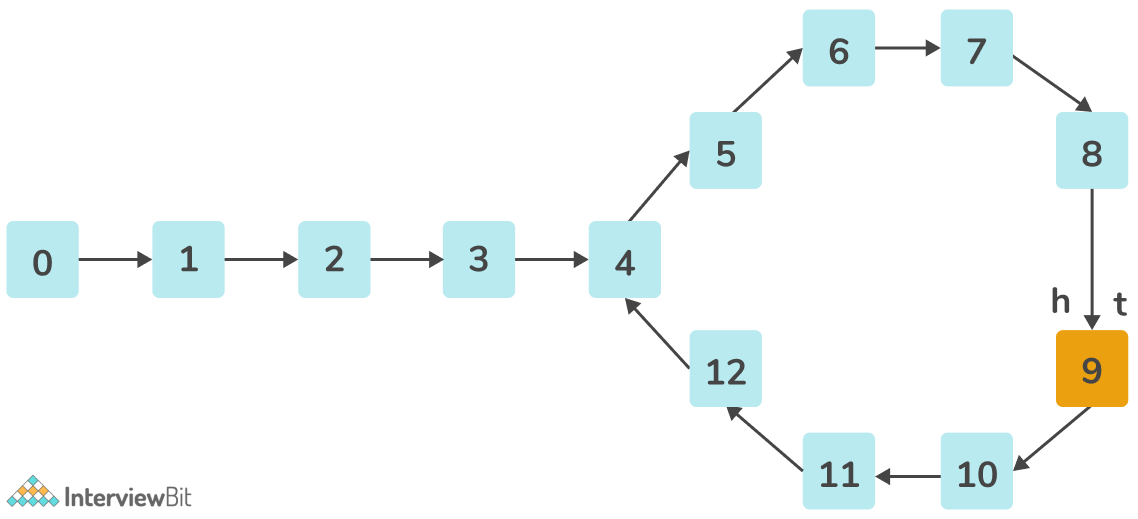
Algorithm

• Initialise two pointers, fast and slow to the head of the linked list.
• Traverse through the linked list until the fast pointer doesn’t reach the end of the linked list.
• If the fast pointer reaches the end, the linked list doesn’t contain any cycle. Hence, return False.
• Otherwise, move the slow pointer by one node i.e. slow = slow -> next and the fast pointer by two nodes i.e. fast = fast -> next -> next.
• At any point, if the fast and the slow pointers point to the same node, set node-> next = NULL and return True as a loop has been detected.

C++ Code

void removeCycle(Node * slow, Node * head) {
  for (Node * curr = head; curr != nullptr; curr = curr -> next) {
    Node * ptr = slow;
    while (ptr -> next != slow && ptr -> next != curr) {
      ptr = ptr -> next;
    }
    if (ptr -> next == curr) {
      ptr -> next = nullptr;
      return;
    }
  }
}
Node * identifyCycle(Node * head) {
  Node * slow = head, * fast = head;
 
  while (fast && fast -> next) {
    slow = slow -> next;
    fast = fast -> next -> next;
    if (slow == fast) {
      return slow;
    }
  }
  return nullptr;
}

Java Code

public static void removeCycle(Node slow, Node head) {
  for (Node curr = head; curr != null; curr = curr.next) {
    Node ptr = slow;
    while (ptr.next != slow && ptr.next != curr) {
      ptr = ptr.next;
    }
    if (ptr.next == curr) {
      ptr.next = null;
      return;
    }
  }
}
public static Node identifyCycle(Node head) {
  Node slow = head, fast = head;
 
  while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow == fast) {
      return slow;
    }
  }
  return null;
}

Python Code

def removeCycle(slow, head):
    curr = head
    while curr:
        ptr = slow
        while ptr.next is not slow and ptr.next is not curr:
            ptr = ptr.next
 
        if ptr.next == curr:
            ptr.next = None
            return
 
        curr = curr.next
 
 
def identifyCycle(head):
    slow = fast = head
 
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
        if slow == fast:
            return slow
 
    return None

• Time Complexity: O(N), where N is the number of nodes of the linked list.
• Space Complexity: O(1), as a map is used.

FAQs

Q.1: How do you detect a loop in a linked list?

Ans. A loop can be detected efficiently using the fast and slow pointer algorithm, where the fast pointer moves by two nodes and the slow pointer move by one node at a time. Read more here

Q.2: Will the fast and slow pointer always meet at some point if the list contains a cycle?

Ans. Yes, if the linked list contains a cycle, the fast and slow pointer will always meet at some point.