Trailing Zeroes in Factorial

Problem Statement

Given a number n, find the number of trailing zeroes in n!.

Sample Test Cases

Input 1: n = 5
Output 1: 1
Explanation 1: 5! = 120 which has only 1 trailing zero.

Input 2: n = 100
Output 2: 24
Explanation 2: The number of trailing zeroes of 100! can be found to have 24 trailing zeroes.

Naive Approach

The naive approach to solve this problem is to calculate the value of n! and then to find the number of trailing zeroes in it.

We can find the number of trailing zeroes in a number by repeatedly dividing it by 10 until its last digit becomes non-zero.

C++ Implementation

int getTrailingZeroes(int n) {
  int factorial = 1;
  for (int i = 1; i <= n; i++) {
    factorial *= i;
  }
  int zeroes = 0;
  while (factorial % 10 == 0) {
    zeroes++;
    factorial /= 10;
  }
  return zeroes;
}

Java Implementation

public static int getTrailingZeroes(int n) {
  int factorial = 1;
  for (int i = 1; i <= n; i++) {
    factorial *= i;
  }
  int zeroes = 0;
  while (factorial % 10 == 0) {
    zeroes++;
    factorial /= 10;
  }
  return zeroes;
}

Python Implementation

def getTrailingZeroes(n):
    factorial = 1
    zeroes = 0
    for i in range(1, n + 1):
        factorial *= i
    while factorial % 10 == 0:
        factorial //= 10
        zeroes += 1
    return zeroes

Complexity Analysis

• Time Complexity: O(n)
• Space Complexity: O(1)

Optimal Approach

Observe that number of trailing zeroes in a number will be the highest power of 10 present in the number. 

Now we know that 10ⁿ = 2ⁿ * 5ⁿ. So, the highest power of 10 will be equal to the minimum of the highest power of 2 and the highest power of 5 present in n!. We can observe that the highest power of 2 is always going to be less than or equal to the highest power of 5 in any value of n!. So, our problem boils down to finding the highest power of 5 in n!.

The highest power of a prime number p, present in any factorial is given by a formula known as Legendre’s Formula, 

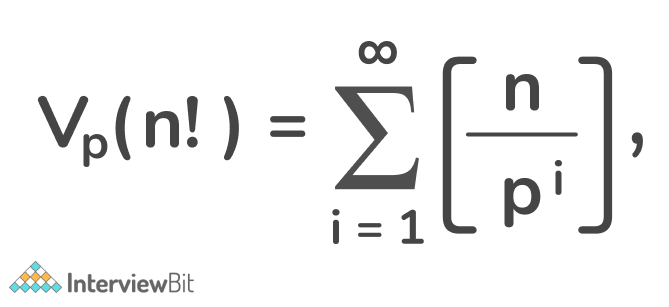
Where V_p(n!) represents the highest exponent in p, such that pⁿ divides n! where p is a prime number.

For the number of trailing zeroes, the above formula transforms to, 

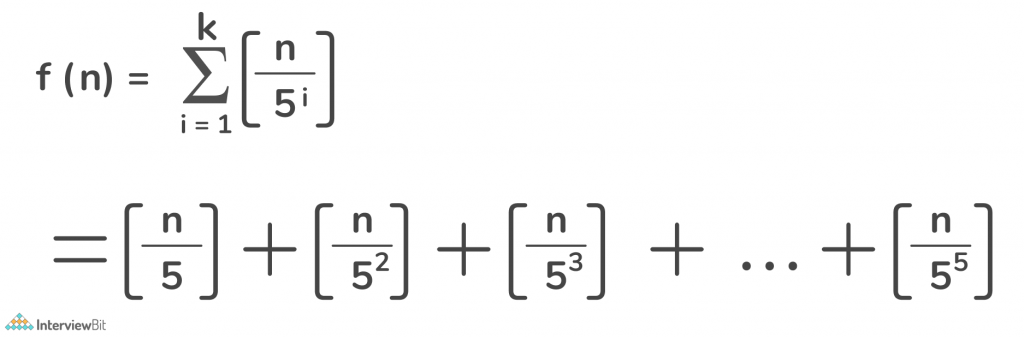
Where k = floor of log₅n.

C++ Code

int getTrailingZeroes(int n) {
  int zeroes = 0;
  int power = 5;
  for (int i = 1;; i++) {
    zeroes += (n / power);
    if (n / power == 0) {
      break;
    }
    power *= 5;
  }
  return zeroes;
}

Java Code

public static int getTrailingZeroes(int n) {
  int zeroes = 0;
  int power = 5;
  for (int i = 1;; i++) {
    zeroes += (n / power);
    if (n / power == 0) {
      break;
    }
    power *= 5;
  }
  return zeroes;
}

Python Code

def getTrailingZeroes(n):
    zeroes = 0
    power = 5
    while (n // power) != 0:
        zeroes += n // power
        power *= 5
    return zeroes

Complexity Analysis

• Time Complexity: O(log₅n)
• Space Complexity: O(1)

Practice Problem

Trailing Zeros

FAQs

Q. What is the main drawback of the naive approach?
A. The main drawback of the naive approach is that it calculates the factorial of n before computing the result, whose value can grow very large extremely quickly and can cause an overflow issue.

Q. How is the time complexity of the optimal approach calculated?
A. In the optimal approach, n is divided by 5 at each iteration till it reaches 0. So the number of iterations till which the algorithm will continue is equal to floor(log₅n), which is our required time complexity.