Count Inversions of an Array

Problem Statement

Given an array A of size N. The task is to count the total number of inversions of the array.

Inversions: A pair (A[i], A[j]) is said to be in inversion if:

• A[i] > A[j]
• i < j

Examples:

Input: A[] = [3, 2, 1]
Output: 3
Explanation:

The three pairs of inversions are – (3, 2) , (3, 1), (2, 1)

Input:  A[] = {6, 3, 5 ,2, 7}
Output: 5
Explanation:

The five pairs of inversions are – (6, 3) , (6, 5), (6, 2), (3, 2), (5, 2)

Approach 1: Brute Force

A simple approach is to consider every possible pair of the array and check if the pair satisfies the given condition. If true, increment count.

Algorithm:

• Initialise count = 0.
• Run a loop i from 0 to N and a nested loop j from i + 1 till N.
  • If A[i] > A[j], increment count
• Return count.

C++ Implementation

int getInversions(int * A, int n) {
  int count = 0;
  for (int i = 0; i < n; ++i) {
    for (int j = i + 1; j < n; ++j) {
      if (A[i] > a[j]) {
        ++count;
      }
    }
  }
  return count;
}

Java Implemenation

public static int getInversions(int[] A, int n) {
  int count = 0;
 
  for (int i = 0; i < n; i++) {
    for (int j = i + 1; j < n; j++) {
      if (A[i] > A[j]) {
        count += 1;
      }
 
    }
  }
  return count;
}

Python Implementation

def getInversions(A, n):
    count = 0
    for i in range(n):
        for j in range(i + 1, n):
            if A[i] > A[j]:
                count += 1
 
    return count

Time Complexity:O(N^2), where N is the total size of the array
Space Complexity:O(1), as no extra space has been used.

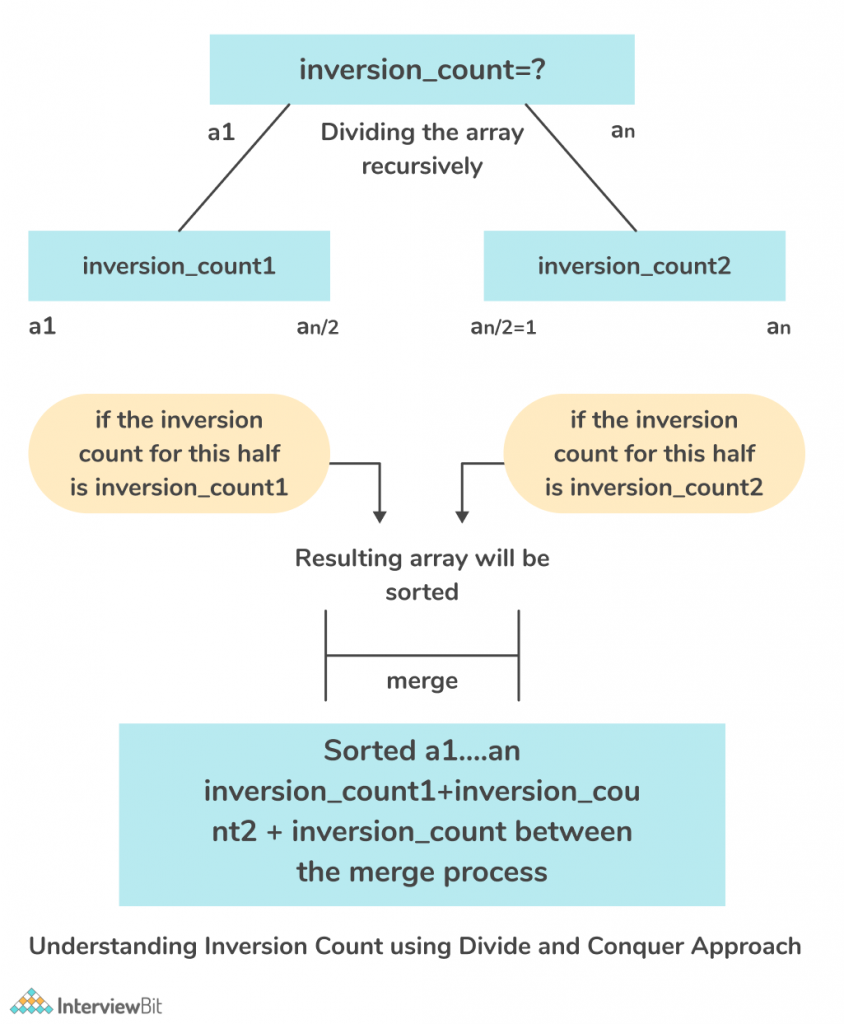
Approach 2: Merge Sort

The idea is to use a method similar to the merge sort algorithm. Like merge sort, divide the given array into two parts. For each left and right half, count the inversions, and at the end, sum up the inversions from both halves to get the resultant inversions.

Dry run of the above approach with an example:

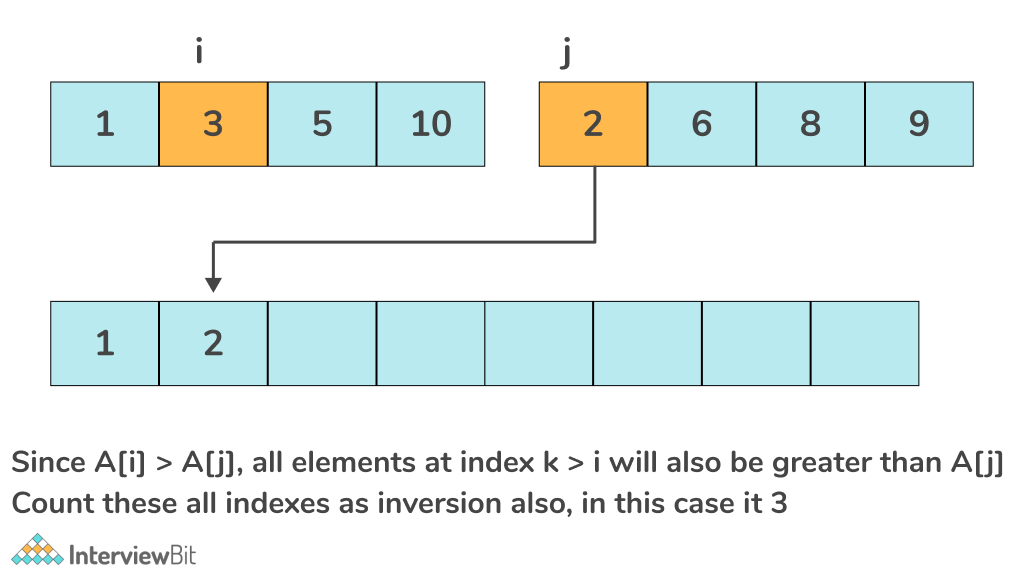
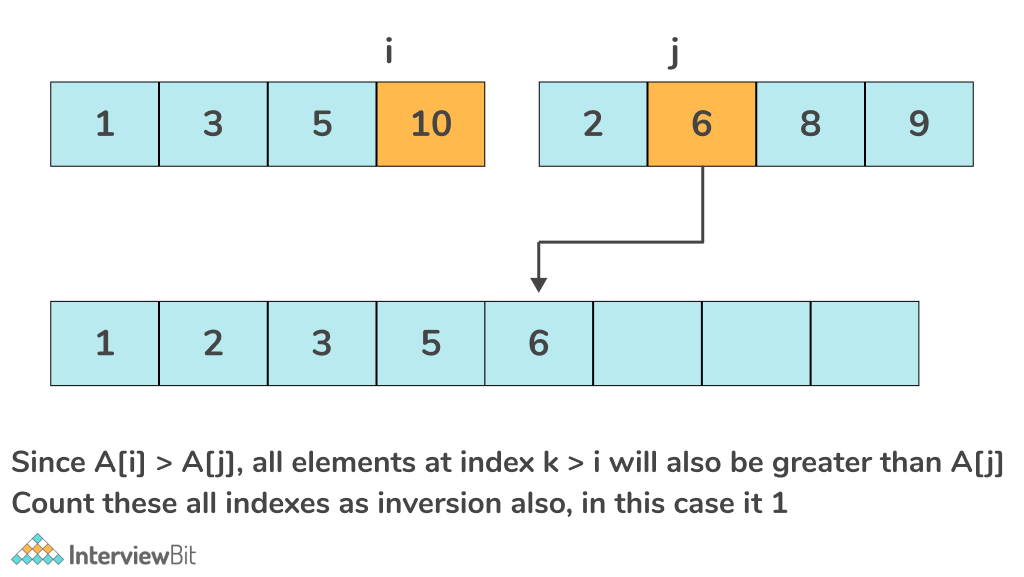
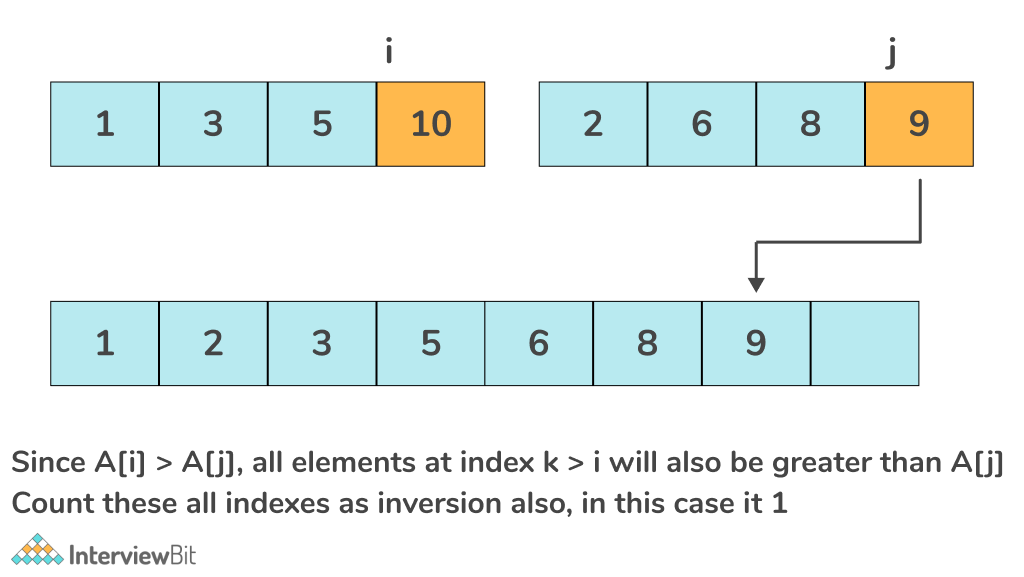
The total inversion count of the above array is 6.

The overall algorithm can be briefed as such :

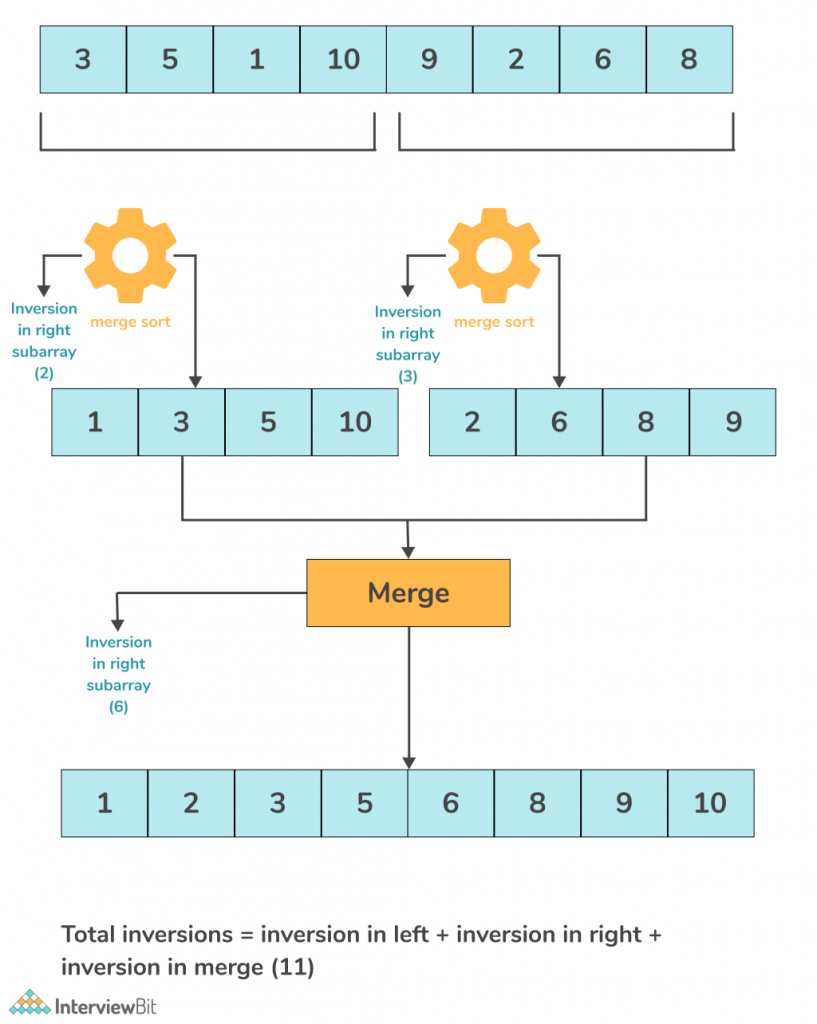
Algorithm

• Split the given input array into two halves, left and right similar to merge sort recursively.
• Count the number of inversions in the left half and right half along with the inversions found during the merging of the two halves.
• Stop the recursion, only when 1 element is left in both halves.
• To count the number of inversions, we will use a two pointers approach. Let us consider two pointers i and j, one pointing to the left half and the other pointing towards the right half.
• While iterating through both the halves, if the current element A[i] is less than A[j], add it to the sorted list, else increment the count by mid – i.

C++ Implementation

long long merge(long long arr[], int left, int mid, int right) {
  int i = left, j = mid, k = 0;
  long long invCount = 0;
  int temp[(right - left + 1)];
 
  while ((i < mid) && (j <= right)) {
    if (arr[i] <= arr[j]) {
      temp[k] = arr[i];
      ++k;
      ++i;
    } else {
      temp[k] = arr[j];
      invCount += (mid - i);
      ++k;
      ++j;
    }
  }
 
  while (i < mid) {
    temp[k] = arr[i];
    ++k;
    ++i;
  }
 
  while (j <= right) {
    temp[k] = arr[j];
    ++k;
    ++j;
  }
 
  for (i = left, k = 0; i <= right; i++, k++) {
    arr[i] = temp[k];
  }
 
  return invCount;
}
long long mergeSort(long long arr[], int left, int right) {
  long long invCount = 0;
 
  if (right > left) {
    int mid = (right + left) / 2;
    invCount = mergeSort(arr, left, mid);
    invCount += mergeSort(arr, mid + 1, right);
    invCount += merge(arr, left, mid + 1, right);
  }
  return invCount;
}
 
long long getInversions(long long arr[], int n) {
  return mergeSort(arr, 0, n - 1);
}

Java Implementation

private static long merge(long arr[], int left, int mid, int right) {
        int i = left, j = mid, k = 0;
        long invCount = 0;
        long temp[] = new long[(right - left + 1)];
 
        while ((i < mid) && (j <= right)) {
            if (arr[i] <= arr[j]) {
                temp[k] = arr[i];
                ++k;
                ++i;
            } 
            else {
                temp[k] = arr[j];
                invCount += (mid - i);
                ++k;
                ++j;
            }
        }
 
        while (i < mid) {
            temp[k] = arr[i];
            ++k;
            ++i;
        }
 
        while (j <= right) {
            temp[k] = arr[j];
            ++k;
            ++j;
        }
 
        for (i = left, k = 0; i <= right; i++, k++) {
            arr[i] = temp[k];
        }
 
        return invCount;
    }
    private static long mergeSort(long arr[], int left, int right) {
        long invCount = 0;
 
        if (right > left) {
            int mid = (right + left) / 2;
 
            invCount = mergeSort(arr, left, mid);
            invCount += mergeSort(arr, mid + 1, right);
            invCount += merge(arr, left, mid + 1, right);
        }
        return invCount;
    }
 
    public static long getInversions(long arr[], int n) {
        return mergeSort(arr, 0, n - 1);
    }

Python Implementation

def merge(arr, left, mid, right):
    i = left
    j = mid
    k = 0
    invCount = 0
    temp = [0 for x in range(right - left + 1)]
 
    while (i < mid) and (j <= right):
        if arr[i] <= arr[j]:
            temp[k] = arr[i]
            k += 1
            i += 1
 
        else:
            temp[k] = arr[j]
            invCount += mid - i
            k += 1
            j += 1
 
    while i < mid:
        temp[k] = arr[i]
        k += 1
        i += 1
 
    while j <= right:
        temp[k] = arr[j]
        k += 1
        j += 1
 
    k = 0
    for i in range(left, right + 1):
        arr[i] = temp[k]
        k += 1
 
    return invCount
 
 
def mergeSort(arr, left, right):
    invCount = 0
 
    if right > left:
        mid = (right + left) // 2
 
        invCount = mergeSort(arr, left, mid)
        invCount += mergeSort(arr, mid + 1, right)
        invCount += merge(arr, left, mid + 1, right)
 
    return invCount
 
 
def getInversions(arr, n):
    return mergeSort(arr, 0, n - 1)

Time Complexity:O(NlogN), where N is the total size of the array
Space Complexity:O(N), where N is the total size of the array

Practice Question

Inversions

FAQs

What does the count of inversions indicate in an array?
The count of inversion of an array indicates, how far the array is from being sorted in increasing order.

What is the most efficient approach to counting the number of inversions?
The merge sort approach is the most efficient approach to count the number of inversions. The time complexity is O(NlogN)