Longest Increasing Subsequence

Problem Statement

The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence of a given sequence such that all elements of the subsequence are sorted in increasing order.

For example, the length of LIS for {10, 22, 9, 33, 21, 50, 41, 60, 80} is 6 and LIS is {10, 22, 33, 50, 60, 80}.

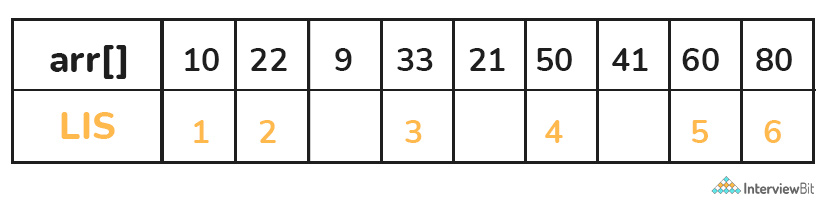
Example:

Input: arr[] = {5,4,1,2,3}
Output: Length of LIS = 3
Explanation: The longest increasing subsequence is 1,2,3

Input: arr[] = {7,5}
Output: Length of LIS = 1
Explanation: The longest increasing subsequences are {5} or {7}.

Simple Approach

• Let’s try to learn by taking an example.
• arr[] = {3,10,2,11}
• If we will think about any subsequence then it can start from anywhere so to figure this out we can apply a simple approach as to fix every index so that we can easily be able to calculate the subsequent at each ending index. And from this we can find recurrence relation.

lis_ending_here(arr, i) = 1 + lis_ending_here(arr, j) --> j < i and arr[j] < arr[i].

Recursive-tree of Simple Approach

Pseudo-Code

int lis_ending_here(int arr[], int curr) {
  // Only one subsequence ends at first index, the number itself
  if (curr == 0)
    return 1
  int ans = 1
  for (i = curr - 1 to 0, decrement of -1)
    if (arr[i] < arr[curr])
      ans = max(ans, 1 + lis_ending_here(arr, i))
  return ans
}
int longest_increasing_subsequence(int arr[], int N) {
  // Because a single number can be a subsequence too
  int max_ans = 1
  for (i = 0 to N - 1)
    max_ans = max(max_ans, lis_ending_here(arr, i))
  return max_ans
}

Time complexity: O(2^N), Where N is the size of the array.
Space complexity: O(N) for stack space in recursion.

Dynamic Programming Approach

If we will draw the recursion tree for the above approach then we can easily see in the below image, there are some overlapping subproblems and in which we can easily apply substructure properties. Hence we can say we can store some state and use it in dynamic programming.

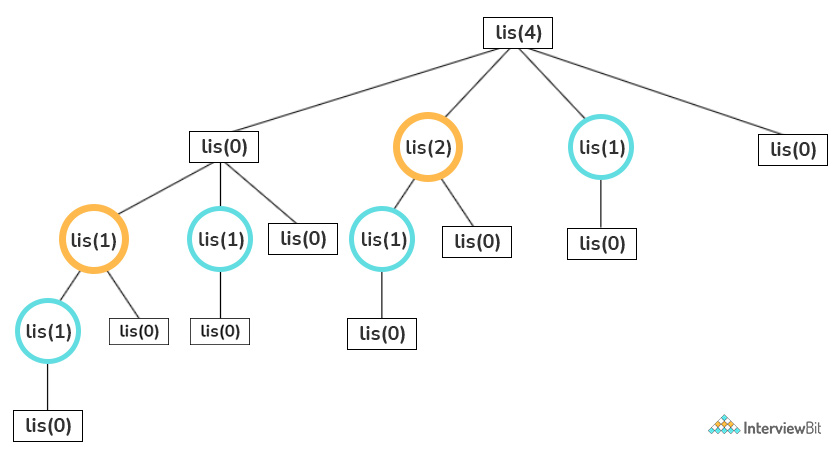
Elements of Dynamic Programming Approach

Here the recursion approach is top-down. Hence we can use it in the implementation of our dynamic programming bottom-up. What are the different states or elements that are possible for dynamic programmatic

We have to define problem variables: There is only one parameter on which the state of the problem depends i.e. which is N here, the size of the array.

We have to define size and table structure: For to write the code in a bottom-up manner we have to first define the size and table structure.

Dry Run of this approach

Input: arr[] = {3, 10, 2, 11}
LIS[] = {1, 1, 1, 1} (initially)

Iteration-wise simulation:

1. arr[2] > arr[1] {LIS[2] = max(LIS [2], LIS[1]+1 = 2}
2. arr[3] < arr[1] {No change}
3. arr[3] < arr[2] {No change}
4. arr[4] > arr[1] {LIS[4] = max(LIS [4], LIS[1]+1 = 2}
5. arr[4] > arr[2] {LIS[4] = max(LIS [4], LIS[2]+1 = 3}
6. arr[4] > arr[3] {LIS[4] = max(LIS [4], LIS[3]+1 = 3}

Implementation

C++ Implementation

Java Implementation

Python Implementation

Time complexity: O(N^2), Where N is the size of the array.
Space complexity: O(N)

Greedy With Binary Search: Efficient Approach

Let’s take an example and try to construct LIS from this example
Arr = [12, 16, 18, 13, 14, 15, 11]
First of all take the subsequence starting with an empty one: lis = [].
Let’s pick the first element, lis = [12].
16 is greater than the previous number, lis = [12, 16]
18 is greater than previous number, lis = [12, 16, 18]
13 is less than the previous number, we can’t extend the subsequence lis, but we must keep 13 because in the future there may be the longest subsequence starting with [12, 13], sub1 = [12, 16, 18], ans = [12, 13].
With 14, we can’t extend sub1, but we can extend sub2, so lis = [12, 16, 18], ans = [12, 13, 14].
With 15, we can’t extend sub1, but we can extend sub2, so lis = [12, 16, 18], ans = [12, 13, 14, 15].
With 11, we can’t extend neighter sub1 nor sub2, but we need to keep 1, so lis = [12, 16, 18], ans = [12, 13, 14, 15], new_lis = [11].

Finally, length of longest increase subsequence = len(sub2) = 4.

If we take a small example or Arr=[2,6,8,3,4,5,1] then the below picture shows how we are just maintaining our longest subsequence array.

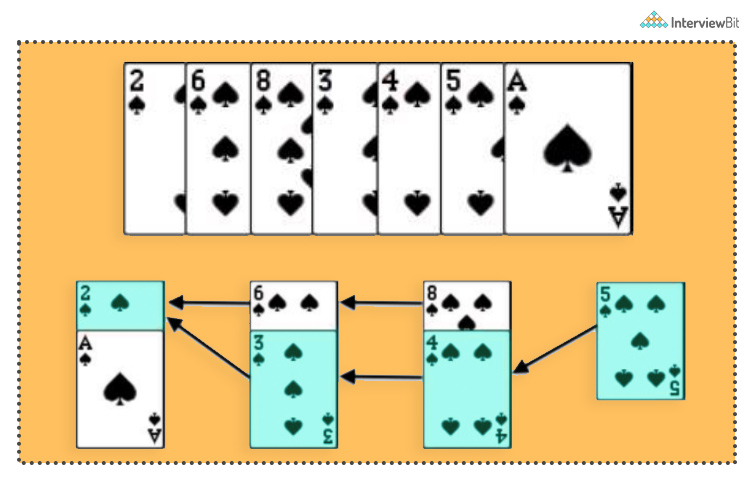
C++ Implementation of Greedy Approach

Java Implementation of Greedy Approach

Python Implementation of Greedy Approach

[BONUS CODE] Get Longest Increasing Subsequence Path

C++ Code

Python Code

Time Complexity: O(NlogN)
Space Complexity: O(N)

Practice Questions

• Length Of Longest Subsequence
• Longest Increasing Subsequence

Frequently Asked Questions

Q: What is an application of the longest common subsequence?
A: The longest common subsequence problem is a classic computer science problem, the basis of data comparison programs such as the difficulty, and has applications in computational linguistics and bioinformatics.

Q: Is the longest Increasing Subsequence NP hard?
A: No, as we can solve LIS in o(Nlogn) time complexity.