Maximum Subarray Sum: Kadane’s Algorithm

Problem Statement

Subarrays are arrays inside another array which only contains contiguous elements.

Given an array of integers, the task is to find the maximum subarray sum possible of all the non-empty subarrays.

Example:

Input: [-3, -4, 5, -1, 2, -4, 6, -1]
Output: 8
Explanation: Subarray [5, -1, 2, -4, 6] is the max sum contiguous subarray with sum 8.

Input: [-2, 3, -1, 2]
Output: 4
Explanation: Subarray [3, -1, 2] is the max sum contiguous subarray with sum 4.

We would be solving the problem by following approaches –

• Simple approach
• Efficient Approach: Kadane’s Algorithm

Simple Approach:

The simple approach to solve this problem is to run two for loops and for every subarray check if it is the maximum sum possible. Follow the below steps to solve the problem.

• Run a loop for i from 0 to n – 1, where n is the size of the array.
• Now, we will run a nested loop for j from i to n – 1 and add the value of the element at index j to a variable currentMax.
• Lastly, for every subarray, we will check if the currentMax is the maximum sum of all contiguous subarrays.

C implementation

C++ implementation

Java implementation

Python implementation

Time complexity: O(N^2), Where N is the size of the array.
Space complexity: O(1)

Efficient Approach: Kadane’s Algorithm

Kadane’s Algorithm is an iterative dynamic programming algorithm. It calculates the maximum sum subarray ending at a particular position by using the maximum sum subarray ending at the previous position. Follow the below steps to solve the problem.

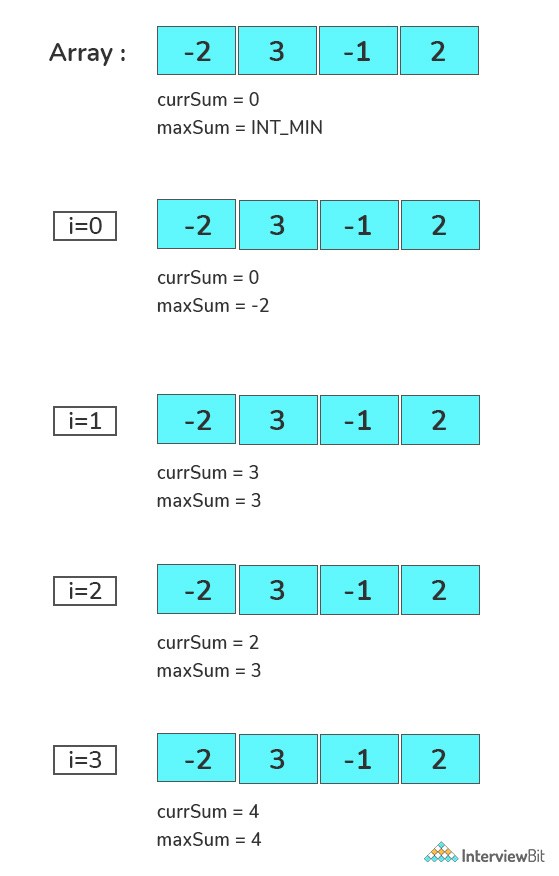
• Define two-variable currSum which stores maximum sum ending here and maxSum which stores maximum sum so far.
• Initialize currSum with 0 and maxSum with INT_MIN.
• Now, iterate over the array and add the value of the current element to currSum and check
  • If currSum is greater than maxSum, update maxSum equals to currSum.
  • If currSum is less than zero, make currSum equal to zero.
• Finally, print the value of maxSum.

Dry run of the above approach

C implementation of Efficient approach

C++ implementation of Efficient approach

Java implementation of Efficient approach

Python implementation of Efficient approach

Time complexity: O(N), Where N is the size of the array.
Space complexity: O(1)

Practice Problems –

Flip Problem
Maximum Product Subarray
Maximum Sum Contiguous Subarray

Frequently Asked Questions

Q. Is Kadane’s algorithm Dynamic Programming?
A. Yes, It is an iterative dynamic programming algorithm.

Q. What should be the maximum subarray sum if all the elements of the array are negative?
A. It depends if we are considering empty subarray or not. If we consider an empty subarray then the output should be 0 else, the output should be the maximum element of the array(the element closest to 0).

Q. What is the time complexity of Kadane’s algorithm?
A. The time complexity of Kadane’s algorithm is O(N) where N is the size of the array.