Table Of Contents
show
Problem Statement
Given a matrix of size M x N, where ‘1’ represents land, while ‘0’ represents water. The task is to return the number of islands present in the matrix. An island is a group of 1’s surrounded either vertically or horizontally.
Examples:
Input:
Confused about your next job?
In 4 simple steps you can find your personalised career roadmap in Software development for FREE
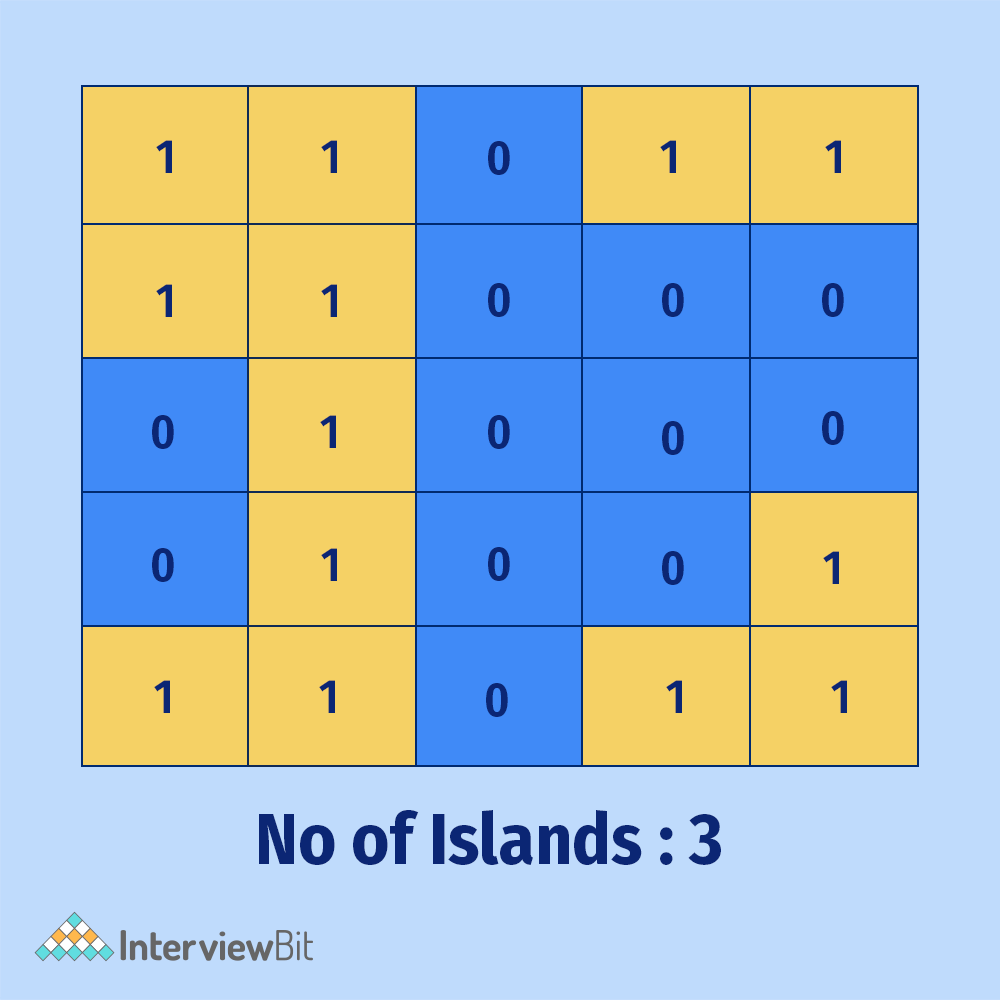
Output: 3
Explanation: Shown in the image
Approach 1: DFS
The idea is to consider the given matrix as a graph, where each cell is a node of the given graph. Two nodes contain an edge if and only if there is a ‘1’ either horizontally or vertically.
Algorithm
- Scan the matrix from (0,0) to (N, M).
- If the current element is ‘1’, start a DFS.
- In the DFS traversal, mark every visited node.
- Count the number of islands as the number of nodes that trigger the DFS.
- Return count.
C++ Code Implementation
void dfs(vector < vector < char >> & grid, int r, int c) {
int nr = grid.size();
int nc = grid[0].size();
grid[r][c] = '0';
if (r - 1 >= 0 && grid[r - 1][c] == '1') dfs(grid, r - 1, c);
if (r + 1 < nr && grid[r + 1][c] == '1') dfs(grid, r + 1, c);
if (c - 1 >= 0 && grid[r][c - 1] == '1') dfs(grid, r, c - 1);
if (c + 1 < nc && grid[r][c + 1] == '1') dfs(grid, r, c + 1);
}
int numIslands(vector < vector < char >> & grid) {
int nr = grid.size();
if (!nr) return 0;
int nc = grid[0].size();
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
dfs(grid, r, c);
}
}
}
return num_islands;
}Java Code Implementation
void dfs(char[][] grid, int r, int c) {
int nr = grid.length;
int nc = grid[0].length;
if (r < 0 || c < 0 || r >= nr || c >= nc || grid[r][c] == '0') {
return;
}
grid[r][c] = '0';
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int nr = grid.length;
int nc = grid[0].length;
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
dfs(grid, r, c);
}
}
}
return num_islands;
}Python Code Implementation
def numIslands(self, grid):
if not grid:
return 0
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == "1":
self.dfs(grid, i, j)
count += 1
return count
def dfs(self, grid, i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] != "1":
return
grid[i][j] = "#"
self.dfs(grid, i + 1, j)
self.dfs(grid, i - 1, j)
self.dfs(grid, i, j + 1)
self.dfs(grid, i, j - 1)- Time Complexity: O(M * N), where M and N are the size of the matrix
- Space Complexity: O(M * N).
Approach 2: BFS
The problem can also be solved using the BFS approach. The logic remains the same as the previous approach.
Algorithm
- Scan the matrix from (0,0) till (N, M).
- If the current element is ‘1’, start a BFS.
- Consider a queue and put the current node into the queue.
- Iteratively visit its neighbours vertically and horizontally and mark them as visited.
- The count is the total number of times the BFS has been invoked.
- Return count.
C++ Code Implementation
int numIslands(vector < vector < char >> & grid) {
int nr = grid.size();
if (!nr) return 0;
int nc = grid[0].size();
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
grid[r][c] = '0'; // mark as visited
queue < pair < int, int >> neighbors;
neighbors.push({
r,
c
});
while (!neighbors.empty()) {
auto rc = neighbors.front();
neighbors.pop();
int row = rc.first, col = rc.second;
if (row - 1 >= 0 && grid
== '1') {
neighbors.push({
row - 1,
col
});
grid
= '0';
}
if (row + 1 < nr && grid
== '1') {
neighbors.push({
row + 1,
col
});
grid
= '0';
}
if (col - 1 >= 0 && grid
== '1') {
neighbors.push({
row,
col - 1
});
grid
= '0';
}
if (col + 1 < nc && grid
== '1') {
neighbors.push({
row,
col + 1
});
grid
= '0';
}
}
}
}
}
return num_islands;Java Code Implementation
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int nr = grid.length;
int nc = grid[0].length;
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
grid[r][c] = '0'; // mark as visited
Queue < Integer > neighbors = new LinkedList < > ();
neighbors.add(r * nc + c);
while (!neighbors.isEmpty()) {
int id = neighbors.remove();
int row = id / nc;
int col = id % nc;
if (row - 1 >= 0 && grid
== '1') {
neighbors.add((row - 1) * nc + col);
grid
= '0';
}
if (row + 1 < nr && grid
== '1') {
neighbors.add((row + 1) * nc + col);
grid
= '0';
}
if (col - 1 >= 0 && grid
== '1') {
neighbors.add(row * nc + col - 1);
grid
= '0';
}
if (col + 1 < nc && grid
== '1') {
neighbors.add(row * nc + col + 1);
grid
= '0';
}
}
}
}
}
return num_islands;
}Python Code Implementation
from collections import deque
def numIslands(grid):
if not grid:
return 0
lands = set(
[
(i, j)
for j in xrange(len(grid[0]))
for i in xrange(len(grid))
if grid[i][j] == "1"
]
)
count = 0
while lands:
count += 1
i, j = lands.pop()
connected = deque()
connected.append((i, j))
while connected:
i, j = connected.popleft()
if (i + 1, j) in lands:
connected.append((i + 1, j))
lands.remove((i + 1, j))
if (i - 1, j) in lands:
connected.append((i - 1, j))
lands.remove((i - 1, j))
if (i, j + 1) in lands:
connected.append((i, j + 1))
lands.remove((i, j + 1))
if (i, j - 1) in lands:
connected.append((i, j - 1))
lands.remove((i, j - 1))
return countTime Complexity:O(M * N), where M and N is the size of the matrix
Space Complexity:O(min(M,N)).
Practice Question
FAQs
Q.1: What is the time and space complexity of the DFS approach?
Ans: The time and space complexity of the DFS approach is O(M * N) and O(M * N).
Q.2: In terms of space complexity, is the BFS approach efficient over DFS?
Ans: Yes, the space complexity for the BFS approach is O(min(N,M)), in the worst case when the grid is filled completely with 1’s, whereas for DFS it is O(N*M).
