Given a binary tree of integers. The task is to return an array of integers representing the bottom view of the Binary tree.
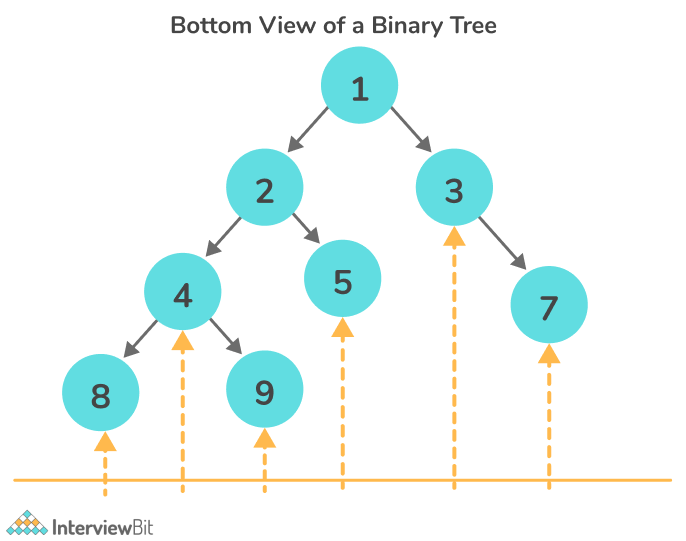
Bottom view of a Binary Tree: is a set of nodes visible when the tree is visited from the bottom.
Examples:
Input:
Confused about your next job?
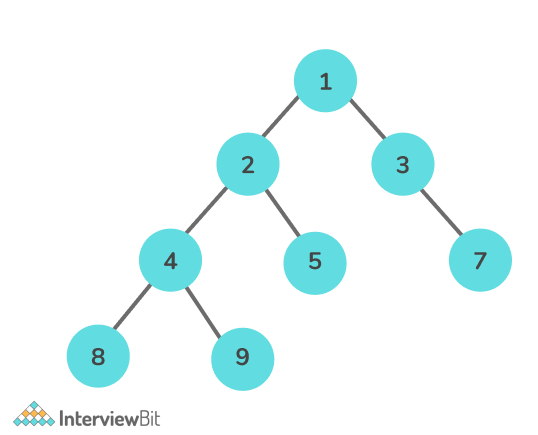
Output: [8, 4, 9, 5, 3, 7]
Explanation:
Input:
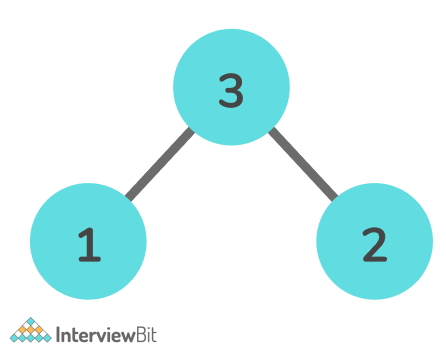
Output: [1, 3, 2]
Hashmap and Recursion Approach
The bottom view of a binary tree refers to the bottommost nodes present at the same level.
Algorithm
- Perform a preorder traversal to calculate the level of each node of the binary tree.
- Consider a hashmap and store the height into the map, where the key is the level or the horizontal distance of the ith node and the value is a pair (p, q), where p is the value of the node and q is the height of the node.
- For every node:
- Add the node to the resultant map if it is the first node to have the current horizontal distance.
- Else, if a node is already present for the particular distance, replace the previous node with the current node, if the node has a height greater than the previous node.
C++ Code
void bottomview(Tree * root, map<int,vector<int>>& m, int lev, int h_dist){
if (root == NULL)
return;
if (m.find(h_dist) == m.end()) {
m[h_dist].push_back(lev);
m[h_dist].push_back(root -> data);
}
else {
if (m[h_dist][0] <= lev) {
m[h_dist][0] = lev;
m[h_dist][1]= root -> data;
}
}
// Calling the function for the right and left subtrees
// with the appropriate parameters.
bottomview(root -> left, m, lev + 1, h_dist - 1);
bottomview(root -> right, m, lev + 1, h_dist + 1);
}
Void print_bottom_of_binary_tree(Tree* root){
map<int,vector<int>> Map;
bottomview(root, Map, 1, 0);
for (auto it = Map.begin(); it != Map.end(); ++it)
{
cout << (it-> second)[1]<< " ";
}
}Java Code
bottomview(Node root, TreeMap<Integer, int[]> m, int curr, int hd)
{
if (root == null)
return;
if (!m.containsKey(hd))
{
m.put(hd, new int[]{ root.data, curr });
}
else
{
int[] p = m.get(hd);
if (p[1] <= curr)
{
p[1] = curr;
p[0] = root.data;
}
m.put(hd, p);
}
printBottomViewUtil(root.left, curr + 1, hd - 1, m);
printBottomViewUtil(root.right, curr + 1,hd + 1, m);
}
print_bottom_of_binary_tree(Node root)
{
TreeMap<Integer, int[]> m = new TreeMap<>();
printBottomViewUtil(root, 0, 0, m);
for(int val[] : m.values())
{
System.out.print(val[0] + " ");
}
}Python Code
def print_bottom_of_binary_tree(root):
d = dict()
printBottomViewUtil(root, d, 0, 0)
for i in sorted(d.keys()):
print(d[i][0], end = " ")
def bottomview(root, d, hd, level):
if root is None:
return
if hd in d:
if level >= d[hd][1]:
d[hd] = [root.data, level]
else:
d[hd] = [root.data, level]
bottomview(root.left, d, hd - 1,level + 1)
bottomview(root.right, d, hd + 1,level + 1)Time Complexity: O(N) where N is the number of nodes of the binary tree.
Space Complexity: O(N), as a map is used.
Queue Approach
The approach is to perform a level order traversal of the given binary tree and store them in a queue. Also, consider a map, which stores the horizontal distance of the nodes from root as the key.
Algorithm
- Initialise a queue to store the nodes on performing level order traversal.
- Push the root of the binary tree into the queue along with its horizontal distance(hd), which is 0.
- Keep on pushing the left child to the queue along with their horizontal distance as hd – 1 and right child as hd + 1.
- While the queue is not empty, perform the following operations:
- Store the front element of the queue is a variable, say, res.
- Pop the element.
- Put the dequeued element, stored in res and update its value in the map.
- If a left child is present, push the left child into the queue along with its horizontal distance as hd – 1.
- If a right child is present, push the right child into the queue along with its horizontal distance as hd + 1.
- Print the values in the map which contains the bottom key of the binary tree.
C++ Implementation of Queue Method
void bottomview(Tree * root){
int horizontalDistance = 0;
map<int, Tree*> mp;
queue<pair<Tree*, int>> q;
q.push({root, 0});
while (!q.empty()) {
pair<BinaryTreeNode<int> *, int> p = q.front();
q.pop();
mp[p.second] = p.first;
if (p.first->left != NULL) {
q.push({p.first->left, p.second - 1});
}
if (p.first->right != NULL) {
q.push({p.first->right, p.second + 1});
}
}
for (auto i = mp.begin(); i != mp.end(); i++) {
cout <<(i->second->data) <<” “;
}
}Java Implementation of Queue Method
class Pair {
Tree root;
int level;
Pair() {
}
Pair(Tree root, int level) {
this.root = root;
this.level = level;
}
}
bottomView(BinaryTreeNode root) {
int horizontalDistance = 0;
ArrayList<Integer> ans = new ArrayList<>();
HashMap<Integer, BinaryTreeNode> mp = new HashMap<>();
Queue<Pair> q = new LinkedList<>();
Pair p1 = new Pair(root, 0);
q.add(p1);
while (!q.isEmpty()) {
Pair p = q.poll();
mp.put(p.level, p.root);
if (p.root.left != null) {
q.add(new Pair(p.root.left, p.level - 1));
}
if (p.root.right != null) {
q.add(new Pair(p.root.right, p.level + 1));
}
}
ArrayList<Integer> bottomView = new ArrayList<>();
for (int key : mp.keySet()) {
bottomView.add(key);
}
Collections.sort(bottomView);
for (int i : bottomView) {
System.out.print(mp.get(i).val + “ “);
}
}
}Python Implementation of Queue Method
class Pair:
def __init__(self, root, level):
self.root = root
self.level = level
def bottomView(root):
horizontalDistance = 0
mp = OrderedDict()
q = []
p1 = Pair(root, 0)
q.append(p1)
while len(q) > 0:
p = q.pop(0)
mp[p.level] = p.root
if p.root.left is not None:
q.append(Pair(p.root.left, p.level - 1))
if p.root.right is not None:
q.append(Pair(p.root.right, p.level + 1))
bottomViewList = []
for key in mp.keys():
bottomViewList.append(key)
bottomViewList.sort()
for i in bottomViewList:
print(mp.get(i).data, end = “ ”)Time Complexity: O(N * log N) where N is the number of nodes of the binary tree.
Space Complexity: O(N), as a map is used.
Practice Questions
Vertical Order traversal of Binary Tree
Right view of Binary tree
Frequently Asked Questions
What is the left view of a binary tree?
The set of nodes visible when the tree is visited from the left is the left view of the binary tree.
How do you print the bottom of a binary tree?
The bottom view of a binary tree can be printed by hashing and level order traversal of the binary tree.
What is the diameter of a binary tree?
The diameter of a tree is the number of nodes on the longest path between two leaves in the tree




