What is Print Left View of a Binary Tree Problem?
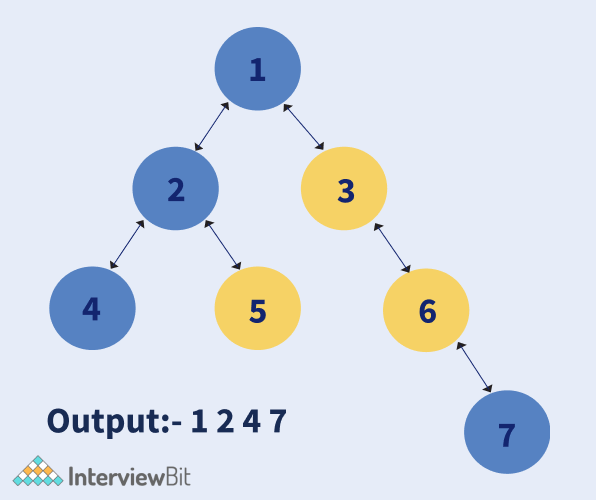
Given a binary tree, the left view of a binary tree is the set of all those nodes visible from the left side of the binary tree. In other words it is the set of first node of every level.
Method-1 (Using Recursion)
The left view contains all nodes that are first in every level. A simple solution is to do level order traversal (traversing the tree level by level) and print the first node in every level.
Confused about your next job?
This problem can be solved with the help of using simple recursion. Basically the idea is to print all the first nodes in every level. For this, we just keep visiting the left subtree before the right subtree with the height as a parameter of their respective nodes. The idea is to keep track of the maximum level that is already visited, if the current level is greater then the maximum level then print that node because that node is the first in its level.
Below is the implementation of the above idea-
C++ Code
// C++ program to print left view of Binary Tree
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int val;
struct Node *left, *right;
};
// A function to
// create a new Binary Tree Node
struct Node *newNode(int data)
{
struct Node *temp = new Node();
temp->val = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
// A Recursive function to print the nodes
// of left view of a binary tree.
void leftView(struct Node *root, int level, int *max_level)
{
// Base Case
if (root == NULL) return;
// If this is the left most Node of its level
if (*max_level < level)
{
cout << root->val << " ";
*max_level = level;
}
// Recur call for left subtree first,
// then right subtree
leftView(root->left, level + 1, max_level);
leftView(root->right, level + 1, max_level);
}
// Driver Code
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->right = newNode(6);
root->right->right->right = newNode(7);
int max_level = 0;
leftView(root, 1, &max_level);
return 0;
}Java Code
// A Recursive function to print the nodes
// of left view of a binary tree.
void leftViewUtil(Node node, int level)
{
// Base Case
if (node == null)
return;
// If this is the left most Node of its level
if (max_level < level) {
System.out.print(" " + node.val);
max_level = level;
}
// Recur call for left subtree first,
// then right subtree
leftViewUtil(node.left, level + 1);
leftViewUtil(node.right, level + 1);
}Python Code
def leftView(root, level, max_level):
# Base Case
if root is None:
return
# If this is the first node of its level
if (max_level[0] < level):
print "% d\t" %(root.val),
max_level[0] = level
# Recur for left and right subtree
leftViewUtil(root.left, level + 1, max_level)
leftViewUtil(root.right, level + 1, max_level)Time Complexity: Just a dfs traversal of a binary tree, Time Complexity of the above approach is O(n).
Auxiliary Space: O(n), due to the stack space during recursive call.
Method-2 (Using Queue):
In this method,a solution based on level order traversal is discussed. Our main aim to solve this problem is to find the left most node of every level. So we will solve this by using a simple level order traversal and print the leftmost node at every level. For this, we’ll use queue to store all the nodes in the current level,
- we’ll print out the first node and,
- loop through the nodes in the queue and,
- push all the child nodes and pop the parent out, basically this will give us the nodes present in the next level and,
- repeat the steps until the queue is empty.
Code for above implementation,
C++ Code
// function to print left view of
// binary tree
void LeftView(Node* root)
{
if (root==NULL)
return;
queue<Node*> q;
q.push(root);
while (!q.empty())
{
// number of nodes at current level
int n = q.size();
// function to print left view of
// binary tree
cout<<q.front()->data<<" ";
// Traverse all nodes of current level
for(int i = 0; i < n; i++)
{
Node* temp = q.front();
q.pop();
// Add left node to queue
if (temp->left != NULL)
q.push(temp->left);
// Add right node to queue
if (temp->right != NULL)
q.push(temp->right);
}
}
}Java Code
private static void LeftView(Node root)
{
if (root == null)
return;
Queue<Node> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
// number of nodes at current level
int n = q.size();
// Print the left most element at
// the level
System.out.print(q.poll().data + " ");
// Traverse all nodes of current level
for (int i = 0; i < n; i++) {
Node temp = q.poll();
// Add left node to queue
if (temp.left != null)
q.add(temp.left);
// Add right node to queue
if (temp.right != null)
q.add(temp.right);
}
}
}Python Code
def printRightView(root):
if (not root):
return
q = []
q.append(root)
while (len(q)):
# number of nodes at current level
n = len(q)
# Print the left most element
# at the level
print(q[0].data, end=" ")
# Traverse all nodes of current level
for i in range(0, n):
temp = q[0]
q.pop(0)
# Add left node to queue
if (temp.left != None):
q.append(temp.left)
# Add right node to queue
if (temp.right != None):
q.append(temp.right)Time Complexity: O(n), where n is the number of nodes in the binary tree.
Practice Problem
FAQs
- What is level order traversal ?
Level order traversal is travelling tree level by level.
- Can we find the left view of a binary tree using preorder traversal?
Yes, we just have to keep a track of current height for a node and if we visit a height for the first time we’ll print that element out.
- How to print the right view of a binary tree?
Right view is basically the right most element in a level thus we can use the same approach as mentioned above but instead of the first node we’ll print the last node.




