Top view of Binary Tree

Problem Statement

Binary Tree – A structure in which nodes are connected with each other in such a manner that every node can have a maximum of two children.

Top view – set of nodes that are visible when viewing from the top. To print the top view of the binary tree we can print those nodes in any order 

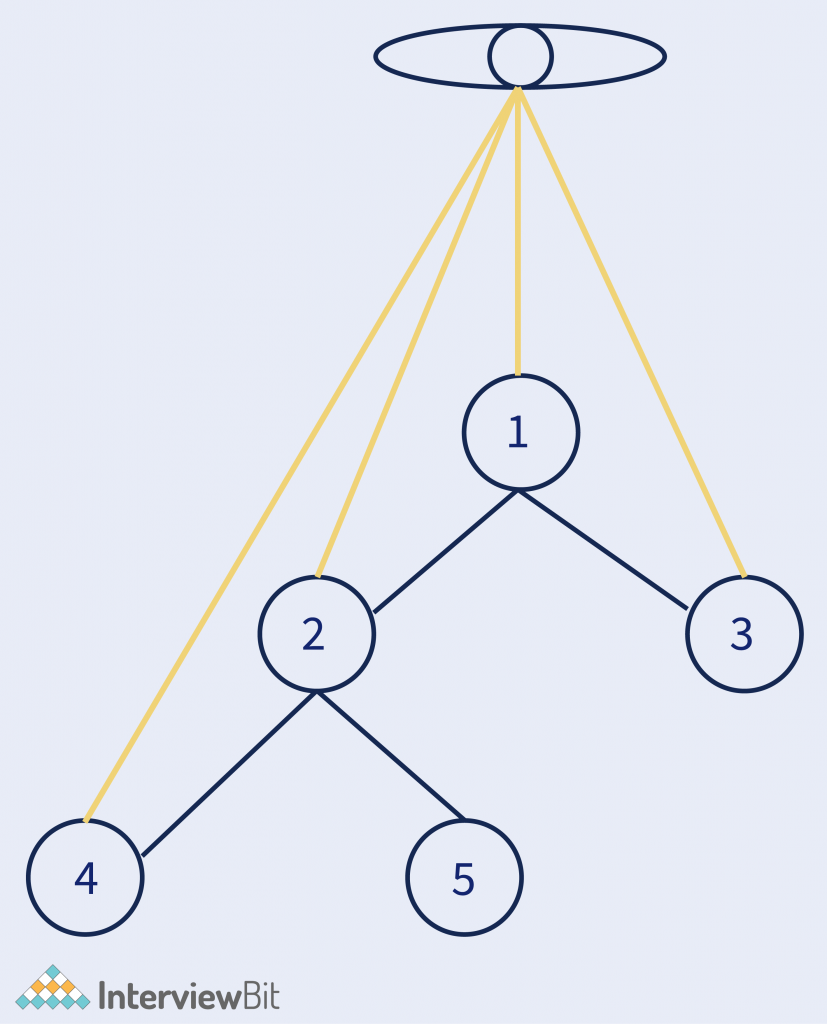
Output of the above tree – 4 2 1 3 

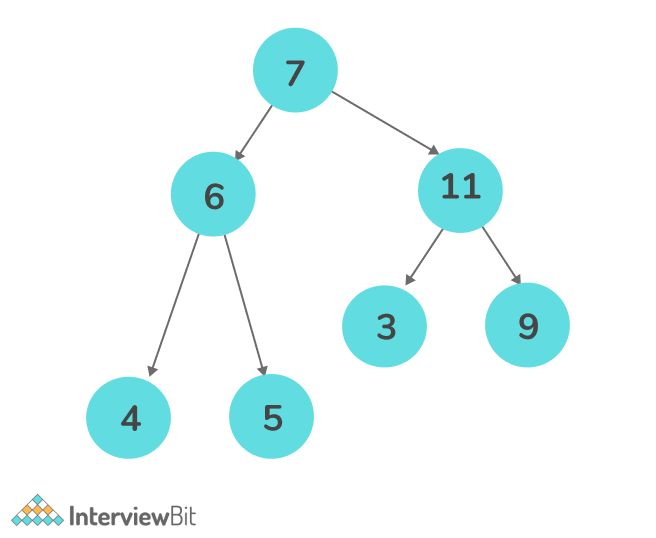
Example –

Output: 4 6 7 11 9
Explanation: As the nodes, 7,3,5 overlaps so we took only the top element as it’s the only node that can be viewed from the top.

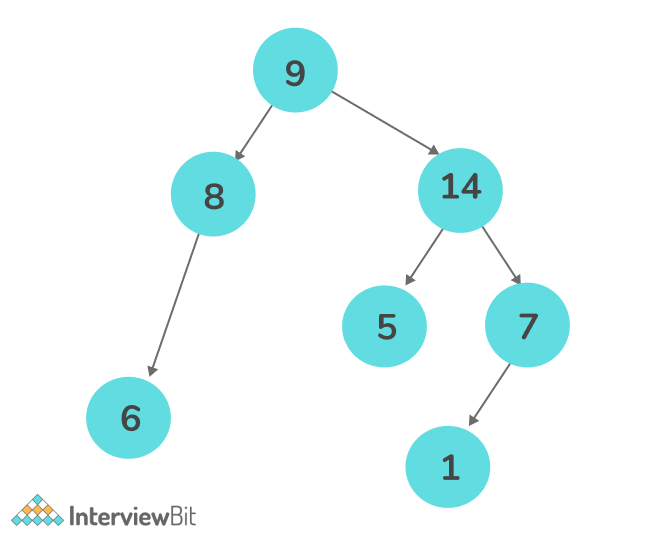
Example –

Output: 8 9 14 7
Explanation: As the nodes 9,5,6 and 14,1 overlap so we took only the top elements from each overlapping set as it’s the only node that can be viewed from the top.

Approach

The approach is to use the preorder traversal of the tree to traverse the tree and check that we have visited the current vertical level and if visited then we can check for the smaller horizontal level node and store it. Else we can just update the vertical level as visited and store the node and horizontal level of the current node.

• We have to create the map to check whether the horizontal level is visited or not as it will state the horizontal distance of the node from the root node. Where key will represent the horizontal distance and the value is the pair containing the value and level of each node.
• We will traverse the tree using the preorder traversal.
• Every time we check if the level of the current horizontal distance is less than the max level seen till now then we will update the value and the level for this horizontal distance.
• We will pass level-1 for the left child and level+1 for the right child to get the vertical level.
• Print the values present in the map.

C++ Code

void Topview(Tree * head, int dis, int level, auto & mp) {
  if (head == nullptr) {
    return;
  }
  if (mp.find(dis) == mp.end() || level < mp[dis].second) {
    mp[dis] = {
      head -> key,
      level
    };
  }
  Topview(head -> left, dis - 1, level + 1, mp);
  Topview(head -> right, dis + 1, level + 1, mp);
}
void Topview(Tree * head) {
  mp < int, pair < int, int >> mp;
  Topview(head, 0, 0, mp);
  for (auto it: mp) {
    cout << it.second.first << " ";
  }
}

Java Code

class Pair < U, V > {
  public final U first;
  public final V second;
  private Pair(U first, V second) {
    this.first = first;
    this.second = second;
  }
  public static < U,
  V > Pair < U,
  V > of (U a, V b) {
    return new Pair < > (a, b);
  }
}

class Main {
  public static void topView(Tree head, int dis, int level,
    Map < Integer, Pair < Integer, Integer >> map) {
    if (head == null) {
      return;
    }
    if (!map.containsKey(dis) || level < map.get(dis).second) {
      map.put(dis, Pair.of(head.key, level));
    }
    topView(head.left, dis - 1, level + 1, map);
    topView(head.right, dis + 1, level + 1, map);
  }
  public static void topView(Tree head) {
    Map < Integer, Pair < Integer, Integer >> map = new TreeMap < > ();
    topView(head, 0, 0, map);
    for (Pair < Integer, Integer > it: map.values()) {
      System.out.print(it.first + " ");
    }
  }
}

Python Code

def topView(head, dis, level, dict):

    if head is None:
        return

    if dis not in dict or level < dict[dis][1]:
        dict[dis] = (head.key, level)
    topView(head.left, dis - 1, level + 1, dict)
    topView(head.right, dis + 1, level + 1, dict)

def printTopView(head):
    dict = {}

    topView(head, 0, 0, dict)
    for key in sorted(dict.keys()):
        print(dict.get(key)[0], end=' ')

Time complexity: O(N), Where N is the size of the array.
Space complexity: O(1)

Practice Question

Vertical Order Traversal

FAQs

How do you find the top view of a tree?
We have to find the nodes which are visible from the top so we can find it recursively storing
The horizontal distance of every node from the root node.

What is a treetop view?
It’s the set of nodes visible when a tree is viewed from the top.

Additional Resources

• Binary Tree
• Level Order Traversal of Binary Tree
• Diameter of a Binary Tree
• Bottom View of Binary Tree
• Inorder Traversal of a Binary Tree
• Left View of a Binary Tree