Before going into Hashing techniques, let us understand certain key terms that are used in hashing.

Hash Table

A hash table is an array that stores pointers to data mapping to a given hashed key.

• Hash table uses hash function to compute index of array where a record will be inserted or searched. Basically, there are 2 main components of hash table: Hash function and array.
• A value in hash table is null if no existing key has hash value equal to the index for the entry.
• The average time complexity needed to search for a record in hash table is O(1) under reasonable assumptions.
• The maximum size of the array is according to the amount of data expected to be hashed. 

• On the previous slide, we introduced the notion of hashing, mapping a piece of data such as a string to some kind of a representative integer value. We can then create a map by using this hash as an index into an array of key/value pairs. Such a structure is generally called a hash table or, Hashmap in Java, or dictionary in Python, or unordered_map in C++ ( Sorry C users, you will have to implement your own hashmap ). We saw that using the string length to create the hash, and indexing a simple array, could work in some restricted cases, but is no good generally: for example, we have the problem of collisions (several keys with the same length) and wasted space if a few keys are vastly larger than the majority.

  Buckets

  Now, we can solve the problem of collisions by having an array of (references to) linked lists rather than simply an array of keys/values. Each little list is generally called a bucket.

  Then, we can solve the problem of having an array that is too large simply by taking the hash code modulo a certain array size3. So for example, if the array were 32 positions in size (going from 0-31 ), rather than storing a key/value pair in the list at position 33, we store it at position (33 mod 32) = 1. (In simple terms, we “wrap round” when we reach the end of the array.) So we end up with a structure something like this:

  Each node in the linked lists stores a pairing of a key with a value. Now, to look for the mapping for, say, Ireland, we first compute this key’s hash code (in this case, the string length, 7). Then we start traversing the linked list at position 7 in the table. We traverse each node in the list, comparing the key stored in that node with Ireland. When we find a match, we return the value from the pair stored in that node (Dublin). In our example here, we find it on the second comparison. So although we have to do some comparisons, if the list at a given position in the table is fairly short, we’ll still reduce significantly the amount of work we need to do to find a given key / value mapping.

  The structure we have just illustrated is essentially the one used by Java’s hash maps and hash sets. However, we generally wouldn’t want to use the string length as the hash code.

• Let us see how we can convert an object into a hash code more effectively by using hash functions in the next section rather than just using string length as the hashing algorithm.

Hash Functions

A hash function is a function or algorithm that is used to generate the encrypted or shortened value to any given key. The resultant of hash function is termed as a hash value or simply hash.

Properties of good hash function:

• Should be a one-way algorithm. In simple words, the hash value generated should not be converted back into the original key. 
• Should be efficiently computable. In real applications, if our algorithm takes longer time to compute the hash value itself from a hash function, then we lose the purpose of hashing.
• Should uniformly distribute the keys among the available records. 

Types of Hash Functions:

• Index Mapping Method: The most trivial form of hashing technique is called “Index Mapping (or Trivial Hashing)”. Here:

  • We consider an array where in the value of each position of the array corresponds to a key in the given list of keys.
  • This technique is very effective when the number of keys are reasonably small. It ensures that allocating one position of the array for every possible key is affordable.
  • Here, the hash function just takes the input and returns out the same value as output. 
  • This is effective only because it considers that any retrieval takes only O(1) time.
  • But otherwise, this approach is very trivial and inefficient to be used in real life scenarios as it assumes that the values are integers whereas in real life, we might have any datatype of data. Also, even for the case of integers, if the data is large, this is not suitable.

• Division method:

  • Here, for hash functions, we map each key into the slots of hash table by taking the remainder of that key divided by total table size available i.e h(key) = key % table_length  => h(key) = key MODULO table_length 
  • This method is quite fast since it takes help of a single division operation and is most commonly used.
  • Things to keep in mind while using division method:
    • Certain values of table size is avoided for effective performance. For example: the size of table should not be a power, say p of certain number, say r such that if table_length = r^p, then h(key) accomodates p lowest-order bits of key. We need to ensure that hash function we design depends on all the bits of the key unless we are sure that all low-order p-bit patterns are equally likely.
    • Research says that the hash function obtained from the division method gives the best results when the size of the table is prime. If table_length is prime and if r is the number of possible character codes on a system such that r % table_length = 1, then h(key) = sum of binary representation of characters in key % table_length.

• Mid square method:

  • Suppose we want to place a record of key 3101 and the size of hash table is 2000.
  • Here, firstly the key is squared and then mid part of the resultant number is taken as the index for the hash table. So in our case: key = 3101 => (3101)² = 3101*3101 = 9616201 i.e.
    h(key) = h(3101) = 162 (by taking middle 3 digit from 9616201). Place the record in 162^nd index of the hash table. 

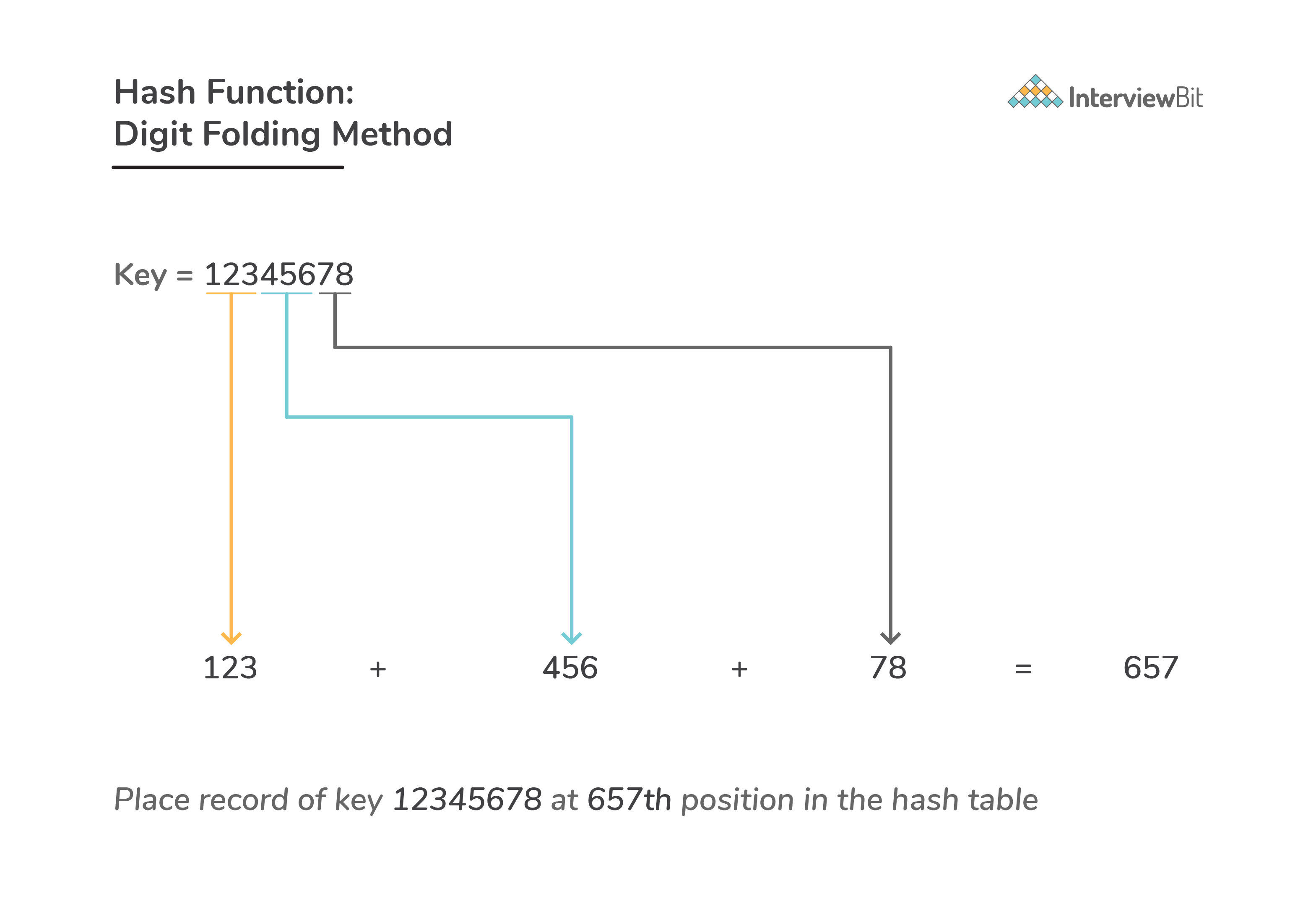
• Digit folding method:

  • Here, the key is divided into separate parts and by using simple operations these separated parts are combined to produce a hash.
  • Consider a record of key 12345678. Divide this into parts say 123, 456, 78. After dividing the parts combine these parts by performing add operation on them. h(key) = h(12345678) = 123 + 456 + 78 = 657 

• Multiplication method:

  • In this method, the hash function implementation is as follows:

    • we multiply key key by a real number c that lies in the range 0 < c < 1 and fractional part of their product is extracted.
    • Then, this fractional part is multiplied by size of hash table table_size. The floor of the result is considered as the final hash. It is represented as

      h(key) = floor (table_size * (key * (c mod 1)))
                           or
      h(key) = floor (table_size * fractional (key * c))
      

      Here, the function floor(x) returns the integer part of the real number x, and fractional(x) yields the fractional part of that number by performing fractional(x) = x – floor(x) 

  • The main advantage of this method is that the value of table size (table_size) doesnt matter. Typically, this value is chosen as a power of 2 since this can be easily implemented on most computing systems.

Collisions

• The phenomenon where two keys generate same hash value from a given hash function is called as a collision. A good hash function should ensure that the collisions are minimum. 
• We will look in details about how to minimise collisions in the next section.

Load Factor:

• The load factor is simply a measure of how full (occupied) the hash table is, and is simply defined as: α = number of occupied slots/total slots
• In simple words, consider we have a hash table of size 1000, and we have 500 slots filled, then the load factor would become α = 500/1000 = 0.5
• Larger the load factor value, larger is the space saved but at the cost of inserting more elements in a slot via chaining (We will learn about chaining in the below sections). This would worsen the access time of elements.
• Generally, whenever a tight situation between deciding what is more important - time or space - we incline towards optimising time (increasing speed) than the memory space. This is called as time-space tradeoff.
  • To optimise the time complexity, we can reduce the load factor, but doing this will increase the memory or space required for hash table.