Selection sort is a simple comparison-based sorting algorithm. It is in-place and needs no extra memory.
The idea behind this algorithm is pretty simple. We divide the array into two parts: sorted and unsorted. The left part is sorted subarray and the right part is unsorted subarray. Initially, sorted subarray is empty and unsorted array is the complete given array.
We perform the steps given below until the unsorted subarray becomes empty:
- Pick the minimum element from the unsorted subarray.
- Swap it with the leftmost element of the unsorted subarray.
- Now the leftmost element of unsorted subarray becomes a part (rightmost) of sorted subarray and will not be a part of unsorted subarray.
A selection sort works as follows:
Part of unsorted array
Part of sorted array
Leftmost element in unsorted array
Minimum element in unsorted array
This is our initial array A = [5, 2, 6, 7, 2, 1, 0, 3]
Leftmost element of unsorted part = A[0]
Minimum element of unsorted part = A[6]
We will swap A[0] and A[6] then, make A[0] part of sorted subarray.
Leftmost element of unsorted part = A[1]
Minimum element of unsorted part = A[5]
We will swap A[1] and A[5] then, make A[1] part of sorted subarray.
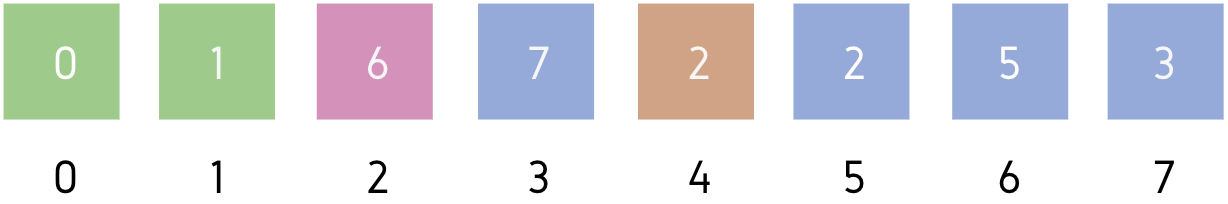
Leftmost element of unsorted part = A[2]
Minimum element of unsorted part = A[4]
We will swap A[2] and A[4] then, make A[2] part of sorted subarray.
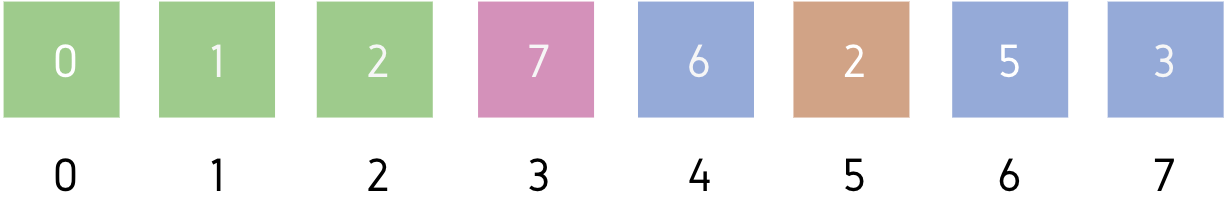
Leftmost element of unsorted part = A[3]
Minimum element of unsorted part = A[5]
We will swap A[3] and A[5] then, make A[3] part of sorted subarray.
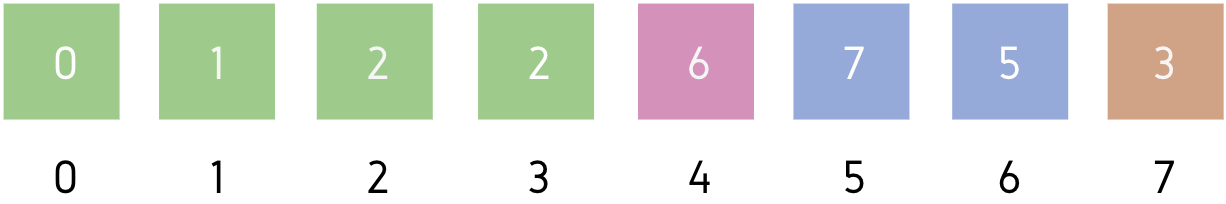
Leftmost element of unsorted part = A[4]
Minimum element of unsorted part = A[7]
We will swap A[4] and A[7] then, make A[4] part of sorted subarray.
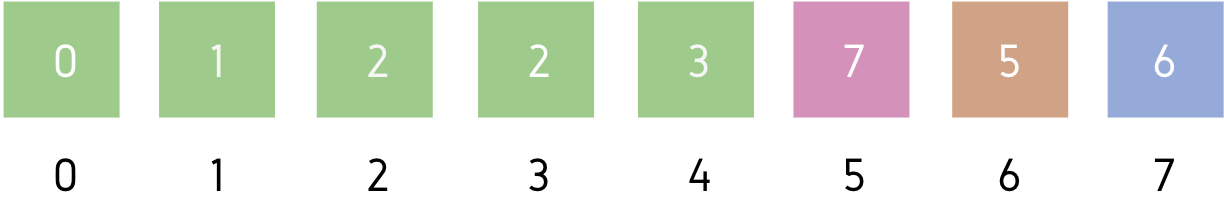
Leftmost element of unsorted part = A[5]
Minimum element of unsorted part = A[6]
We will swap A[5] and A[6] then, make A[5] part of sorted subarray.
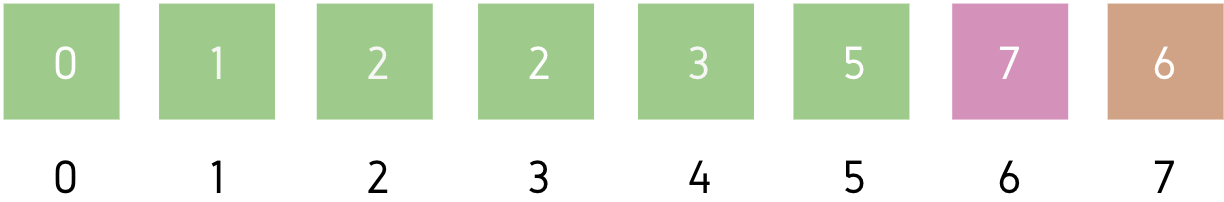
Leftmost element of unsorted part = A[6]
Minimum element of unsorted part = A[7]
We will swap A[6] and A[7] then, make A[6] part of sorted subarray.
This is the final sorted array.
Pseudocode
FindMinIndex:
FindMinIndex(Arr[], start, end)
min_index = start
FOR i from (start + 1) to end:
IF Arr[i] < Arr[min_index]:
min_index = i
END of IF
END of FOR
Return min_indexSuppose, there are ‘n’ elements in the array. Therefore, at worst case, there can be n iterations in FindMinIndex() for start = 1 and end = n. We did not take any auxiliary space.
Therefore,
Time complexity: O(n)
Space complexity: O(1)
Selection Sort:
SelectionSort(Arr[], arr_size):
FOR i from 1 to arr_size:
min_index = FindMinIndex(Arr, i, arr_size)
IF i != min_index:
swap(Arr[i], Arr[min_index])
END of IF
END of FORSuppose, there are ‘n’ elements in the array. Therefore, at worst case, there can be n iterations in FindMinIndex() for start = 1 and end = n. No auxiliary space used.
Total iterations = (n – 1) + (n – 2) + . . . + 1 = (n * (n – 1)) / 2 = (n2 – n) / 2
Therefore,
Time complexity: O(n2)
Space complexity: O(1)
Implementation:
Following are C, C++, Java and Python implementations of Selection Sort.
Selection sort program in C:
#include <stdio.h>
void swap(int *A, int i, int j) {
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
int findMinIndex(int *A, int start, int end) {
int min_index = start;
++start;
while(start < end) {
if(A[start] < A[min_index])
min_index = start;
++start;
}
return min_index;
}
void selectionSort(int *A, int n) {
for(int i = 0; i < n - 1; ++i) {
int min_index = findMinIndex(A, i, n);
if(i != min_index)
swap(A, i, min_index);
}
}
int main() {
int A[] = {5, 2, 6, 7, 2, 1, 0, 3}, n = 8;
selectionSort(A, n);
for(int i = 0; i < n; ++i)
printf("%d ", A[i]);
return 0;
}Selection sort program in C++:
#include <iostream>
#include <vector>
using namespace std;
int findMinIndex(vector<int> &A, int start) {
int min_index = start;
++start;
while(start < (int)A.size()) {
if(A[start] < A[min_index])
min_index = start;
++start;
}
return min_index;
}
void selectionSort(vector<int> &A) {
for(int i = 0; i < (int)A.size(); ++i) {
int min_index = findMinIndex(A, i);
if(i != min_index)
swap(A[i], A[min_index]);
}
}
int main() {
vector<int> A = {5, 2, 6, 7, 2, 1, 0, 3};
selectionSort(A);
for(int num : A)
cout << num << ' ';
return 0;
} Selection Sort Program in Java
class SelectionSort {
void swap(int A[], int i, int j) {
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
int findMinIndex(int A[], int start) {
int min_index = start;
++start;
while(start < A.length) {
if(A[start] < A[min_index])
min_index = start;
++start;
}
return min_index;
}
void selectionSort(int A[]) {
for(int i = 0; i < A.length; ++i) {
int min_index = findMinIndex(A, i);
if(i != min_index)
swap(A, i, min_index);
}
}
public static void main(String[] args) {
int A[] = {5, 2, 6, 7, 2, 1, 0, 3};
selectionSort(A);
for(int num : A)
System.out.print(num + " ");
return 0;
}
}Selection Sort Program in Python
def findMinIndex(A, start):
min_index = start
start += 1
while start < len(A):
if A[start] < A[min_index]:
min_index = start
start += 1
return min_index
def selectionSort(A):
i = 0
while i < len(A):
min_index = findMinIndex(A, i)
if i != min_index:
A[i], A[min_index] = A[min_index], A[i]
i += 1
A = [5, 2, 6, 7, 2, 1, 0, 3]
selectionSort(A)
for num in A:
print(num, end=' ')
Video Courses
