Bubble sort, also referred to as comparison sort, is a simple sorting algorithm that repeatedly goes through the list, compares adjacent elements and swaps them if they are in the wrong order. This is the most simplest algorithm and inefficient at the same time. Yet, it is very much necessary to learn about it as it represents the basic foundations of sorting.

Table of Content

1. Application
2. Explanation
3. Bubble Sort Example
4. Pseudocode of Bubble sort algorithm
5. Implementation of Bubble Sort algorithm
6. Complexity Analysis
7. FAQs

Application

Understand the working of Bubble sort

• Bubble sort is mainly used in educational purposes for helping students understand the foundations of sorting.
• This is used to identify whether the list is already sorted. When the list is already sorted (which is the best-case scenario), the complexity of bubble sort is only O(n).
• In real life, bubble sort can be visualised when people in a queue wanting to be standing in a height wise sorted manner swap their positions among themselves until everyone is standing based on increasing order of heights.

Explanation

Algorithm: We compare adjacent elements and see if their order is wrong (i.e a[i] > a[j] for 1 <= i < j <= size of array; if array is to be in ascending order, and vice-versa). If yes, then swap them.

Explanation:

• Let us say, we have an array of length n. To sort this array we do the above step (swapping) for n - 1 passes.
• In simple terms, first, the largest element goes at its extreme right place then, second largest to the last by one place, and so on. In the ith pass, the ith largest element goes at its right place in the array by swappings.
• In mathematical terms, in ith pass, at least one element from (n - i + 1) elements from start will go at its right place. That element will be the ith (for 1 <= i <= n - 1) largest element of the array. Because in the ith pass of the array, in the jth iteration (for 1 <= j <= n - i), we are checking if a[j] > a[j + 1], and a[j] will always be greater than a[j + 1] when it is the largest element in range [1, n - i + 1]. Now we will swap it. This will continue until ith largest element is at the (n - i + 1)th position of the array.

Bubble Sort Example:

Consider the following array: Arr=14, 33, 27, 35, 10. We need to sort this array using bubble sort algorithm.

First Pass:

• We proceed with the first and second element i.e., Arr[0] and Arr[1]. Check if 14 > 33 which is false. So, no swapping happens and the array remains the same.

• We proceed with the second and third element i.e., Arr[1] and Arr[2]. Check if 33 > 27 which is true. So, we swap Arr[1] and Arr[2].

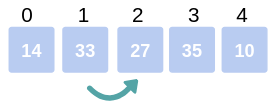
Thus the array becomes: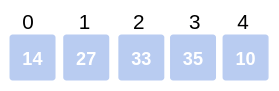

• We proceed with the third and fourth element i.e., Arr[2] and Arr[3]. Check if 33 > 35 which is false. So, no swapping happens and the array remains the same.

• We proceed with the fourth and fifth element i.e., Arr[3] and Arr[4]. Check if 35 > 10 which is true. So, we swap Arr[3] and Arr[4].

Thus, after swapping the array becomes: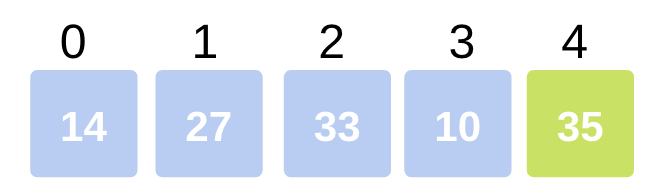

Thus, marks the end of the first pass, where the Largest element reaches its final(last) position.

Second Pass:

• We proceed with the first and second element i.e., Arr[0] and Arr[1]. Check if 14 > 27 which is false. So, no swapping happens and the array remains the same.

We now proceed with the second and third element i.e., Arr[1] and Arr[2]. Check if 27 > 33 which is false. So, no swapping happens and the array remains the same.

• We now proceed with the third and fourth element i.e., Arr[2] and Arr[3]. Check if 33 > 10 which is true. So, we swap Arr[2] and Arr[3].

Now, the array becomes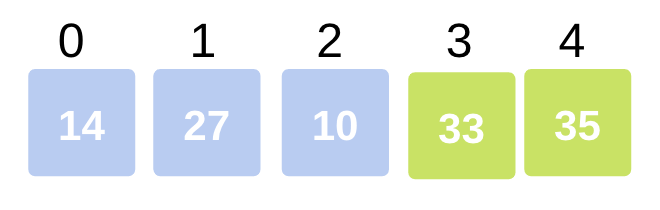

Thus marks the end of second pass where the second largest element in the array has occupied its correct position.

Third Pass:
After the third pass, the third largest element will be at the third last position in the array.

.

.

i-th Pass:
After the ith pass, the ith largest element will be at the ith last position in the array.

.

.
n-th Pass:
After the nth pass, the nth largest element(smallest element) will be at nth last position(1st position) in the array, where ‘n’ is the size of the array.

After doing all the passes, we can easily see the array will be sorted.
Thus, the sorted array will look like this:

Pseudocode of Bubble Sort Algorithm

bubbleSort( Arr[], totat_elements)
   
   for i = 0 to total_elements - 1 do:
      swapped = false
		
      for j = 0 to total_elements - i - 2 do:
      
         /* compare the adjacent elements */   
         if Arr[j] > Arr[j+1] then
            /* swap them */
            swap(Arr[j], Arr[j+1])		 
            swapped = true
         end if
         
      end for
      
      /*if no number was swapped that means 
      array is sorted now, break the loop.*/
      
      if(not swapped) then
         break
      end if
      
   end for
   
end

Implementation Of Bubble Sort

Implementation of bubble sort in C
#include<stdio.h>
 
int main()
{
   int arr[] = {5, 6, 2 ,6, 9, 0, -1}, n = 7, i, j;
   
   for(i = 0; i < n - 1; ++i)
   { 
      int swapped = 0;

      for(j = 0; j < (n - i - 1); ++j)
         if(arr[j] > arr[j+1])
         {
            int temp = arr[j];
            arr[j] = arr[j+1];
            arr[j+1] = temp;

            swapped = 1;
         }
      if(!swapped)
         break;
   }
         
   printf("\nArray after sorting: ");
   for(i = 0; i < n; ++i)
      printf("%d ", arr[i]);
 
   return 0;
}

Implementation of Bubble sort in C++
#include <iostream>
#include <vector>
 
using namespace std;
 
void BubbleSort (vector<int> &arr, int n)
{
   for (int i = 0; i < n - 1; ++i)
   { 
      bool swapped = false;
      for (int j = 0; j < n - i - 1; ++j)
      {
         if (arr[j] > arr[j+1]) //check if adjacent element is
                      //not in order
         {
            swap(arr[j], arr[j + 1]);
            swapped = true;
         }
      }
      // Value at n-i-1 will be maximum of all the values below this index.

      if(!swapped)
         break;
   } 
} 
 
int main()
{
   vector<int> arr = {5, 6, 2, 6, 9, 0, -1};
   int n = 7;
 
   BubbleSort(arr, n);
 
   // Display the sorted data.
   cout << "\nSorted Data: ";
   for (i = 0; i < n; i++)
        Cout << arr[i] << “ “;
 
   return 0;
}

Implementation of Bubble Sort in Java:
import java.util.Scanner;
class BubbleSort {
  public static void main(String []args) {
    int n;
    Scanner in = new Scanner(System.in);
 System.out.println("Input number of integers to sort");
    n = in.nextInt();
    int array[] = new int[n];
     System.out.println("Enter " + n + " integers");
     for (int i = 0; i < n; i++)
      array[i] = in.nextInt();
   
    for (int i = 0; i < n - 1; i++) {
   Boolean swapped = false;
      for (int j = 0; j < n - i - 1; j++) {
        if (array[j] > array[j+1]) /* For descending order use < */
        {
          int temp = array[j];
          array[j]= array[j+1];
          array[j+1] = temp;

      swapped = true;
        }
      }
   if(!swapped)
      break;
   } 
System.out.println("Sorted list of numbers:");
for (int i = 0; i < n; i++)
System.out.println(array[i]);
  }
}

Implementation of bubble sort in python
def bubble_sort(arr):
    for i in range(len(arr) - 1):
        swapped = False
        for j in range(0, len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swapped = True
        if not swapped:
            return
 
 
arr = [int(x) for x in input(‘Enter numbers: ’).split()]
bubble_sort(arr)
print('Sorted list: ', end='')
print(arr)

Complexity Analysis

Time Complexity of Bubble sort

• Best case scenario: The best case scenario occurs when the array is already sorted. In this case, no swapping will happen in the first iteration (The swapped variable will be false). So, when this happens, we break from the loop after the very first iteration. Hence, time complexity in the best case scenario is O(n) because it has to traverse through all the elements once.
• Worst case and Average case scenario: In Bubble Sort, n-1 comparisons are done in the 1st pass, n-2 in 2nd pass, n-3 in 3rd pass and so on. So, the total number of comparisons will be:

  Sum = (n-1) + (n-2) + (n-3) + ..... + 3 + 2 + 1 
  Sum = n(n-1)/2
  

  Hence, the time complexity is of the order n² or O(n²).

Space Complexity of Bubble sort

The space complexity for the algorithm is O(1), because only a single additional memory space is required i.e. for temporary variable used for swapping.

FAQs

• What is the best case time complexity of bubble sort?
  The time complexity in the best case scenario is O(n) because it has to traverse through all the elements once to recognize that the array is already sorted.

• What is the advantage of bubble sort over other sorting techniques?

  • The built-in ability to detect whether the list is sorted efficiently is the only advantage of bubble sort over other sorting techniques.
  • When the list is already sorted (which is the best-case scenario), the complexity of bubble sort is only O(n).
  • It is faster than other in case of sorted array and consumes less time to describe whether the input array is sorted or not.

• Why bubble sort is called “bubble” sort?
  The “bubble” sort is called so because the list elements with greater value than their surrounding elements “bubble” towards the end of the list. For example, after first pass, the largest element is bubbled towards the right most position. After second pass, the second largest element is bubbled towards the second last position in the list and so on.

• Is bubble sort a stable algorithm?

  • Bubble sort is a stable algorithm.
  • A sorting algorithm is said to be stable if two objects with equal keys appear in the same order in sorted output as they appear in the input array to be sorted.

• Is bubble sort an inplace algorithm?

  • Bubble sort is an inplace algorithm.
  • An algorithm is said to be inplace if it does not need an extra space and produces an output in the same memory that contains the data by transforming the input ‘in-place’. However, a small constant extra space used for variables is allowed.

• Is Bubble sort slow?

  • Bubble sort is slower than the other O(n²) sorting algorithms.
  • It is about four times as slow as insertion sort and twice as slow as selection sort.
  • It has a good best-case behavior, but is impractically slow on almost all real world data sets and is not considered for implementation in real applications.

• Can bubble sort be implemented recursively?

  • Yes.
  • Recursive Bubble Sort has no additional performance/implementation advantages, but can be used to understand recursion and sorting concepts better.
  • Base Case: If array size is 1, return.
  • Do One Pass of normal Bubble Sort. This pass bubbles largest element of current subarray to correct position.
  • Recur for all elements except last of current subarray.

    recursiveBubbleSort(arr[], n){
        // Base case
        if (n == 1)
        return;

        // One pass of bubble sort. After
        // this pass, the largest element
        // is moved (or bubbled) to end.
        for(i=0; i<n-1; i++){
            if(arr[i] > arr[i+1])
            {
             swap(arr[i], arr[i+1]);
            }
        }

        // recursion for remaining elements in array
        recursiveBubbleSort(arr, n-1);
    }